コンパスを使って、平行四辺形を作図する方法について解説していきます。
下の図のように2つの辺がある状態から、平行四辺形を作図してみましょう!
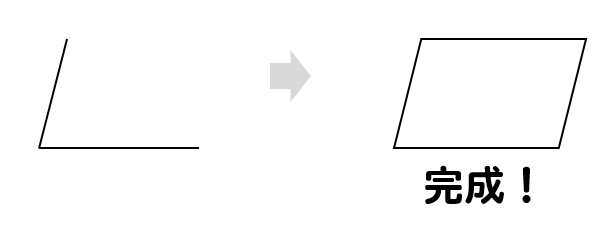
【平行四辺形の書き方】コンパスを使って作図する方法は?
説明がしやすいように頂点にA,B,Cと名前をつけておきますね。
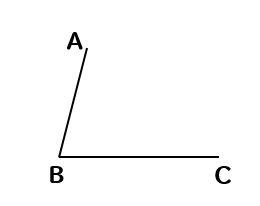
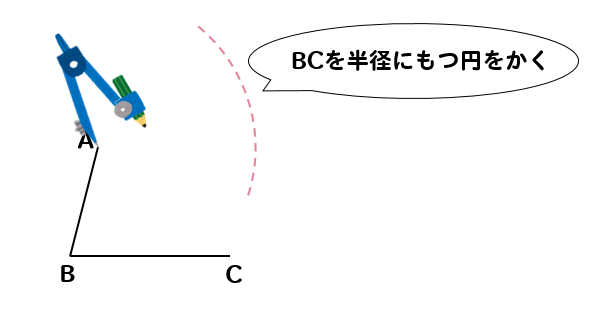
まずは、コンパスを辺BCの長さに合わせます。
その長さを取ったまま、点Aにコンパスの針を置き、円を書きます。
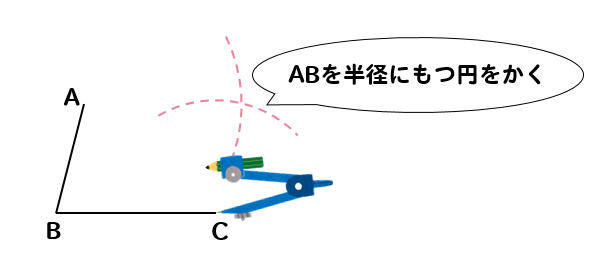
次に、コンパスを辺ABの長さに合わせます。
その長さを取ったまま、点Cにコンパスの針を置き、円を書きます。
すると、コンパスで作図した2つの円に交わるところができます。
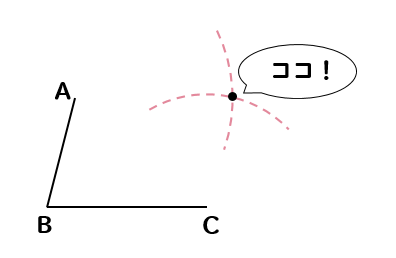
これに対して、線を結んでいけば平行四辺形の完成です!
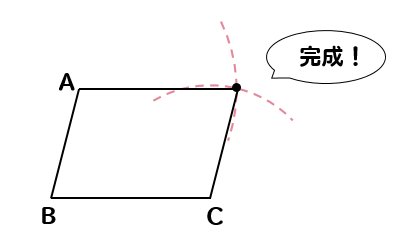
【平行四辺形の書き方】なぜ?
上の章では、平行四辺形の書き方の手順について解説しました。
やり方としては、とっても簡単でしたね!
だけど、なんでこんなやり方でできるの?と疑問に思った方もいるでしょう。
というわけで、簡単ではありますが平行四辺形の書き方のなぜ?について触れておきます。
まず、平行四辺形の性質を覚えておきましょう。
四角形は次の条件を満たすと、平行四辺形になります。
【平行四辺形になるための条件】
- 2組の対辺がそれぞれ平行である。
- 2組の対辺がそれぞれ等しい。
- 2組の対角がそれぞれ等しい。
- 対角線がそれぞれの中点で交わる。
- 1組の対辺が平行でその長さがそれぞれ等しい。
この条件の中から、「2組の対辺がそれぞれ等しい」という条件を使って作図をしています。
まず、BCと同じ長さを半径に持つ円を書くことで
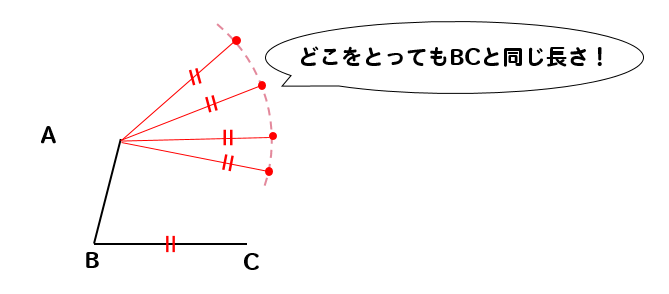
このように、点AからBCと同じ長さになる場所を調べることができます。
同じように、ABと同じ長さを半径に持つ円を書くことで
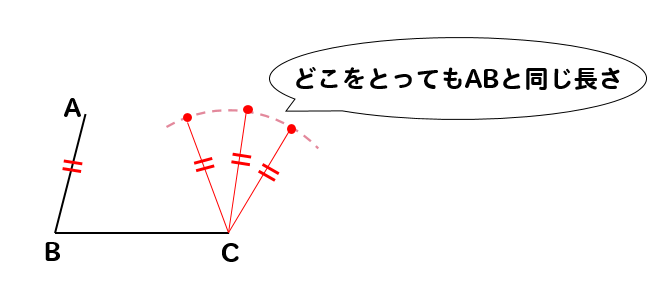
このように点CからABと同じ長さになる場所を調べることができます。
そして、それらが交わる場所
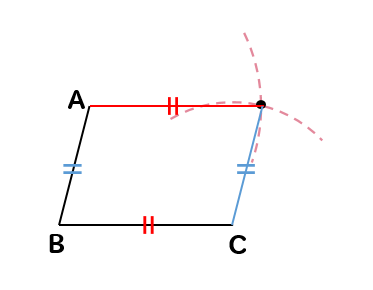
これが2組の対辺がそれぞれ等しくなる場所!というわけですね。
【平行四辺形の書き方】まとめ!
お疲れ様でした!
最後に手順をおさらいしておきましょう。



今回の平行四辺形の書き方は、のちに学習するであろう高校数学の作図にも役立ちます。
なので、しっかりと覚えておきたいですね(^^)
















コメント失礼します
【平行四辺形の書き方】まとめ!
の部分の、
「ACを半径にもつ円をかく」というのは、
「BCを半径にもつ円をかく」が正しいのではないでしょうか?
ミスってました…(^^;)
ご指摘ありがとございました!