今回はコンパスを使って円の接線を作図する方法について解説していくよ!
中学で学習する基本的な作図から
2つの円に接する超難問の作図まで解説していきます!
この記事では接線のかき方をメインにお伝えしていますが、記事の途中に発展的な「接線の性質を活用した作図」についての演習も用意しています。
これによってグッと応用力が高まってくるので、あわせてご活用くださいね^^
円の接線とは
円の接線を作図するためには、接線の特徴を知っておく必要があります。
大事な性質はコレ!
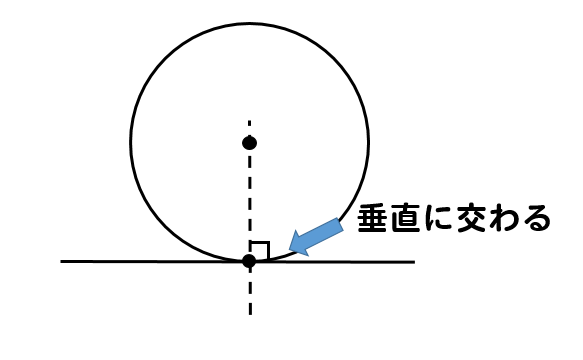
中心と接点を結んだ線は、接線と垂直に交わります。
つまり、垂線の作図を用いることで接線を完成させていくことになります。
円の接線作図~基本~
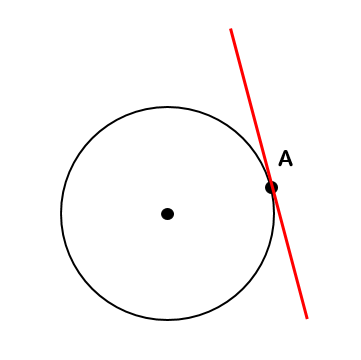
点Aを通るような円の接線を作図しなさい。
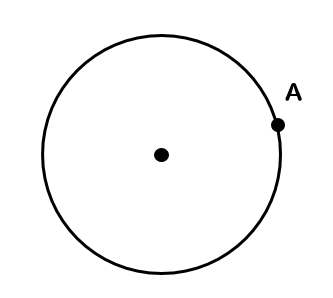
まずは円の中心と接点となる点Aを線で結びましょう。
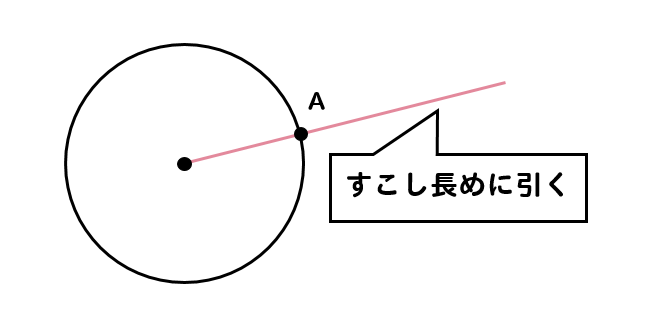
すこしはみ出すように長めに書いてくださいね。
そして、この線に対して点Aを通るような垂線を引いていきます。
点Aにコンパスの針をおいて、適当な長さで円をかきましょう。
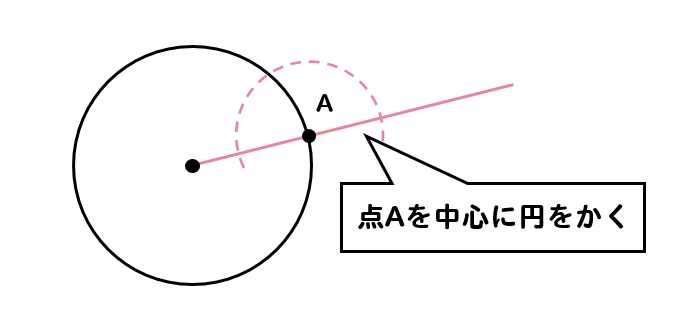
その円がぶつかった2点から、同じ半径を持つ円を2つかきます。
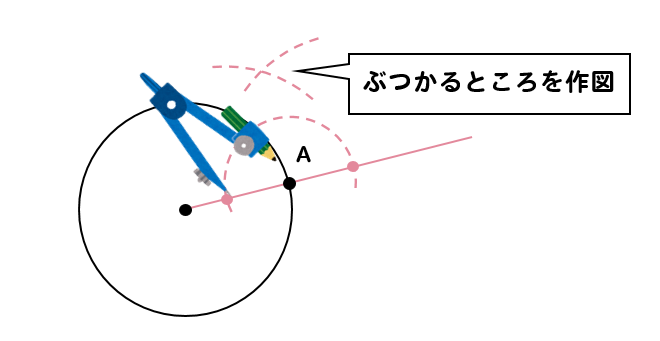
最後に、2つの円がぶつかったところと点Aを結べば完成です!
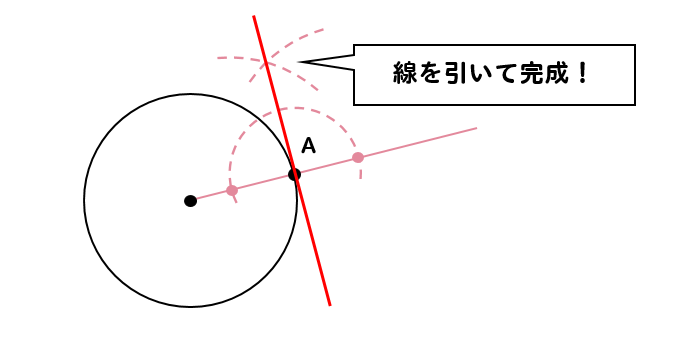
円の接線作図手順
- 中心と接点を結ぶ線を引く
- 接点を通るような垂線を作図
- 完成!
円の接線作図~ある点を通る~
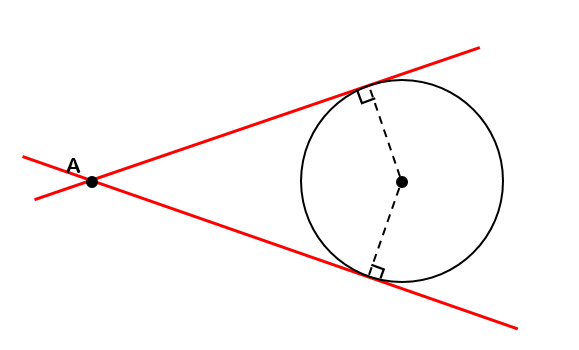
点Aを通るような円の接線を作図しなさい。
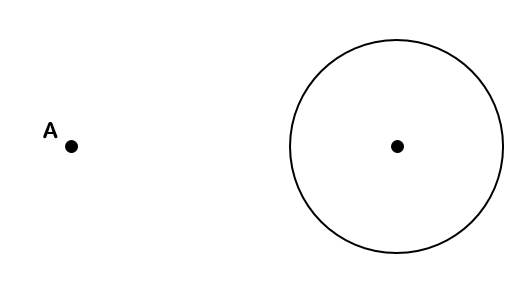
点Aが円の外側にありますね。
こういう場合には完成イメージ図は
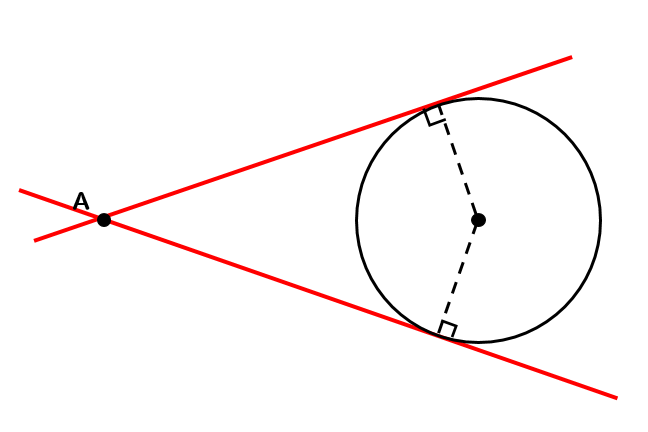
こんな感じになります。
まずは、点Aと円の中心を線で結びます。
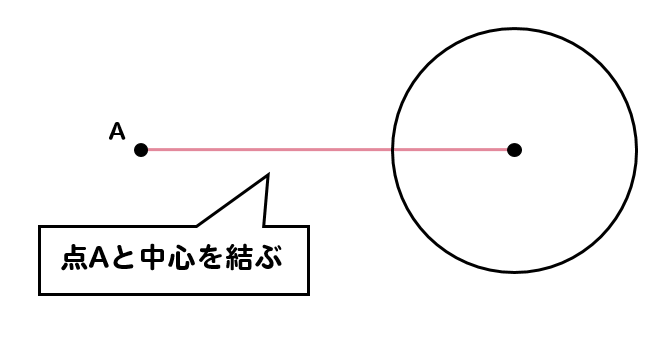
そして、点Aと中心の中点を求めるべく垂直二等分線の作図をします。
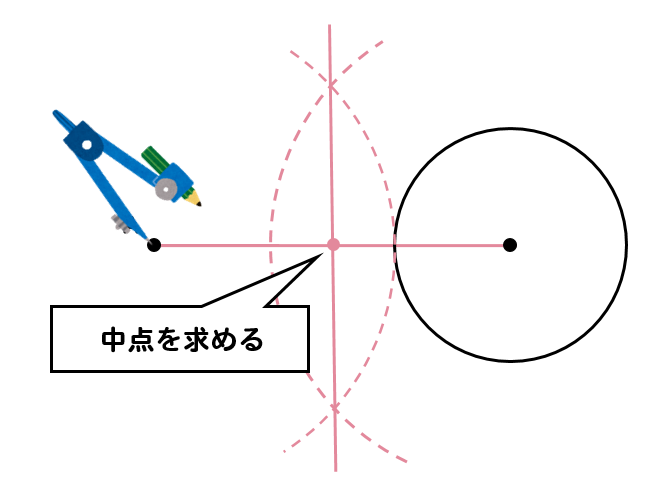
その中点にコンパスの針を置き、点Aと中心の2点を通るような円をかきます。
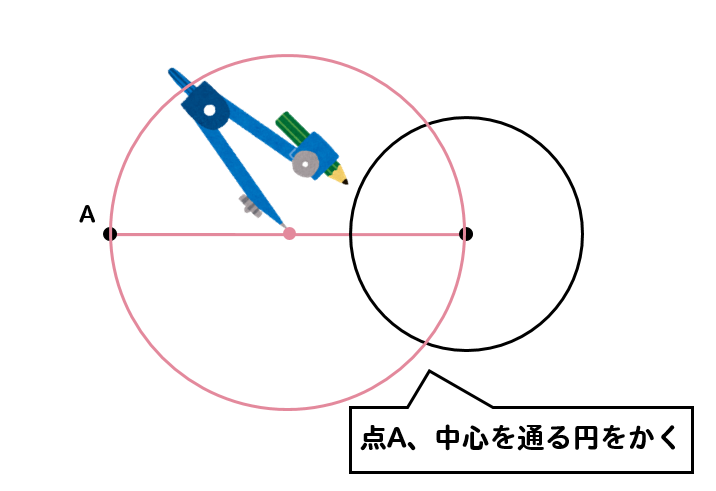
すると、元の円と新たに作図した円とが交わる点が2点できるはずです。
その交点と点Aを結ぶと接線が完成します!
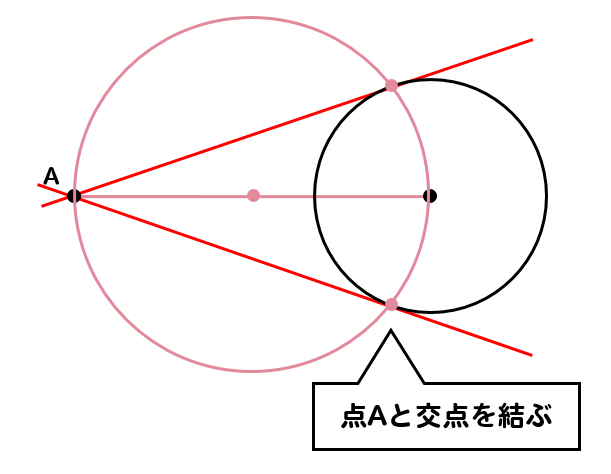
できあがり!!
しかし、これでなぜ接線が引けたことになるのか…
それには円周角の定理というものが関係しています。
詳しくはこちらの記事をご参考ください。
円周角の定理から
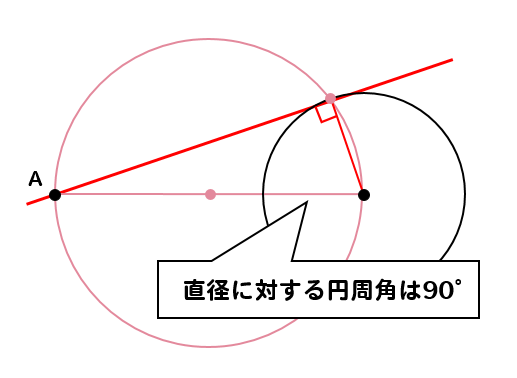
ここの部分が90度になるということが分かるんだ。
ということは、ちゃんと接線の特徴を満たしているってことが分かるよね(^^)
ある点を通る円の接線作図手順
- 点Aと円の中心との中点を作図
- 1の点を中心とする点A、円の中心を通る円を作図
- 元の円と作図した円との交点を2つ求める
- 3の点と点Aを結ぶ
- 完成!
入試によく出る!接線の性質を利用した発展演習2選
さて、ここまでの内容で「接線を作図する」ということはバッチリです!
ですが、入試ではもっと踏み込んで「接線の性質を利用した作図」というものが出題されます。
ん、どういうこと??
と感じた方もいると思うので、今回は接線を利用した発展作図を2題用意しました!
これが理解できれば入試の作図も大丈夫!接線はお任せあれ~♪
といった感じになれますよ^^
① たった2題で接線の応用をクリアさせる厳選問題
② 知ってると図形の見え方が変わってくる!応用力が伸びてくる接線の特徴とは?
③ 2つの接線がでてきたら、〇〇に注目するだけでかんたんに解けちゃう!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます。
手を動かして作図を体験することで「テストでできる!」を実感することができますよ^^
こちらから今すぐチャレンジしてみよう!
円の接線作図~2つの円に接する共通接線~
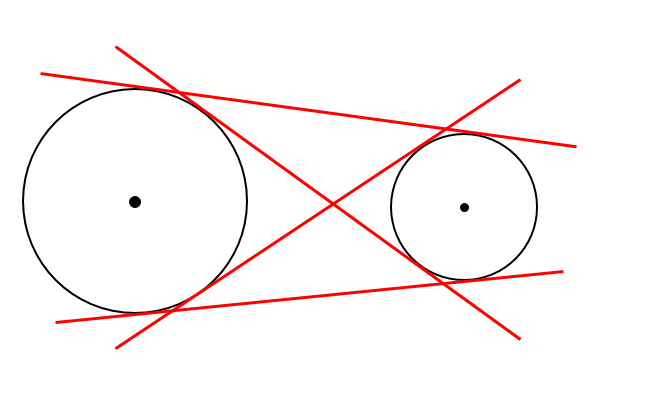
2つの円に対する接線を作図しなさい。
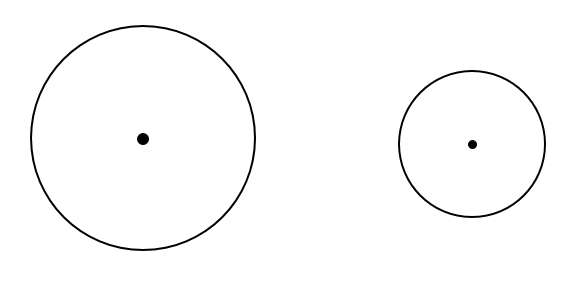
この問題はかなり難しい!
中学生のレベルを超えた内容になるかもしれないから、興味のある方だけ見ていってください。
完成イメージ図はこんな感じです。

1本目の作図方法
まずは、この接線の作図を考えていきます。
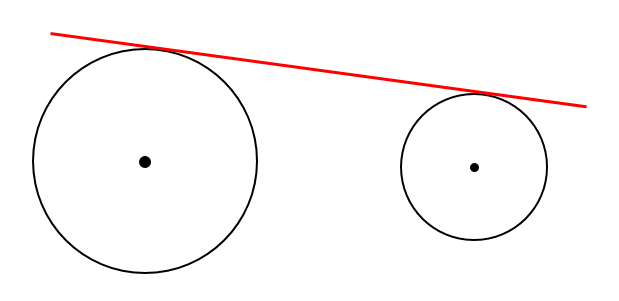
まずは、2円の接線に関する特徴をおさえておきましょう。
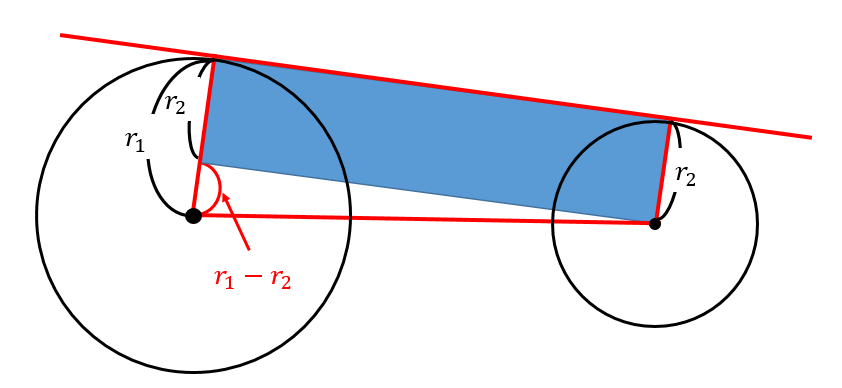
このように補助線を引くと、それぞれの長さが上の図のようになります。
いきなり接線を作図することは難しいです。
そのため、まずは
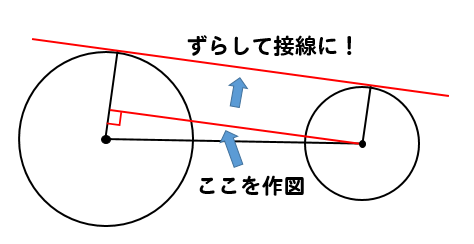
ここの部分を作図し、それを上にずらす形で接線にしていきます。
では、作図開始だ!
まずは2円の中心を結び、それぞれの中点を作図します。
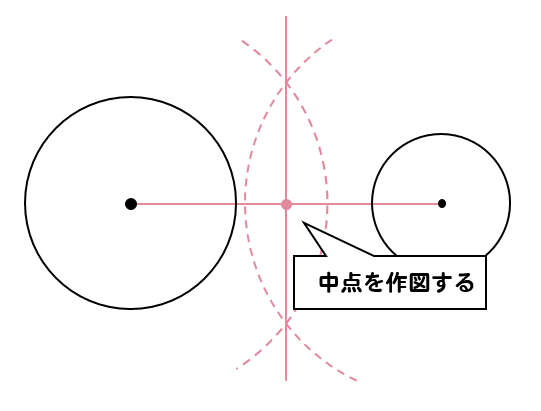
その中点を中心にし、2円の中心を通るような円を作図します。
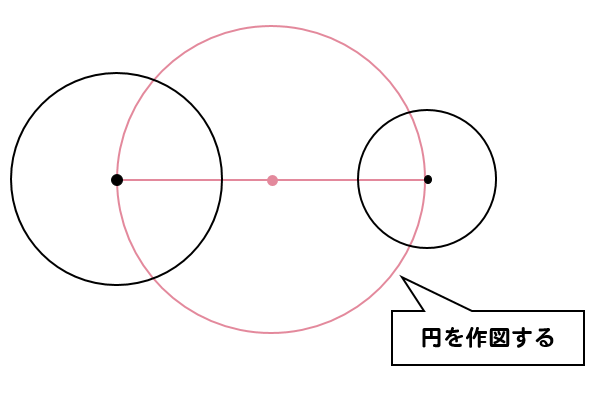
次に小さい方の円の半径をコンパスでとり
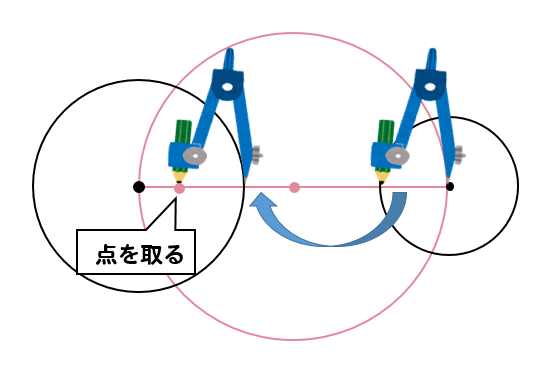
上の図のように点をとります。
すると、このような長さ関係が出来上がります。
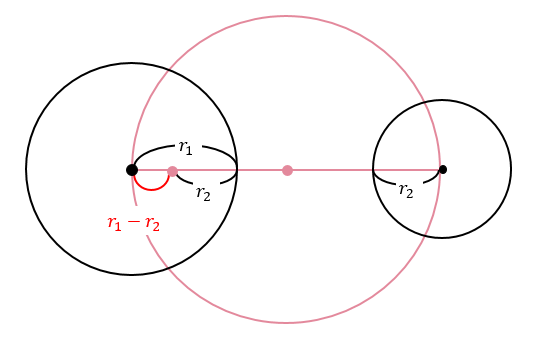
そして、この\(r_1-r_2\)を半径に持つ円をかきます。
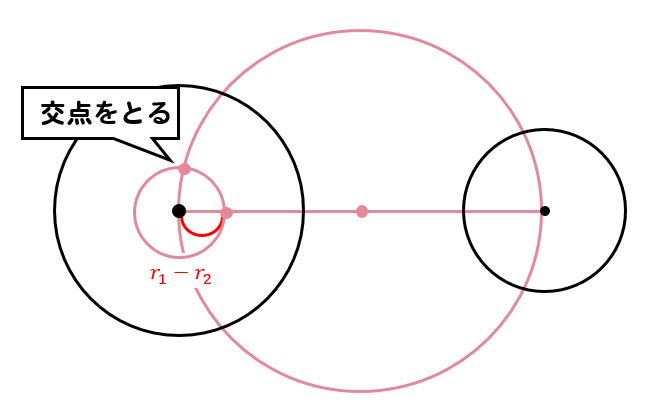
そして、作図された2つの円の交点を取り、小さい円の中心と線で結びます。
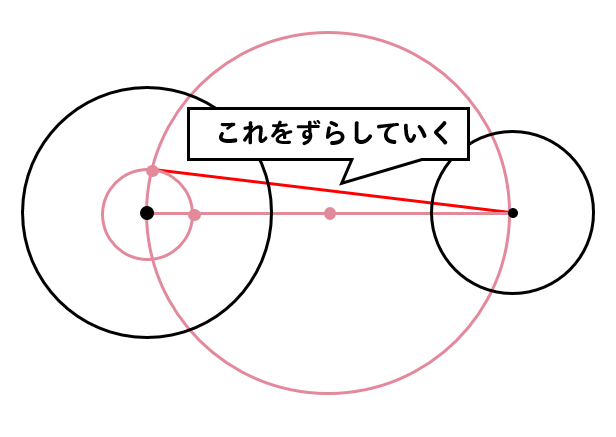
これで、まず目標としていた線を作図することができました。
あとはこの線を上にずらし、接線にしていきます。
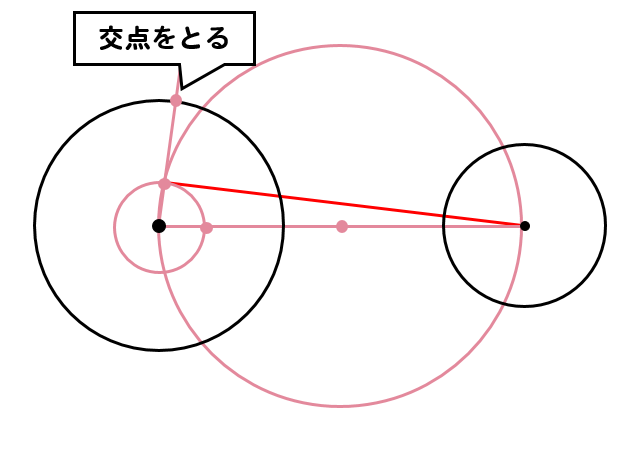
円の中心から先ほど取った点へ線を伸ばし、ぶつかったところに点を取ります。
次に先ほど作図した赤い線の長さをコンパスでとり
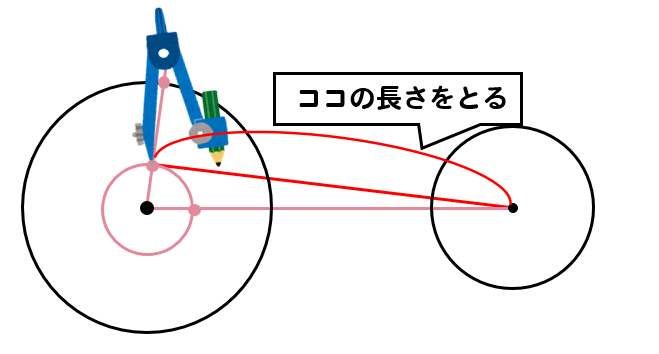
このように点を取ります。
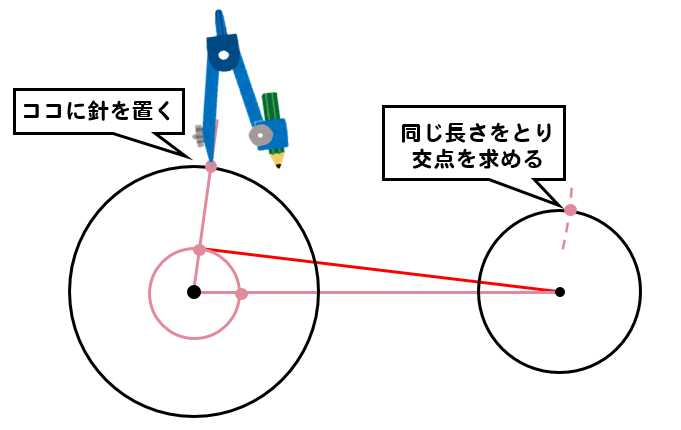
最後にそれぞれの点を結べば完成です!
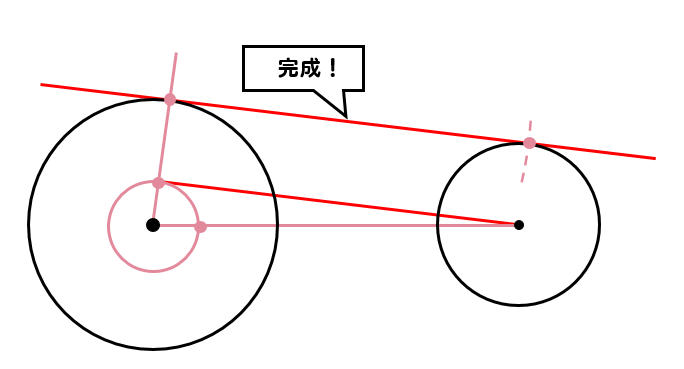
んー、大変だ(^^;)
2本目の作図方法
次はこちらの接線を考えていきましょう。
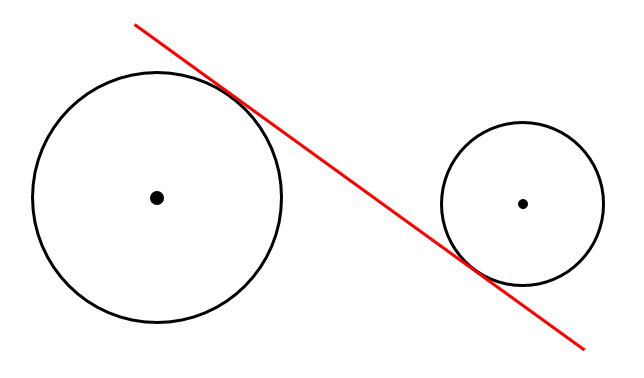
この接線を考える場合には、2円に次のような特徴があることを覚えておきましょう。
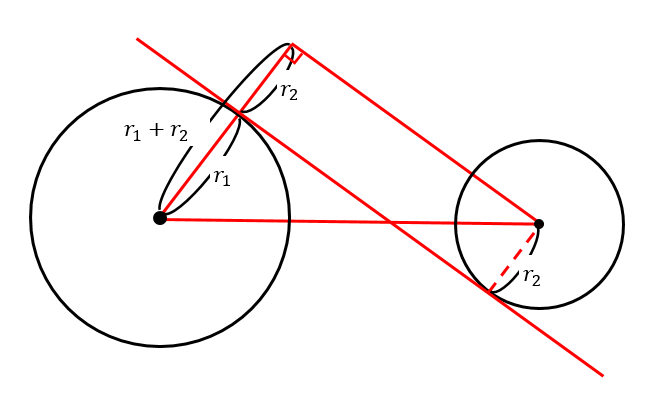
先ほどの接線の作図を理解できれば、こちらも同じような考え方で進めていきます。
まずはそれぞれの中心を通るような円をかきます。
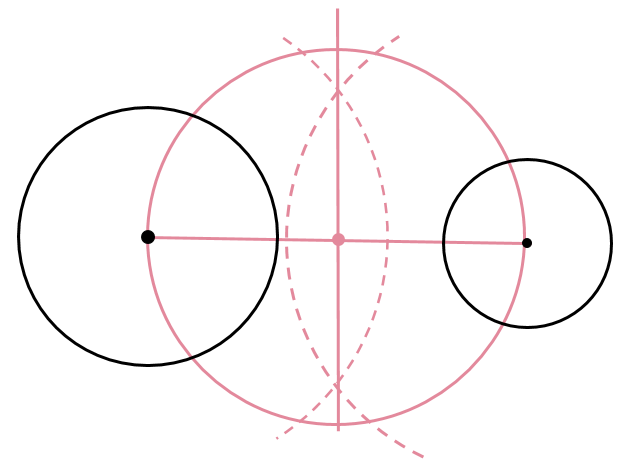
その後、半径\(r_1+r_2\)となるような円をかきます。
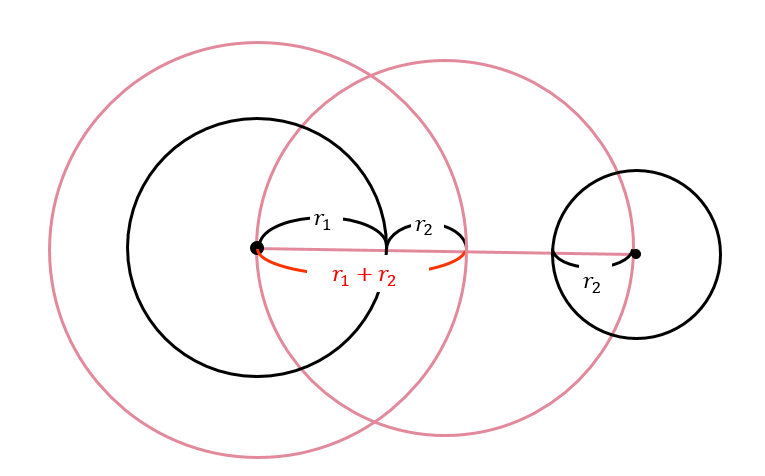
そして、作図した2つの円が交わるとことと小さい円の中心を線で結びます。
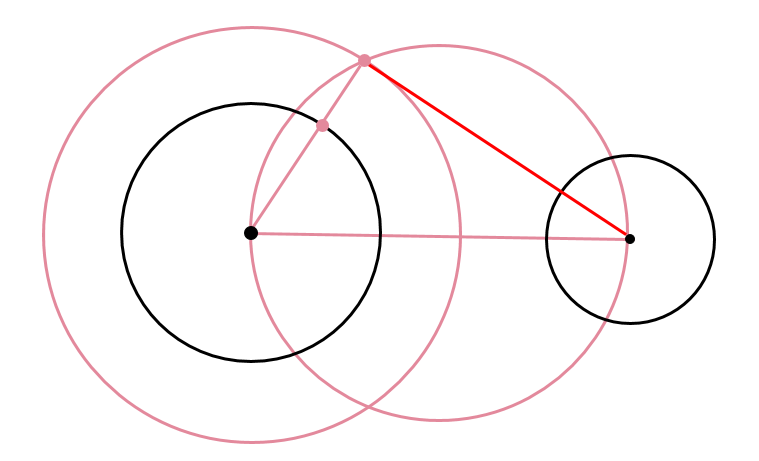
あとは、赤い線と同じ長さをコンパスでとり、線をずらしていきましょう。
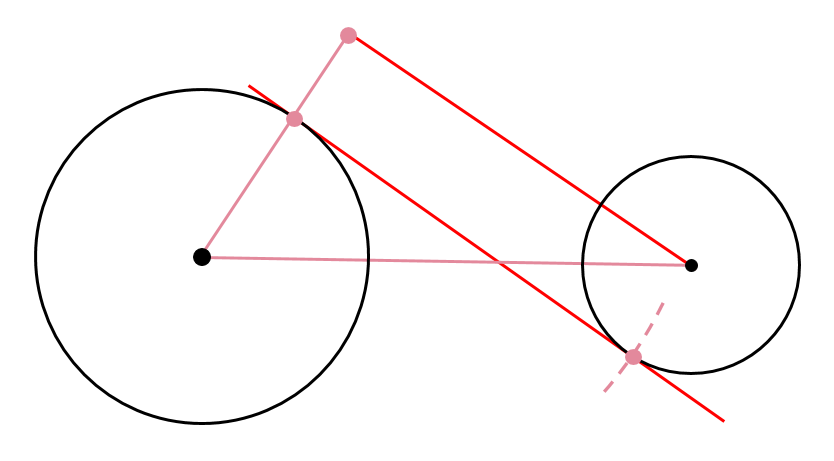
これで完成です!
他の2本に関しては同じようにできますね(^^)
円の接線作図 まとめ
お疲れ様でした!
中学生が入試レベルで学習しておきたいのは


この2つですね!
これは入試問題として出題されることもあるので、しっかりとマスターしておきましょう。
2つの円の共通接線は難しかったね(^^;)
あまり問われることはないと思うんだけど、やり方を頭に入れておくと知識としての引き出しが広がって賢くなるかもね!
ということで、今回はこれで終わり(/・ω・)/
















めっちゃわかりやすい!
数学はテストがあって
作図の問題(特に円)があって
滅茶苦茶不安だったけど
今回のサイトを見て自信が持てました!
今後分からない事があれば
愛用させて頂きます!
テストで良い点取ってきます!
この記事の解説を作るの大変だったので、
そう言ってもらえるとすごく嬉しいです(^^)
テストがんばってください!
中学2年です。
2円の接線を作図する問題が期末テストに出そうなので参考になりました!ありがとうございます。
2円の接線、マジで難しいですよね(^^;)
これがテストに出るなんて…
でもお役に立てたのであれば嬉しいです^^
テストファイト!
明日図形のテストなのによくわからなかったので本当に助かりました!
ありがとうございます!
明日のテストがんばってね!!
今日出ました!
わかりやすくて助かりました!