今回は中2で学習する『平行線と線分』という単元から
等積変形という問題を解説していきます。
等積変形というのは
面積の等しい三角形を見つける問題や
面積が等しくなるように図形を変形する問題です。
まずは、等積変形をやっていく上で
とっても大切な基礎の部分を学習しておきましょう。
今回の内容はこちらの動画でも解説しています!
サクッと理解したい方は動画がおススメ(‘ω’)ノ
等積変形の基本性質
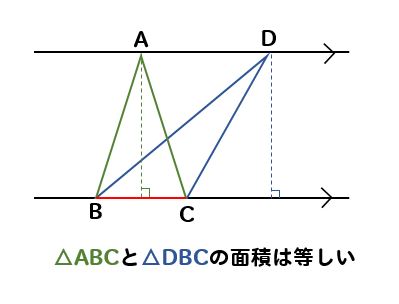
平行な線に挟まれている三角形は、底辺の大きさが等しければ面積が等しくなる。
これが、平行線と面積に関する基本性質です。
でも、なんで面積が等しくなるの??

それはね!
平行線は、どこを取っても距離が等しくなるよね。
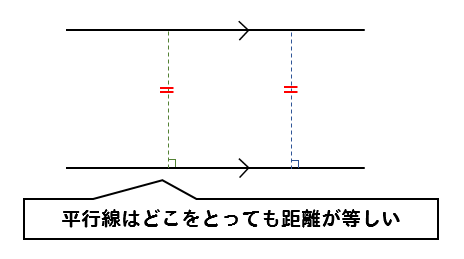
だから、平行線に挟まれている三角形は
どれも高さが等しいということになるんだ。
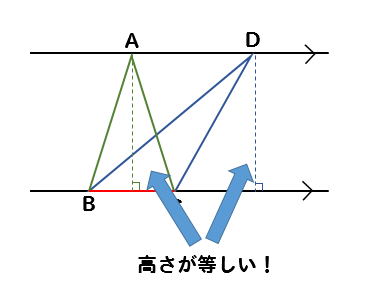
三角形の面積は
$$(底辺)\times (高さ)\times \frac{1}{2}$$
で求めることができるので
底辺、高さがそれぞれ等しくなる三角形は
面積も等しくなるよね!っていう話です。
だから
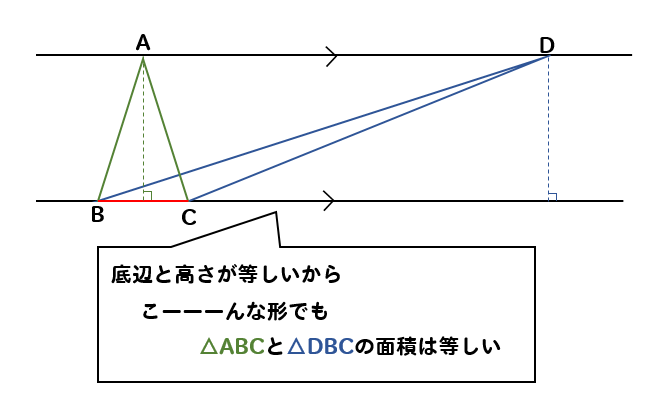
こーーんな形の三角形であっても
底辺と高さが同じになっているので面積は等しいということになります。
あ!
底辺は、こうやって離れていても
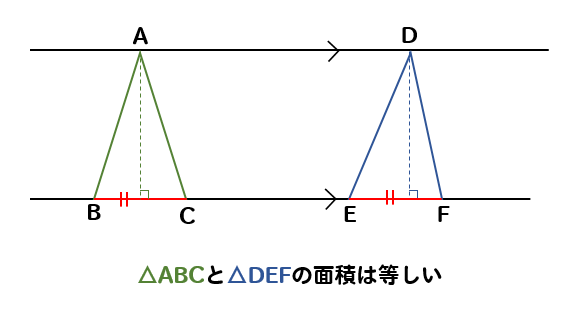
長さが等しければ、面積は等しくなるからね!
ポイントは
平行線に挟まれている三角形は高さが等しい!
というところです。
それでは、この性質を利用していろんな問題を解説していきますね。
台形の中から等しい三角形を見つける問題
下の図で、AD//BCであるとき、面積の等しい三角形の組をすべてみつけ、そのことを記号を使って表しなさい。
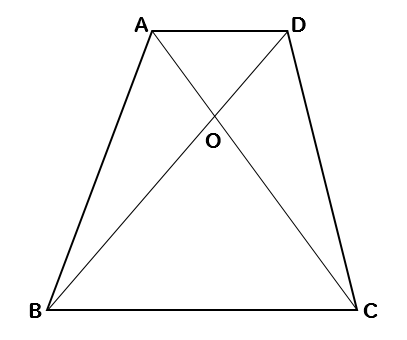
それでは、平行線と面積の性質を利用して考えていきましょう。
AD//BCを利用して、底辺をBCとして考えると
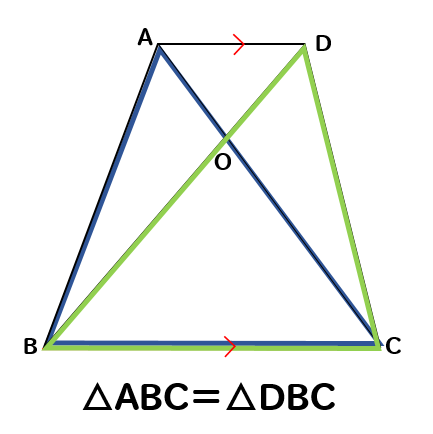
△ABC=△DBCとなります。
それぞれ底辺と高さが等しくなっているから面積も等しくなるね。
次は底辺をADとして考えると
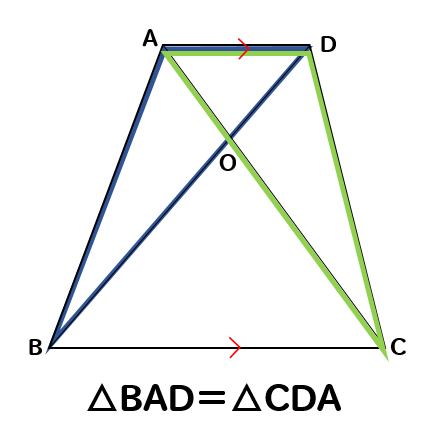
△BAD=△CDAとなります。
そして、最後に
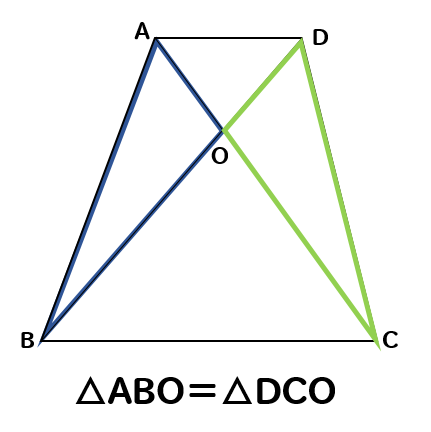
△ABOと△DCOも面積が等しくなります。
え…!?
この2つの三角形は、平行な線に挟まれていないのに
なんで!?

たしかに…
これらの三角形は、平行な線に挟まれていないんだけどね
それぞれの三角形をちょっと詳しく見ていこうか。
△ABOって、△ABCから△OBCを取り除いたものって考えることができるよね。
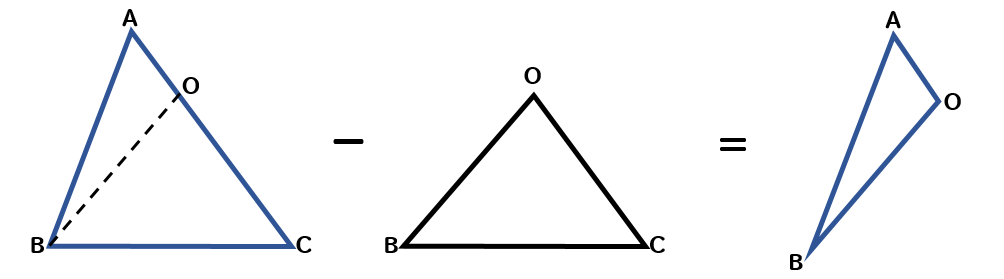
同様に
△DOCも△DBCから△OBCを取り除いたものって考えることができます。
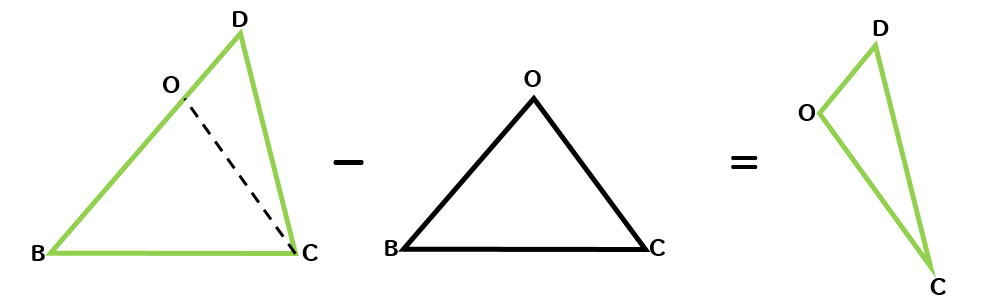
平行線と面積の性質を使って
△ABC=△DBCっていうことがわかっているから
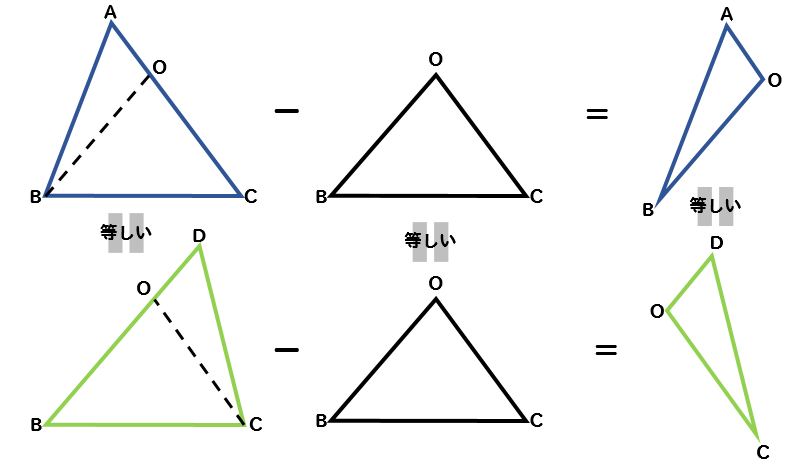
同じ面積の三角形から、同じ三角形(△OBC)を取り除いて
できあがった図形は(△ABOと△DCO)
もちろん面積が等しくなるはずだよね!
だからです。
台形の中から等しい三角形を見つける問題では



このように3組の等しい三角形を見つけることができました。
△ABO=△DCOとなる証明
上で△ABO=△DCOとなる理由をお話しましたが
テストなどでは、これを証明として問われることがあります。
△ABO=△DCOであることを証明しなさい。

平行線と面積の性質より
△ABC=△DCB…①
△ABO=△ABC-△OBC…②
△DCO=△DCB-△OBC…③
①②③より
△ABO=△DCO
上で説明したようなことを
かしこまった数式で表現するとこのようになりますね。

平行四辺形の中から等しい三角形を見つける
下の図で、四角形ABCDは平行四辺形であり、EF//BDである。このとき、△CDFと面積の等しい三角形をすべて答えなさい。
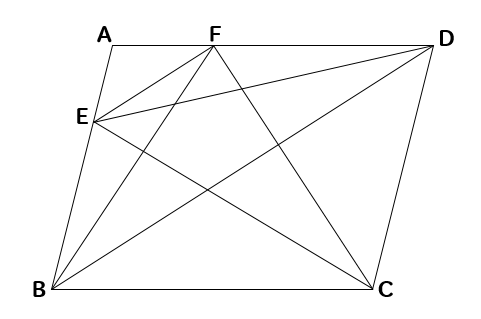
まず、平行四辺形ということから
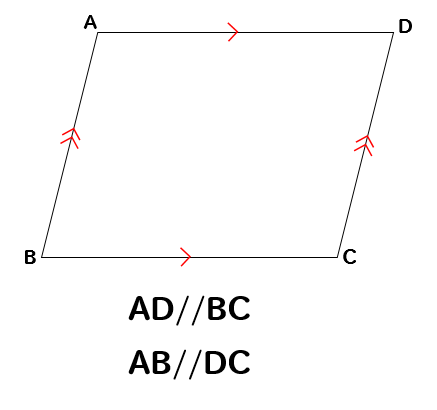
向かい合う辺がそれぞれ平行になっているという点をおさえておこう。
そして、この平行線を利用して考えていくと
底辺をFDとして考えると
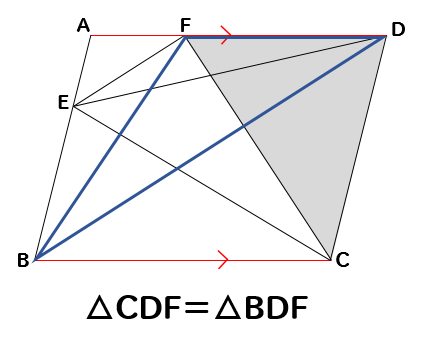
△CDF=△BDFということがわかります。
次に、底辺をBDとして考えると
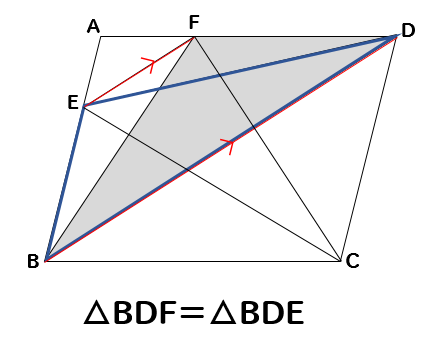
△BDF=△BDEということがわかります。
最後に、底辺をEBとして考えると
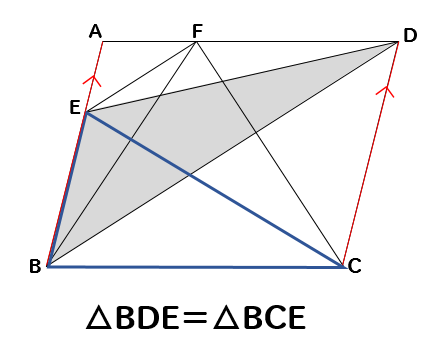
△BDE=△BCEということがわかります。
よって、すべての情報をまとめると
△CDF=△BDF=△BDE=△BCE
となります。
よって、答えは
平行四辺形の中から等しい三角形を見つけていく場合には
リレーをしていくように、面積の等しくなる三角形を見つけていくのがポイントですね。
詳しくはこちらの記事でも解説しています(^^)
平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説!
等積変形の作図問題
等積変形の性質を利用した作図問題を解説していきます。
三角定規を使って平行な線をひく必要がありますので
平行な線のひき方を確認しておきましょう。
平行な線のひき方

三角定規を2つ組み合わせて、線に合わせてセットします。
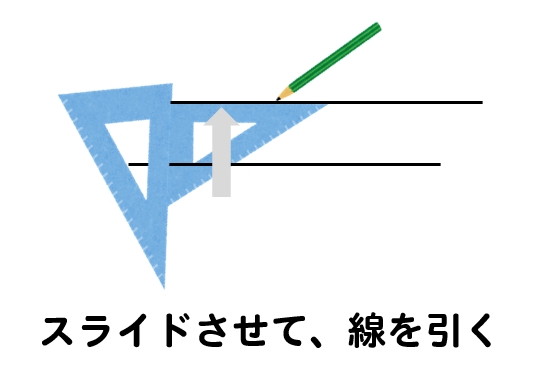
線をひきたいところまで、三角定規をスライドさせて線をひきます。
これで完成です。
では、この作図方法を利用して問題に挑戦していきましょう。
四角形から三角形への等積変形の作図
下の図の四角形ABCDと面積の等しい△ABEを作図しなさい。ただし、点EはBCの右側の延長上にあるようにしなさい。
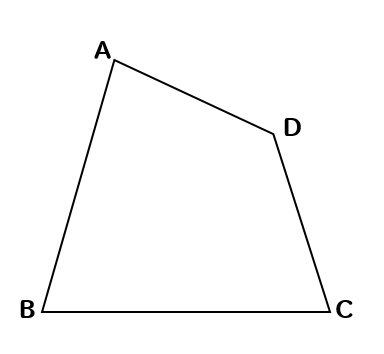
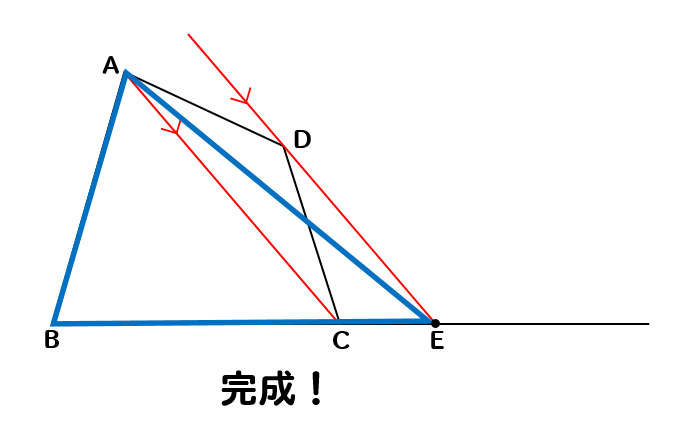
まずは、対角線ACをひきます。
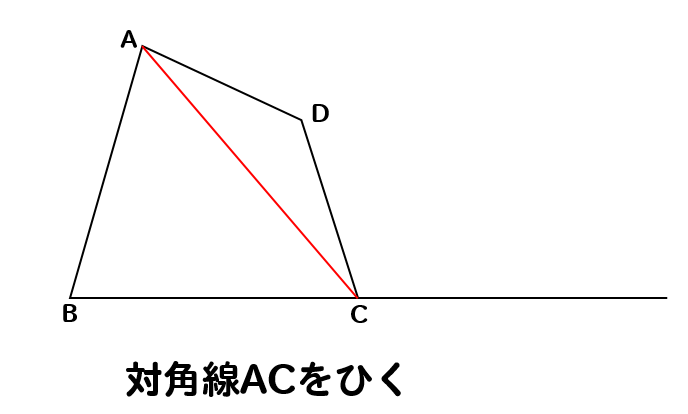
次に辺ACと平行な線を点Dを通るようにひきます。

直線BCとの交点を点Eとすると
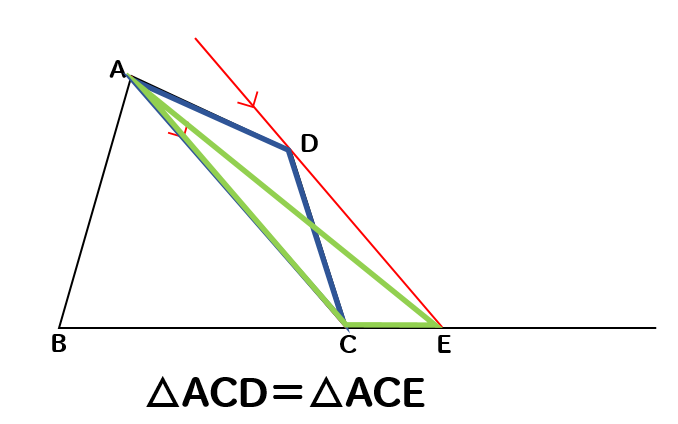
平行線と面積の性質から
△ACD=△ACEとなります。
よって
$${四角形ABCD=△ABC+△ACD}$$
$${=△ABC+△ACE}$$
$${=△ABE}$$
となるので
△ABEは四角形ABCDと面積が等しい三角形だということがわかります。
五角形から三角形への等積変形の作図
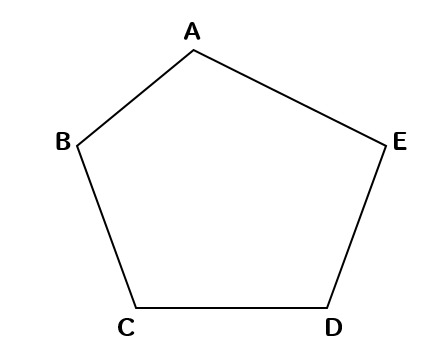
下の図の五角形ABCDEと面積が等しい△AFGをつくりなさい。ただし、点F、Gは直線CD上にあり、点FはCの左側、点GはDの右側にあるようにしなさい。
対角線ACとADをひいて
それぞれに平行な線を点B、Eを通るように線をひきましょう。
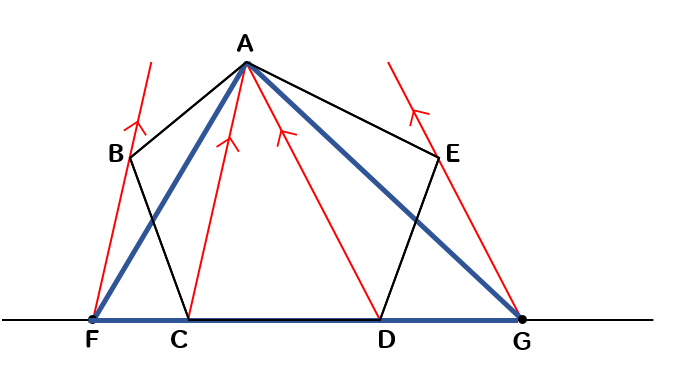
それぞれの線が、直線CDと交わる点を点F、Gとすると
△AFGは五角形ABCDEと面積が等しくなります。
面積は等しいまま境界線をひく作図
下の図のように、長方形が折れ線ABCで2つの部分ア、イに分かれている。点Aを通り、それぞれの部分の面積を変えないように直線AHをひきなさい。ただし、点Hは点Cを通る長方形の辺の上にあるようにしなさい。

まずは直線ACをひきます。
次に、点Bを通るように直線ACと平行な線をひいたら
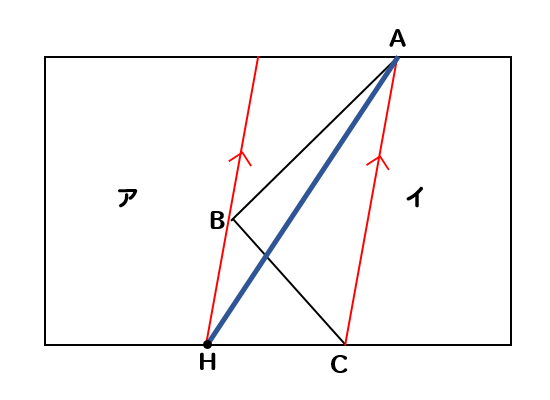
長方形の下の辺と交わった点をHとします。
すると、直線AHはアとイの境界線となります。
イメージとしては
イのはみ出している△ABCを
面積を変えずに下にずらしてやった感じですね。
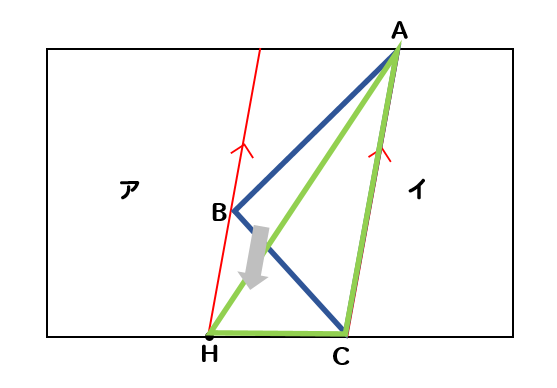
そうすれば、ア・イそれぞれ面積を変えずに
境界線をひき直すことができます。
まとめ
お疲れ様でした!
等積変形についての問題は
等しい三角形を見つける
面積が等しくなるように作図する
この2点をしっかりをおさえておけば大丈夫です!
特に平行四辺形の中から等しい三角形を見つける問題は複雑なので
たくさん練習をして、理解を深めておいてくださいね。
平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説!
ファイトだー(/・ω・)/
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説!
【直角三角形】証明問題の書き方とは?合同条件の使い方を徹底解説!

















わかりやすく
受験に使える!
ようやく理解できた!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!