今回は回転移動の中心を求める作図について考えていこう!
回転移動とは、こんな感じでしたね。
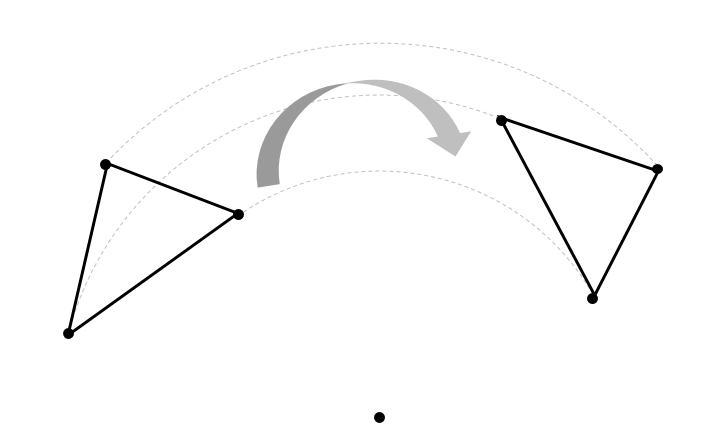
ある点を中心として、図形をぐるっと回転させる移動のこと。
それでは、次のような問題では
次の図形はある点を中心として回転移動したものです。その中心となる点を作図しなさい。
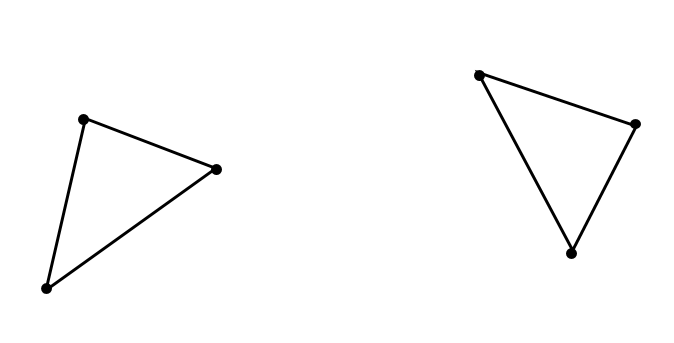
どのように回転移動の中心を求めれば良いのでしょうか?
回転移動の特徴を押さえながら考えていきましょう!
回転移動の特徴を学ぼう!
まずは回転移動の特徴をおさえておきましょう。
中心と対応する点を結ぶと、角度が等しくなる!
回転移動した図形の対応する点と中心を結んだときにできる角度は
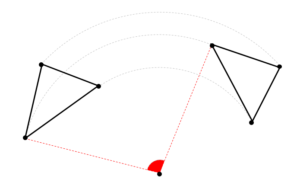
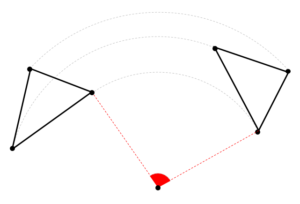
このようにどの点をとってできる角度も等しくなるという特徴があります。
このときにできる角の大きさは、どれくらい回転させたのかを表しています。
中心と対応する点を結んだ線の長さは等しくなる!
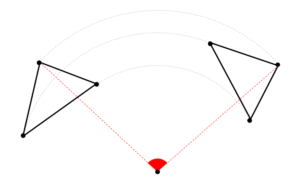
回転移動した図形の対応する点と中心を結んだ線の長さは等しくなります。
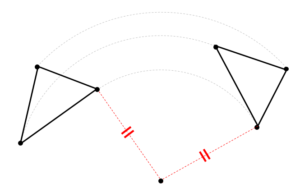
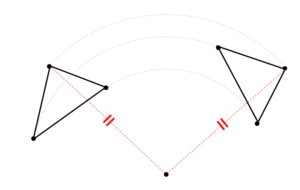
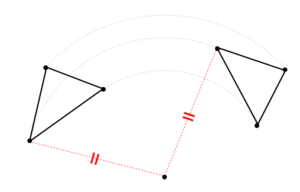
このように対応する点と中心を結ぶと
線分の長さが等しくなるという特徴があるんですね!
つまり
『回転の中心とは、それぞれの対応する点から等しい距離にある』
ということが分かります。
この特徴をおさえておけば…
回転の中心は、それぞれの対応する点の垂直二等分線上にあるということが分かるわけですね!
なぜ垂直二等分線!?
と、思った方はこちらを思い出しておきましょう。
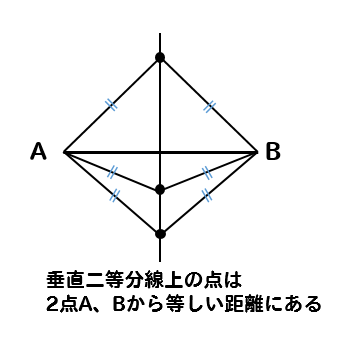
垂直二等分線とは、2点から等しい距離にある点を作図したいときに活用することができましたね!
それでは、これを活用して回転移動の中心を求める作図をやっていきましょう!

回転移動の中心を作図する
上の特徴から、回転移動の中心とは
それぞれの対応する点の垂直二等分線が交わるところ
これが回転移動の中心になるということがわかります。
よって、それぞれの垂直二等分線を作図していきましょう。
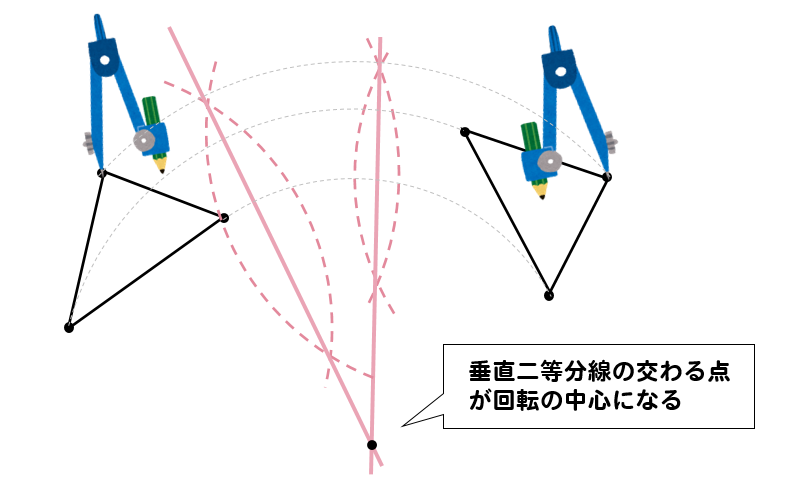
すると、このように垂直二等分線が交わる点が回転移動の中心ということになります!
以上!
回転移動の中心作図まとめ
回転移動した図形は
対応する点と中心を結ぶとそれぞれの線分の長さが等しくなります。
よって、それぞれの対応する点の垂直二等分線を作図し、その交点を求めることで回転移動の中心を作図することができます。
ちょっと覚えておかないと
なかなか思いつくことができない作図ですよね
数学が得意な人でも解けないことが多い問題です。
だから、この記事を通してしっかりと理解しておいてくださいね(/・ω・)/

















わかりやすかったです
ありがとうございます!!
わかりやうい
よかったぁ、嬉しいです^^
わかりやすすぎます
ありがたい
わかりやすいです!
期末テストで出てきたけどわからなかったのですが、このサイトでめちゃくちゃわかりました!語彙力なくてごめんなさいww
理解してもらえたようで嬉しいです^^
苦手な部分だったのでとても助かりましたm(*_ _)m
助かりましたm(*_ _)m