【中１ 作図】円の中心を求める方法を解説！

今回は中1で学習する作図の単元から

円の中心を求める方法について解説していくよ！

円の中心を求める作図とは以下のような問題です。

問題

円の中心Oを作図しなさい。

問題

3点A、B、Cを通るような円Oを作図しなさい。

それでは、円の作図をするために必要な知識と

それぞれの問題の解説をおこなっていきます。

今回の記事は、こちらの動画でも解説しています(/・ω・)/

記事の最後に「理解を定着させる確認シート」「応用を高めるプラス演習」を用意しています。

今回の内容がふむふむ…と理解できた方は、こちらの課題にもチャレンジしてみましょう＾＾

円の中心を作図するために知っておきたいこと

円の中心とは

円周上のどの点からも距離が等しいところにあります。

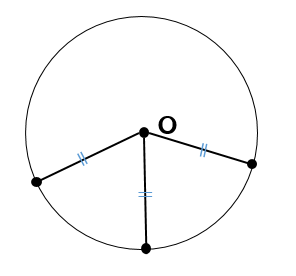
つまり、円の中心を作図したい場合

円周上のどの点からも等しくなるような点を作図することができれば良いということになります。

そこで活躍するのが

垂直二等分線です。

垂直二等分線とは、線分を垂直に二等分するだけでなく

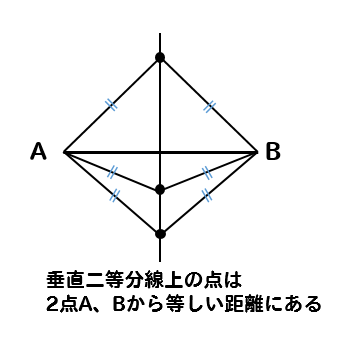
このように、垂直二等分線上に点をとったとき

2点A、Bから等しい距離にあるという特徴があります。

これを利用して円周上から等しい距離にある中心Oを求めていくことになります。

では、忘れてしまった人のために

垂直二等分線の作図方法もまとめておきます。

バッチリ覚えてる！という方は問題の解説に進んでください。

垂直二等分線の作図方法

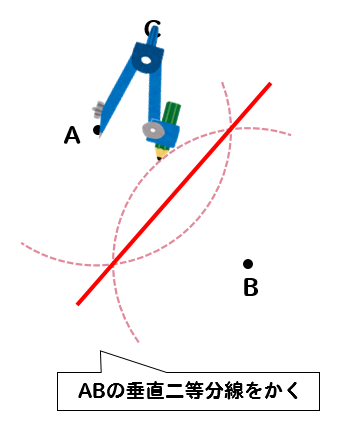
それでは、線分ABの垂直二等分線を作図してみましょう。

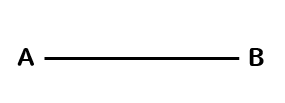
まず、点Aと点Bにコンパスの針を置いて

同じ半径を持つ円をそれぞれかきます。

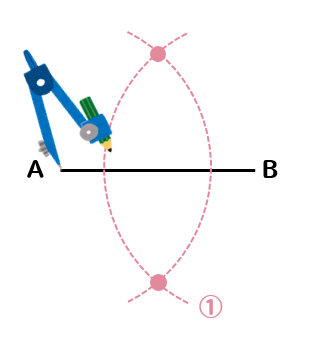
そして、2つの円が交わったところを線で結べば完成です！

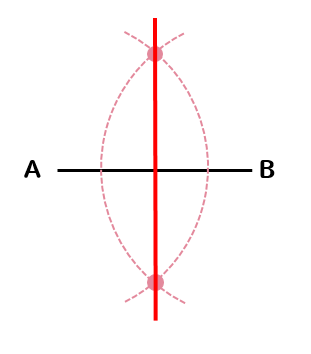
簡単ですね！

覚えておきたいポイント
円の中心は、円周上のどの点からも距離が等しい。垂直二等分線を作図することで2点から等しい距離にある点を作図できる。垂直二等分線の作図方法

1. 2点にコンパスの針を置いて、同じ半径を持つ円をかく
2. 2つの円の交点を線で結ぶ

円の中心を作図する方法

問題

円の中心Oを作図しなさい。

それでは、こちらの作図をやっていきましょう。

垂直二等分線を使って、円周上から等しい距離にある点を見つけていきます。

まずは、自由に円周上に3つ点をとります。

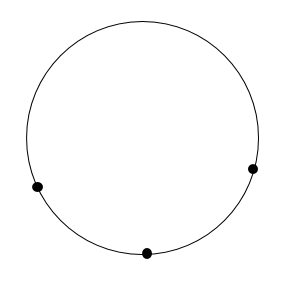
次にそれぞれの点に対して垂直二等分線を作図します。

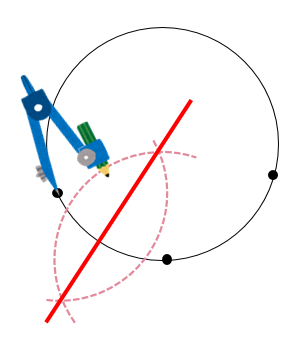
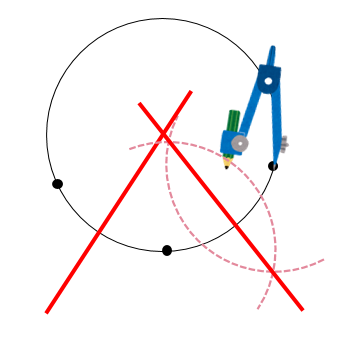
そして、2つの垂直二等分線が交わるところが中心Oとなります。

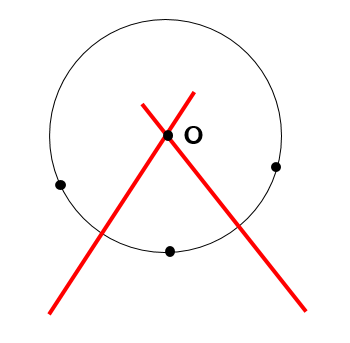
完成！

めっちゃ簡単だね

なんで、これで中心が求まるんだっけ？

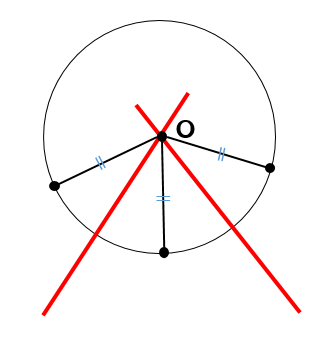
垂直二等分線上の点は、2点からの距離が等しくなるんだったよね。

だから、垂直二等分線どうしが交わる点というのは全ての点から等しい距離にある点だっていうことになります。

3点を通る円を作図する方法

問題

3点A、B、Cを通るような円Oを作図しなさい。

さっきとは少し違う問題ですが、考え方は同じです。

3点を通る円の作図の考え方としては

円の中心を求める⇒中心にコンパスの針を置いて円をかく

という手順になります。

それでは、先ほどの問題と同じように

円の中心を求めていきましょう。

3点のうち2組の垂直二等分線をかきます。

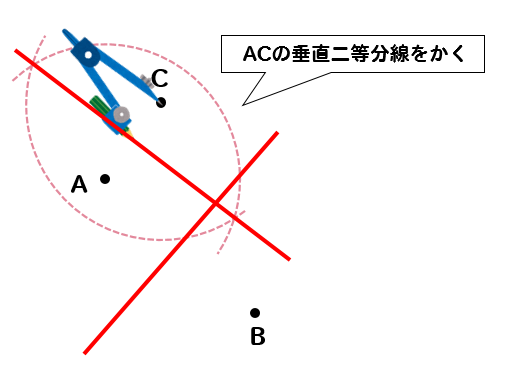
2つの垂直二等分線が交わったところが円の中心となります。

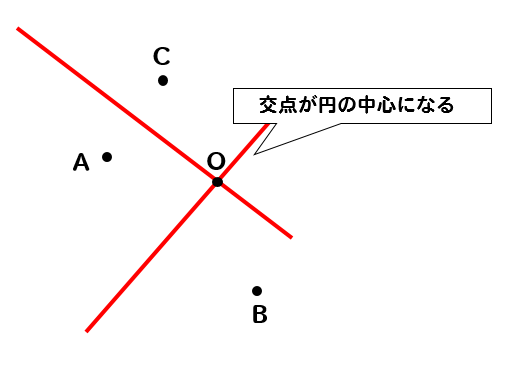
円の中心が作図できたら

中心の点にコンパスの針を置いて

その点からA、B、Cどの点でもいいので

コンパスで長さを取ってやります。

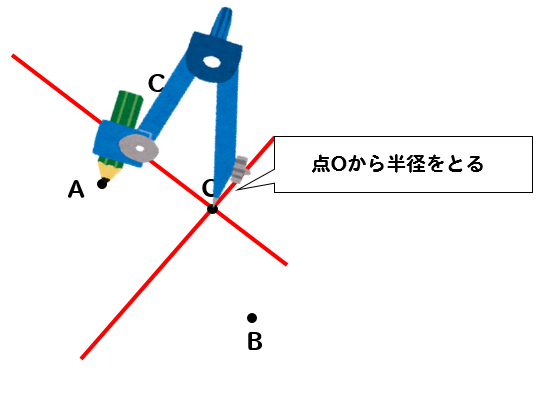
この長さが円の半径となります。

最後に、その長さでコンパスをぐるっと回せば

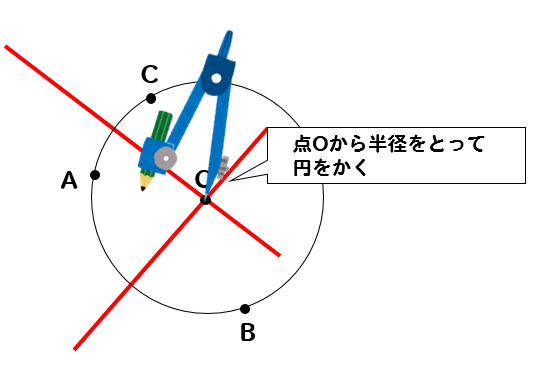
3点を通る円の完成です！

テストで解ける！確認シート＆応用高めるプラス演習

今回の内容をしっかりと定着させ、テストで確実に得点できるようにするため、円の中心作図に関する「確認シート」「応用を高めるプラス演習」を用意しました。

もしも親御さんがこの記事を読んでくださってる場合は、こちらの確認課題を使ってお子さんと一緒に作図演習に取り組んでみてください。

そうすればわざわざこの記事をお子さんに見せなくても、プリントを活用しながら学ぶことができますよ＾＾

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます。

手を動かして作図を体験することで「テストでできる！」を実感することができますよ＾＾

こちらから今すぐチャレンジしてみよう！

円の中心の作図方法　まとめ

お疲れ様でした！

円の中心の作図は全然難しいものではありませんでしたね。

中心は、円周上のどの点からも等しい距離にある。

垂直二等分線を利用すると、2点から等しい距離にある点が作図できる。

この2点をしっかりと理解できていれば大丈夫です。

たくさん練習して、必ず解けるようにしておこう！

定期テストでも必須の問題だからね！

ファイトだー(/・ω・)/