今回は中１で学習する作図の単元から
3辺から等しい距離にある点の作図問題に挑戦していきましょう！
問題
下の図の△ABCの3辺から等しい距離にある点Pを作図しなさい。
Contents
角の二等分線の作図方法と特徴
今回の問題を解くためには
角の二等分線の作図について詳しく理解しておく必要があります。
まず、角の二等分線にはどのような特徴があるか確認しておきましょう。
角の二等分線の特徴
角の二等分線とは、名前の通り角を二等分にする線のことですね。
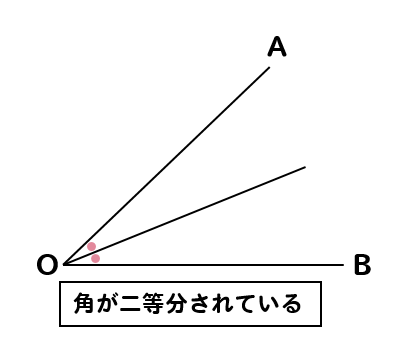
60°の角に二等分線を作図すると
角は30°と30°に分けることができます。
このことは多くの人が理解していますが
角の二等分線には、他にもこんな特徴があるのをご存知でしょうか？
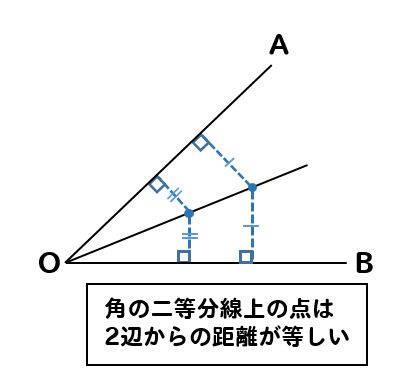
角の二等分線上の点は、2辺OAとOBからの距離が等しくなる。
という特徴もあります。
つまり
角の二等分線は、角を半分にするということだけでなく
2辺からの距離が等しくなる点を集めて線にしたもの。
と、考えることができるのです。
よって
2辺からの距離が等しくなるような作図をしたいときには
角の二等分線が活躍することになります。
角の二等分線の作図方法
それでは、角の二等分線とは
どのように作図すればよいのか説明していきます。
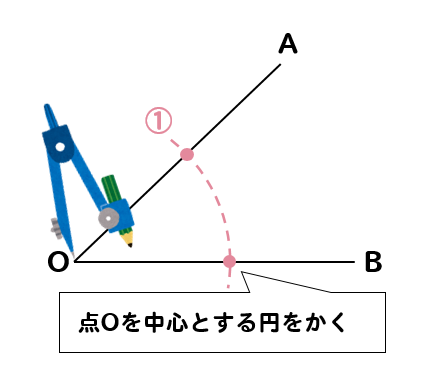
まずは、二等分したい角の上にコンパスの針を置いて
点Oを中心とする円をかきます。
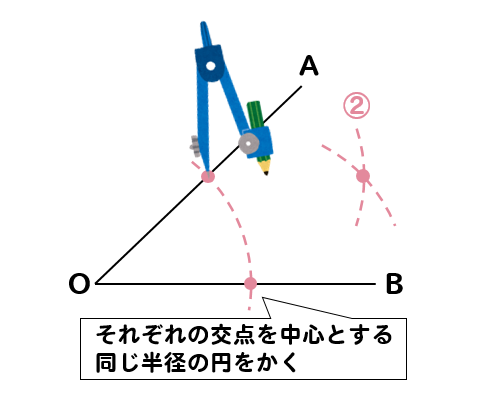
先ほどかいた円とOA、OBとの交点にコンパスの針を置いて
それぞれを中心とする同じ半径の円を２つかきます。
最後に、先ほどかいた２つの円の交点と点Oを線で結べば完成です！
角の二等分線の作図方法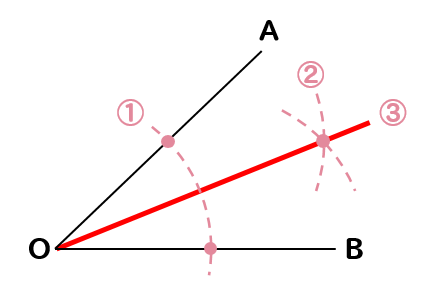
- 点Oを中心とする円をかく。
- OA、OBとの交点を中心とする同じ半径の円をかく。
- ２つの円の交点と点Oを線で結ぶ。完成！
問題の答え＆解説
それでは、今回の問題を考えてみましょう。
問題の答え
まずは、∠Bを二等分する線をかきます。
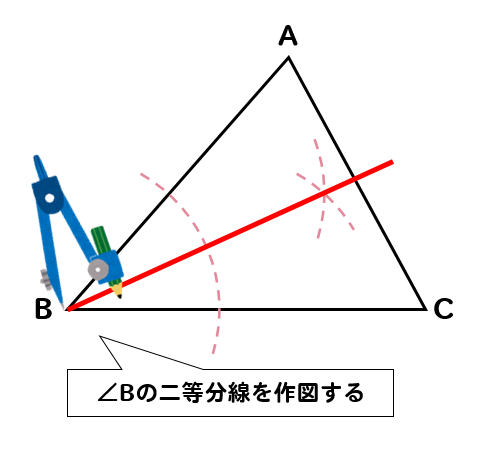
次に、∠Cを二等分する線をかきます。
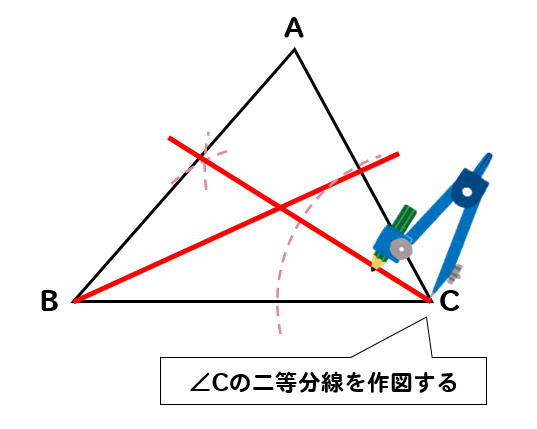
２つの二等分線が交わるところが点Pとなります。完成！
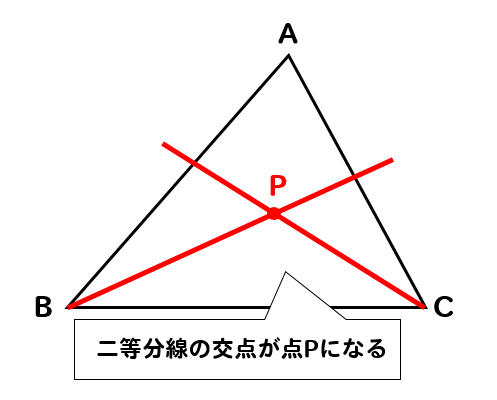
問題の解説
なぜこのような手順で、3辺から等しい距離にある点を作図できるのか説明していきます。
まず、∠Bの二等分線をかくことで
辺BA、BCから等しい距離にある点が集まる線をかくことができます。
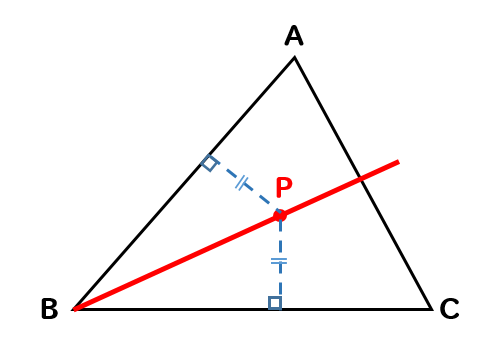
同様に∠Cの二等分線をかくことで
辺CB、CAから等しい距離にある点が集まる線をかくことができます。
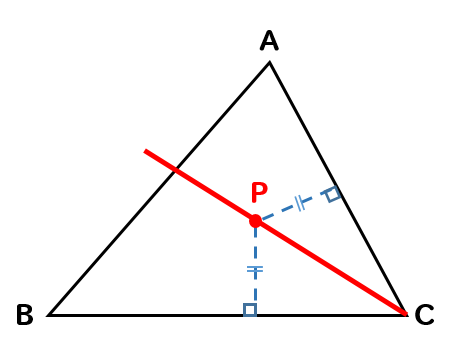
よって、この２つを組み合わせて考えてみると
それぞれの二等分線の交点は
辺AB、BC、CAからそれぞれ等しい距離にある点だということになります。
3辺から等しい距離にある点の作図 まとめ
お疲れ様でした！
3辺から等しい距離にある点ってなに！？
そんな作図習ってないよ！！
って思っちゃいますが
角の二等分線を利用することで作図することができます。
いろんな問題がありますが
『〇辺から等しい距離にある点』というワードが問題文にあれば
角の二等分線を利用して考えてみましょう！
角の二等分線は
2辺からの距離が等しい点を集めた線のこと！
しっかり覚えておきましょう。
ファイトだー(/・ω・)/
効率よく学習を進めていきたい方は必見！
この記事を通して、学習していただいた方の中にはもっといろんな単元の学習を進めていきたい！
という素晴らしい学習意欲を持っておられる方もいる事でしょう。
だけど
どこの単元を学習すればよいのだろうか。
何を使って学習すればよいのだろうか。
勉強を頑張りたいけど 何をしたらよいか悩んでしまって
手が止まってしまう…
そんなお悩みをお持ちの方もおられるのではないでしょうか。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで
どの単元を学習すればよいのか 何を解けばよいのか
そういった悩みを全て解決することができます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
- 費用が安い！月額1980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
今までの悩みを解決し、効率よく学習を進めていきましょう。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
数スタの公式LINEを開設しました！