今回は、「平行な2直線の距離」を求める問題について解説していきます。
直線と直線の距離とは、次のような問題ですね。
【問題】
2直線 \(5x+4y=10\)、\(5x+4y=30\)の間の距離を求めなさい。
この問題を解くためには、点と直線の距離を求める公式を使いこなせる必要があります。
ちょっと不安だ…という方は
>【点と直線の距離】公式の覚え方と使い方をイチから解説するぞ!
こちらの記事で確認しておいてください。
今回の内容をサクッと理解した方は、こちらの動画をどうぞ!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
【直線と直線の距離】平行な2直線の距離を求める方法を解説!
それでは、問題を解いてみましょう。
【問題】
2直線 \(5x+4y=10\)、\(5x+4y=30\)の間の距離を求めなさい。
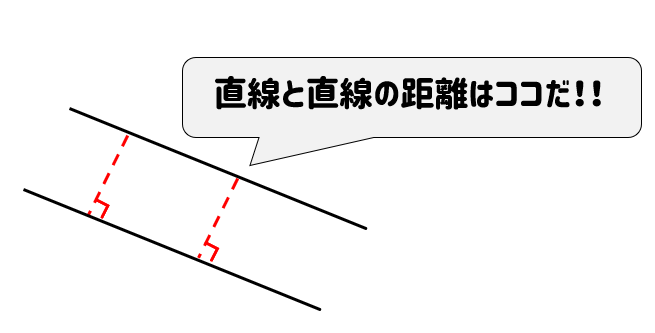
手順はとってもシンプルです。
平行な2直線の距離を求める手順!
- 直線上の点の座標を求める
- ①の点ともう一方の直線の距離を求める
- 完成!
それでは、手順に従ってやっていきましょう。
まずは、直線上の点の座標を求めます。
\(5x+4y=10\) の式に \(y=0\) を代入すると
$$\begin{eqnarray}5x&=&10\\[5pt]x&=&2 \end{eqnarray}$$
つまり、\(5x+4y=10\) の直線上に\((2,0)\) という点があるということが分かります。
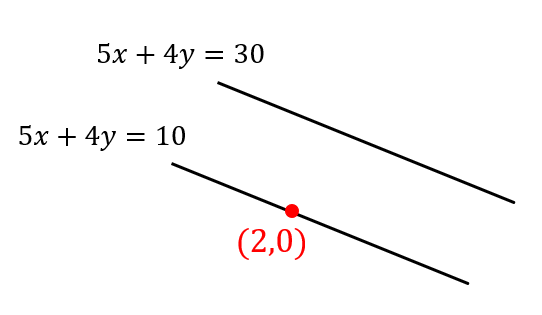
直線上の点の座標を求めるとき
今後の計算をなるべくラクにしたいので、\(x=0\) もしくは\(y=0\) を代入してシンプルな値の座標を求めましょう。
次に、\((2,0)\) ともう一方の直線\(5x+4y=30\) の距離を求めましょう。
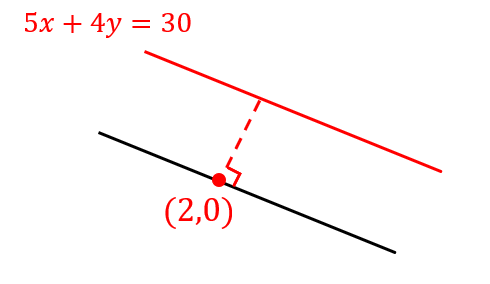
点と直線の距離を求める公式点\((x_1,y_1)\)と直線\(ax+by+c=0\)の距離
$$\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
$$\begin{eqnarray}\frac{|10+0-30|}{\sqrt{5^2+4^2}}&=&\frac{20}{\sqrt{41}} \\[5pt]&=&\frac{20\sqrt{41}}{\sqrt{41}}\end{eqnarray}$$
これで完成!
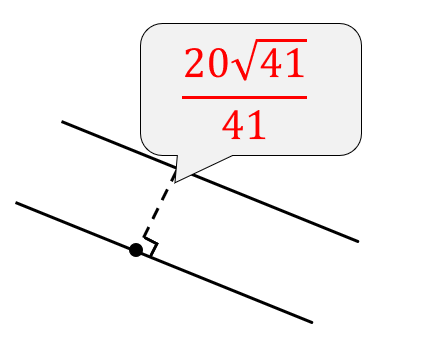
平行な2直線の距離を求める公式はありません。
なので、点と直線の距離の公式を用いて求めていきます。
点と直線の公式に当てはめるためには、点の座標が必要ですね。
というわけで、まずは点の座標を求める!というわけです。
考え方と手順を知ってしまえば、とっても簡単な問題でしたね(^^)
【直線と直線の距離】平行な2直線の距離の求め方まとめ!
お疲れ様でした!
最後に手順を確認しておきましょう。
平行な2直線の距離を求める手順!
- 直線上の点の座標を求める
- ①の点ともう一方の直線の距離を求める
- 完成!
今回の問題は意味が分かれば簡単なものです。
サクッと得点しちゃいましょう(/・ω・)/

















コメントを残す