【数学Ⅰ】f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう！

高校数学Ⅰで学習する2次関数の単元から

「$f(x)>g(x)$ の範囲の求め方」

について解説していきます。

 

この問題では、

「すべての実数 $x$ について」

「ある実数 $x$ について」

「すべての実数 $x_{1},x_{2}$ に対して」

「ある実数 $x_{1},x_{2}$ に対して」

といった表現が出てきます。

これらの違いについて理解した上で、どのように問題を解いていけばよいのか考えていきましょう。

 

今回取り上げる問題はこちらです。

 

今回の内容をサクッと理解したい方は、こちらの動画がおススメです！

問題（1）すべての実数$x$ に対して

すべての実数 $x$ に対して $f(x)>g(x)$ が成立するというのは、

区間の中において、同じ $x$ 座標のところを比べると $f(x)$ の方が $g(x)$ よりも上にあるということを意味します。

 

なので、ここでは $f(x)-g(x)$ の関数を考え、

この関数の区間内においての最小値が正であれば、

$f(x)$ が常に上にあるということが言えます。

 

したがって、

$$\begin{eqnarray}&&f(x)-g(x)\\[5pt]&=&(x-1)^2 -(-2x^2-4x+a)\\[5pt]&=&x^2-2x+1+2x^2+4x-a\\[5pt]&=&3x^2+2x+1-a\\[5pt]&=&3\left(x^2+\frac{2}{3}x\right)+1-a\\[5pt]&=&3\left(x+\frac{1}{3}\right)^2+\frac{2}{3}-a\end{eqnarray}$$

$-2≦x≦2$ の区間において、最小値は $\frac{2}{3}-a$ となる。

よって、

$$\begin{eqnarray}\frac{2}{3}-a&>&0 \\[5pt]a&<&\frac{2}{3}\cdots(解)\end{eqnarray}$$

 

問題（2）ある実数 $x$ に対して

ある実数 $x$ に対して $f(x)>g(x)$ が成立するというのは、

区間の中において、同じ $x$ 座標のところを比べたとき、1ヵ所でもいいから、$f(x)$ が $g(x)$ よりも大きくなっているところがあるということを表しています。

このような違いになっています。

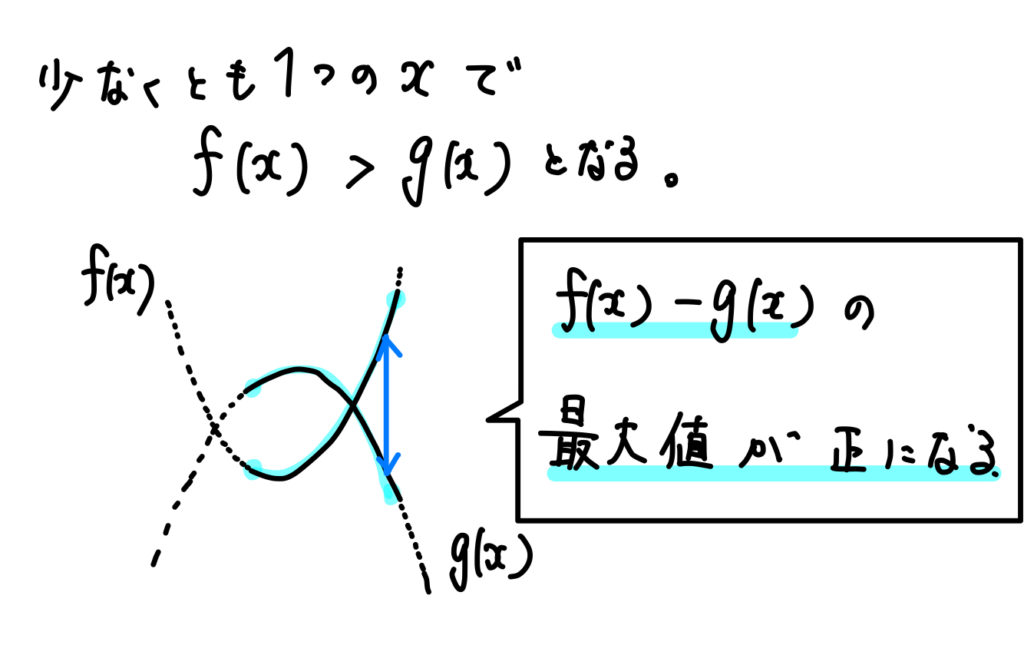
なので、ここでも $f(x)-g(x)$ の関数を考え、

この関数の区間内においての最大値が正であれば、

$f(x)$ が $g(x)$ よりも上になっている部分があるということが言えます。

 

したがって、

$$\begin{eqnarray}&&f(x)-g(x)&=&3\left(x+\frac{1}{3}\right)^2+\frac{2}{3}-a\end{eqnarray}$$

$-2≦x≦2$ の区間において、最大値は $x=2$ のとき、$17-a$ となる。

よって、

$$\begin{eqnarray}17-a&>&0 \\[5pt]a&<&17\cdots(解)\end{eqnarray}$$

 

問題（3）すべての実数 $x_{1},x_{2}$ に対して

すべての実数 $x_{1},x_{2}$ に対して $f(x_{1})>g(x_{2})$ が成立するというのは、

区間内のあらゆる座標を比べたとき、どこを比べたとしても$f(x)$ が $g(x)$ よりも上側にあるということを表しています。

（1）の問題では同じ $x$ 座標のときで比べていましたが、

今回の問題では、同じ $x$ 座標であるという縛りはありません。

 

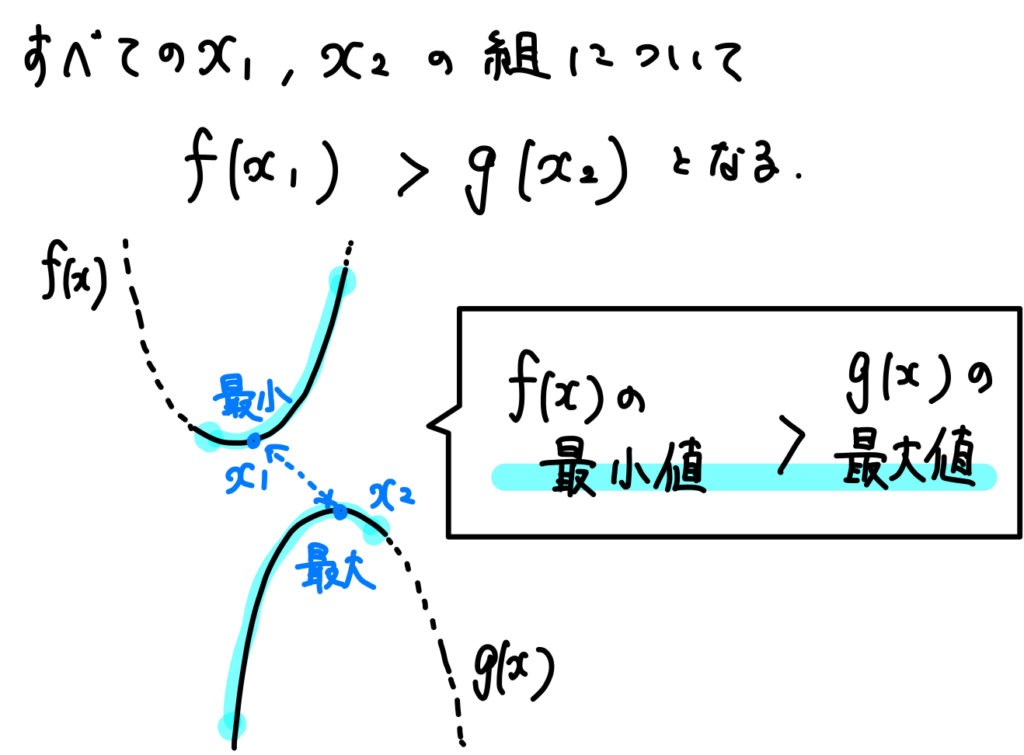
となると、$f(x)$ の最小値が $g(x)$ の最大値よりも大きいならば、区間内のどこを比べても $f(x)$ の方が上にあることになります。

 

というわけで、$f(x)$ の最小値、$g(x)$ の最大値をそれぞれ求めましょう。

$f(x)=(x-1)^2$ であるから、$x=1$ のとき最小値 $0$

$g(x)=-2x^2-4x+a=-2(x+1)^2+2+a$ であるから、$x=-1$ のとき最大値 $2+a$

 

したがって、

$$\begin{eqnarray}0&>&2+a\\[5pt]a&<&-2\cdots(解) \end{eqnarray}$$

 

問題（4）ある実数 $x_{1},x_{2}$ に対して

ある実数 $x_{1},x_{2}$ に対して $f(x_{1})>g(x_{2})$ が成立するというのは、

区間内のどこの座標を比べてもいいので、どこか1ヵ所でいいから $f(x)$ の方が $g(x)$ よりも上側になっていることを表しています。

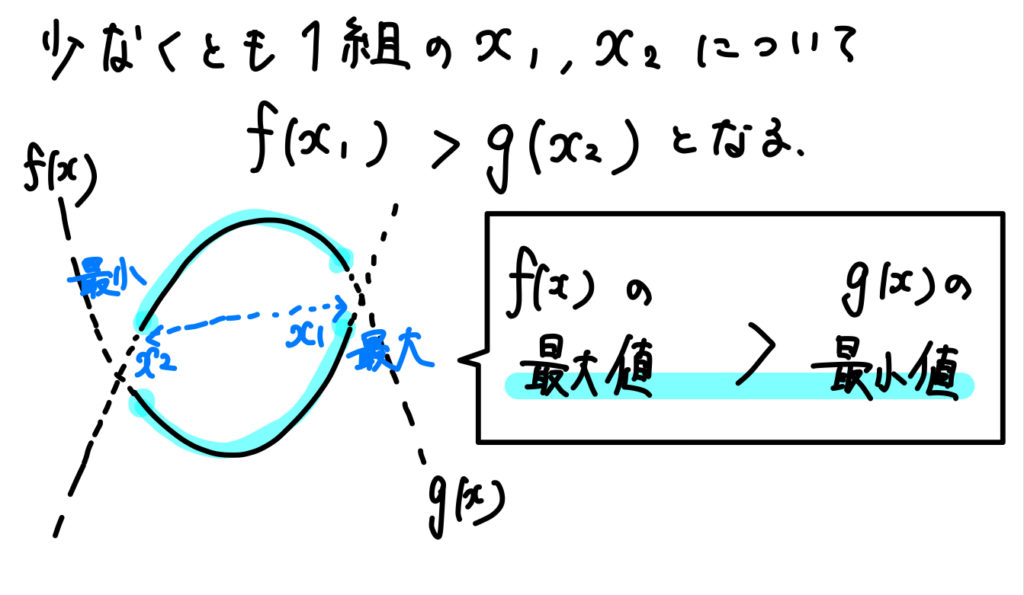
これはちょっとイメージしずらいかもしれませんが(^^;)

上の画像のように、$f(x)$ の最大値が $g(x)$ の最小値よりも大きいならば、$f(x)$ が上側になっている部分があるってことが言えます。

 

というわけで、$f(x)$ の最大値、$g(x)$ の最小値をそれぞれ求めましょう。

$f(x)=(x-1)^2$ であるから、$x=-2$ のとき最大値 $9$

$g(x)=-2x^2-4x+a=-2(x+1)^2+2+a$ であるから、$x=2$ のとき最小値 $-16+a$

 

したがって、

$$\begin{eqnarray}9&>&-16+a\\[5pt]a&<&25\cdots(解) \end{eqnarray}$$

 

まとめ！

お疲れ様でした！

最後にそれぞれの違いと考え方についてまとめておきましょう。