今回の記事では「二次関数の最大・最小の求め方」をイチから解説してきます。
特に、数学が苦手な人に向けて丁寧に解説していくので最後までがんばっていきましょう(^^)
場合分けが必要になる応用問題については別記事で解説をつけていきます。
>【二次関数の場合分け】最大最小の応用問題の解き方をイチから解説!
今回の記事は、動画による解説もつけてます(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
二次関数の最大・最小の求め方(定義域なし)
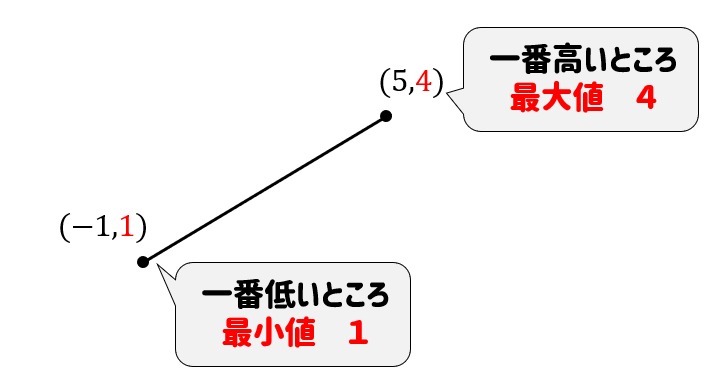
そもそも最大・最小ってなんのこと?って話だね。
これはすっごく簡単なこと!
グラフの中で\(y\)座標が一番大きくなっているところを最大値。
反対に\(y\)座標が一番小さくなっているとっころを最小値といいます。
\(y\)座標…!?
何だかピンと来ないぞ…という方は
グラフが一番高くなっているところが最大値。
グラフが一番低くなっているところが最小値。
という認識でもOKです。
では、二次関数の最大・最小を求める問題を見てみましょう。
【問題】
次の関数の最大値・最小値があればそれぞれ求めよ。また、そのときの\(x\)の値を求めよ。
$$y=x^2-2x+3$$
二次関数の式を見ただけでは、どこが最大で最小なのか判断がつきませんね(^^;)
なので、まずはグラフを書いて見た目で判断ができる状態にしましょう。
二次関数のグラフの書き方については
>【数学苦手な高校生向け】二次関数グラフの書き方を初めから解説!
こちらの記事でイチから解説しているので不安な方はご参考ください。
まずは、グラフを書くためには頂点が必要!
式を平方完成して頂点の座標を求めましょう。
$$\begin{eqnarray}y&=&x^2-2x+3\\[5pt]&=&(x-1)^2-1+3\\[5pt]&=&(x-1)^2+2 \end{eqnarray}$$
以上より、頂点の座標は\((1,2)\) ということが分かりましたね。
次に二次関数の式から、\(x^2\)の前についている数が+なのでグラフの形は下に凸。
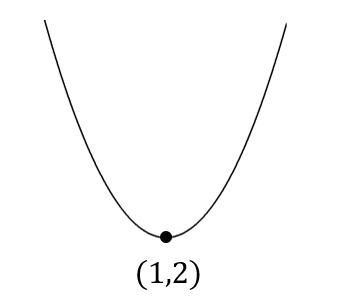
こんな感じになることが分かりますね。
最大値、最小値を求めるためにグラフを書く場合
どこが大きくて小さいかが読み取れればOKなので、わざわざ\(x\)軸、\(y\)軸を書く必要はありません。
形と頂点の座標が分かる程度のシンプルなものでOKです。
グラフが書けたら、どこが最大、最小になるのかを見つけていきましょう。
すると今回のグラフでは…
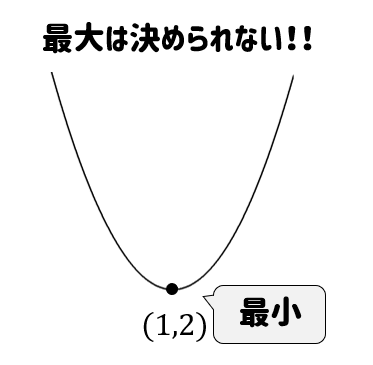
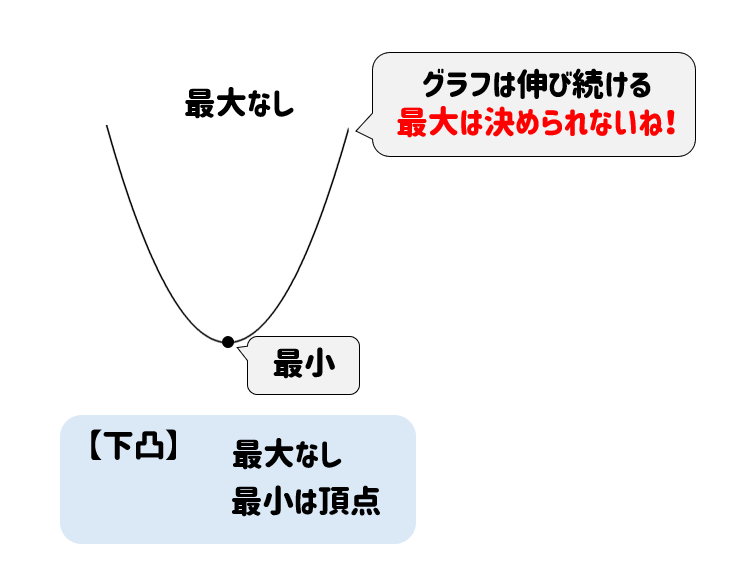
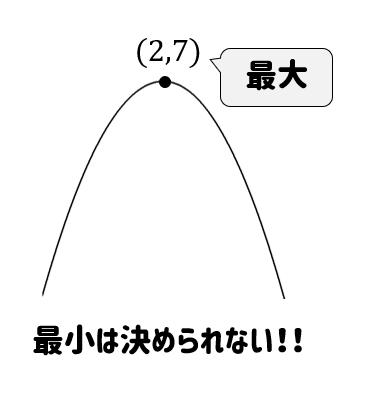
頂点が最小になり、最大は決められない!
ということになります。
最大が決められないってどういうこと!?
って感じだね(^^;)
放物線のグラフっていうのは、書ききれないから省略しているけど
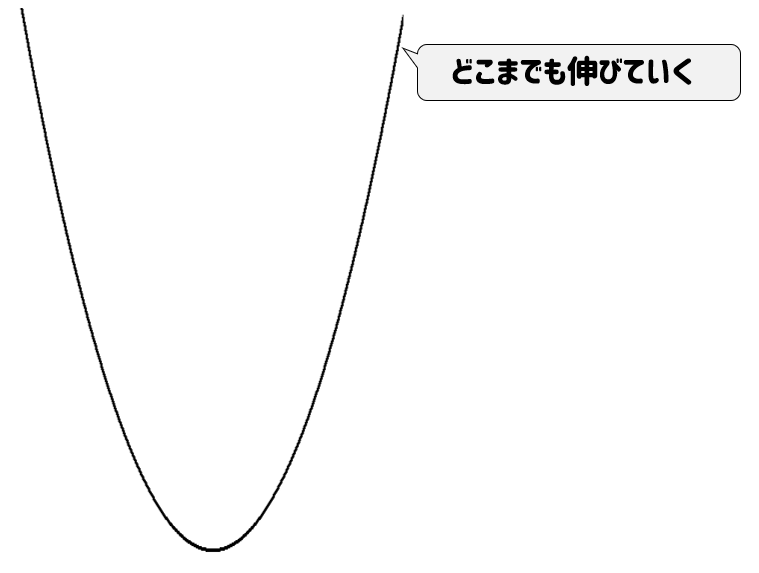
無限に伸びているんだーーーーー!!
だから、一番大きいところっていうのは決められない。
だって、伸び続けているから!
というわけで、今回の問題では最大値はなしってことになります。
ちなみに最小値はパッと見て、頂点の場所だとすぐに判断することができるね。
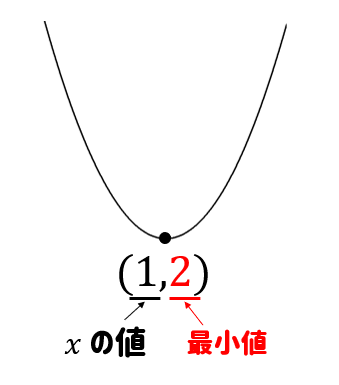
答え
最大値 なし
\(x=1\) のとき 最小値 \(2\)
それでは今の手順にそって、もう1問やってみましょう。
【問題】
次の関数の最大値・最小値があればそれぞれ求めよ。また、そのときの\(x\)の値を求めよ。
$$y=-2x^2+4x+1$$
まずは、頂点の座標を求めてシンプルなグラフを書いていきましょう。
$$\begin{eqnarray}y&=&-2x^2+4x+1\\[5pt]&=&-2(x^2-2x)+1\\[5pt]&=&-2\{(x-1)^2-1\}+1\\[5pt]&=&-2(x-1)^2+2+1\\[5pt]&=&-2(x-1)^2+3 \end{eqnarray}$$
よって、頂点の座標は\((1,3)\)と分かります。
さらに\(x^2\)の前についている数がマイナスであることから上に凸のグラフになりますね。
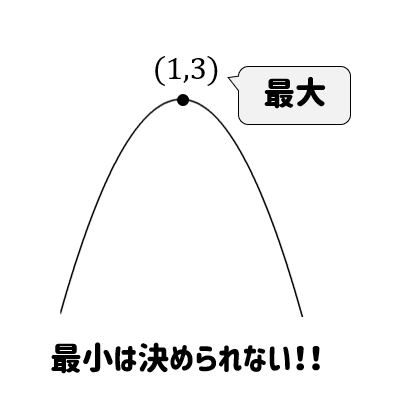
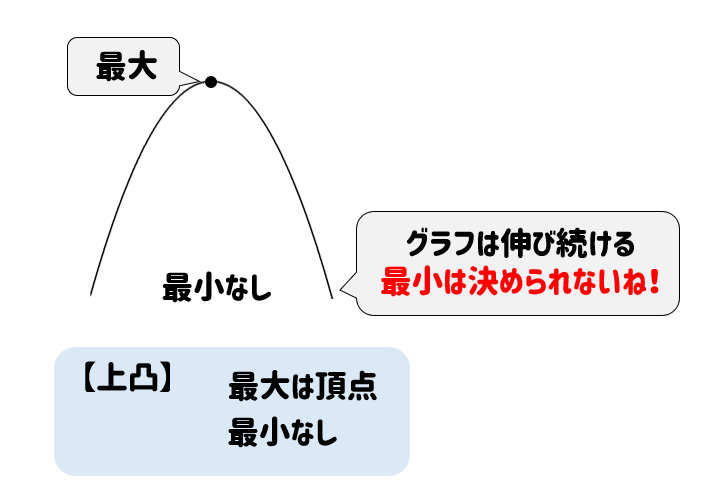
すると今度は、頂点の場所が最大となり、最小は決められない!ということが分かります。
答え
\(x=1\) のとき 最大値 \(3\)
最小値 なし
以上のことから、次のようなことがわかります。
練習問題に挑戦!
【問題】
次の関数の最大値・最小値があればそれぞれ求めよ。また、そのときの\(x\)の値を求めよ。
$$y=x^2+6x-2$$
【問題】
次の関数の最大値・最小値があればそれぞれ求めよ。また、そのときの\(x\)の値を求めよ。
$$y=-x^2+4x+3$$
二次関数の最大・最小の求め方(定義域あり)
【問題】
次の関数に最大値、最小値があればそれぞれ求めよ。また、そのときの \(x\)の値を求めよ。
$$y=x^2-2x+3 (-1≦x≦2)$$
おっと…

式の後ろになにかついていますね。
これは定義域といって、このグラフにおける\(x\)の範囲を表しています。
っていうと難しく感じてしまうので次のように考えてください。
定義域で指定された範囲をカットする!!
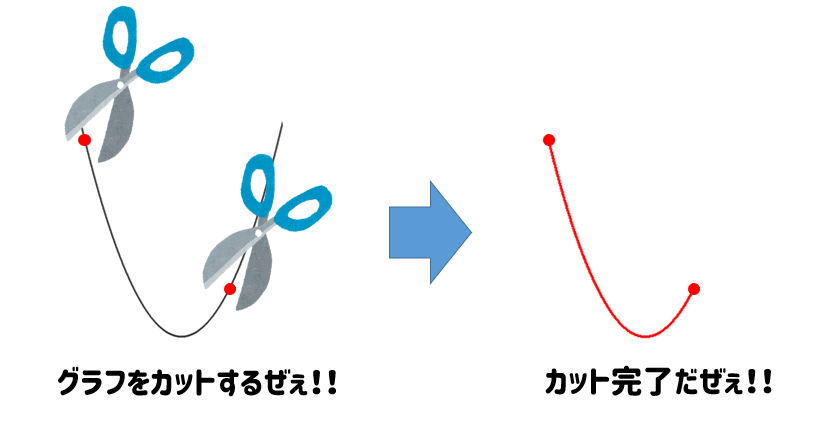
このように、定義域が指定された場合
グラフをカットして考えていくということになります。
グラフをカットするということを頭に入れておいて、先ほどの問題を考えていましょう。
まずは、平方完成して頂点の座標を求める。
$$\begin{eqnarray}y&=&x^2-2x+3\\[5pt]&=&(x-1)^2-1+3\\[5pt]&=&(x-1)^2+2 \end{eqnarray}$$
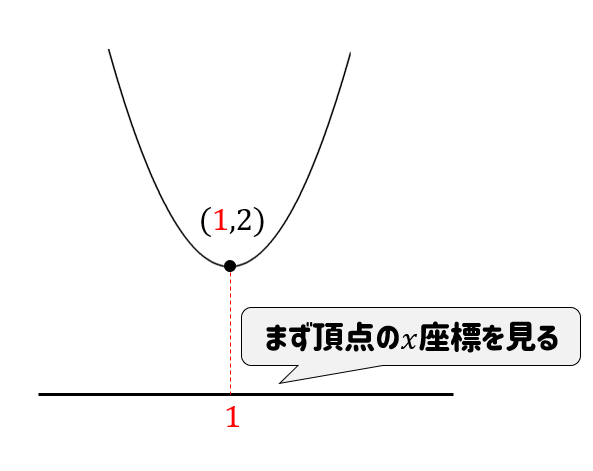
よって、頂点の座標は\((1,2)\) となります。
以上からグラフは次のようになります。

次に、このグラフを定義域で指定された\((-1≦x≦2)\) でカットしていきます。
でも、どこをどのようにカットすれば…?と迷ってしまいそうですが
\(x\)の範囲とはヨコの範囲のことです。
このことを踏まえて次の図のように考えるとカットがしやすくなります。
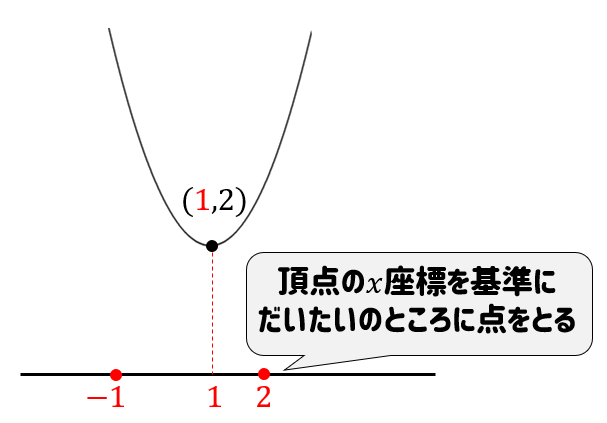
頂点の\(x\)座標を基準にして値を考えていけば、ちゃんとカットすることができます(^^)
上では丁寧に手順を紹介しましたが、慣れてくれば頭の中でパパっとグラフを切り取ることができるようになります。
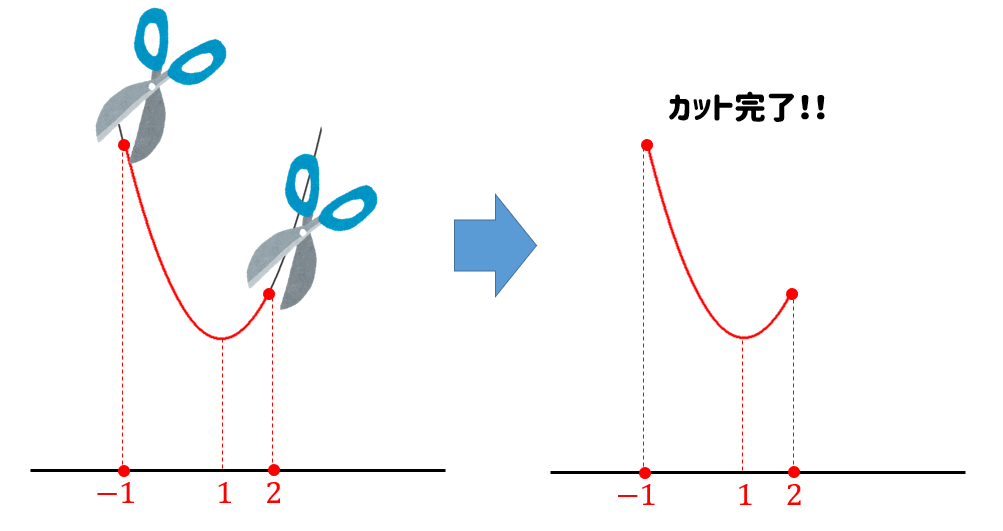
それでは、定義域によってカットされたグラフを見てみましょう。
このカットされたグラフにおいて最大、最小は
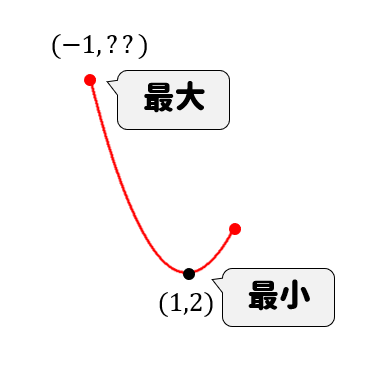
このように見つけることができます。
\(x=-1\) のときの\(y\)座標は二次関数の式に代入すれば求まります。
$$\begin{eqnarray}y=(-1)^2-2(-1)+3=1+2+3=6 \end{eqnarray}$$
よって、\(x=-1\) のとき最大値\(6\)、\(x=1\) のとき最小値\(2\)となります。
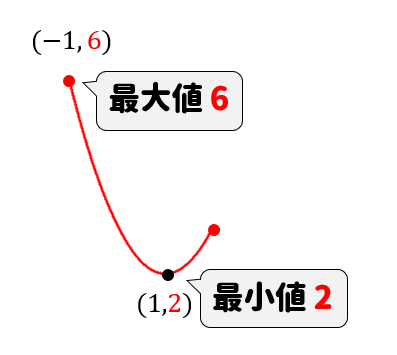
答え
\(x=-1\) のとき最大値\(6\)
\(x=1\) のとき最小値\(2\)
初めはグラフをカットするという作業がちょっとだけ難しいかもしれません。
だけど、やっていることは至ってシンプルです。
グラフを書いて、横の範囲をカットする。
カットされたグラフの中から一番大きいところ、小さいところを見つけるだけ。
これだけのことですね!
ただし!
定義域に関する問題で気を付けたいことがあります。
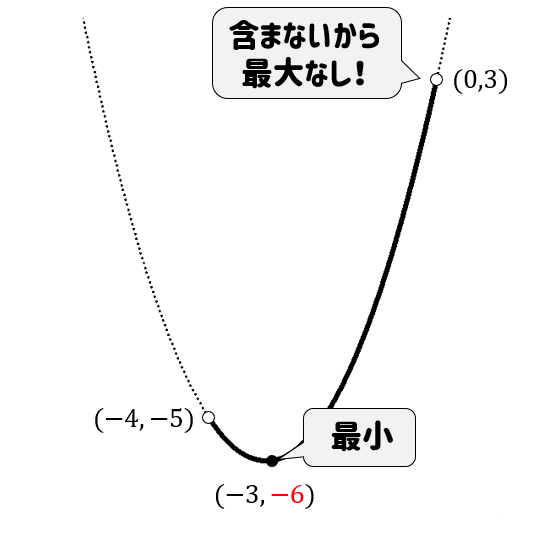
それは定義域の不等号が\((-1<x≦2)\) というようにイコールがついていない<になっているとき。
これはその値を含みませんという意味です。
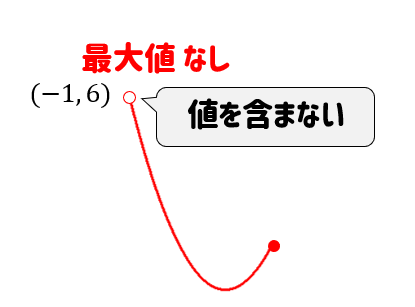
なので、グラフをカットしたとき
最大や最小になるであろう場所が値を含まないになっていると
最大、最小が決められない…ってことになっちゃいます。
というわけで、この場合には最大値なし、最小値なしといった対応をしなければなりませんので定義域の不等号には気を付けてください!
それでは、練習問題を通して理解を深めていきましょう。
練習問題に挑戦!
【問題】
次の関数に最大値、最小値があればそれぞれ求めよ。また、そのときの \(x\)の値を求めよ。
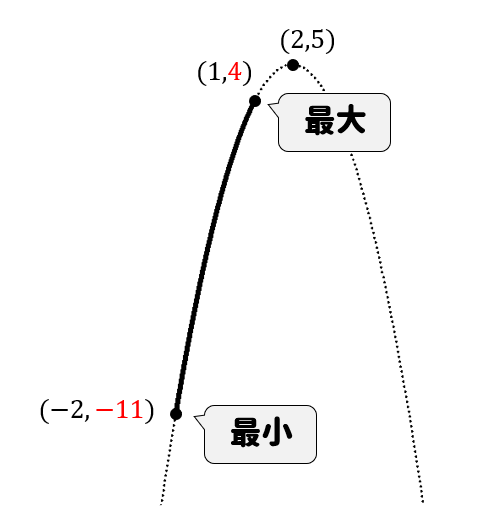
$$y=-x^2+4x+1 (-2≦x≦1)$$
【問題】
次の関数に最大値、最小値があればそれぞれ求めよ。また、そのときの \(x\)の値を求めよ。
$$y=x^2+6x+3 (-4<x<0)$$
まとめ!
お疲れ様でした!
二次関数の最大・最小の問題はいかがでしたでしょうか??
平方完成ができて、簡単なグラフを書けること。
頂点の\(x\)座標を基準にグラフをカットできること。
この2点が揃っていれば、簡単に解くことができますね(^^)
最大・最小の問題は苦手な人が多い単元です。
だからこそ!
この問題を解けるようになっておけば、まわりと差がつけれるってもんだぜ。
ファイトだ(/・ω・)/
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます! ←今回の記事
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!



















凄くわかりやすい解説ありがとうございます!
一つだけ質問があるのですが、最後の練習問題で頂点の座標が(-3,-6)となっているのですが、なぜx座標の「3」にマイナスの符号がつくのでしょうか?
お手すきのときにご返信お願いいたします♂️
とってもていねいなご質問ありがとうございます!
頂点のx座標とは、
式を平方完成したときのx部分の符号をチェンジしたものになります。
今回の式であれば平方完成すると
y=(x+3)^2-9
となっており、x部分の数は+3です。
なので、頂点のx座標は+3の符号をチェンジした―3をとるようにしてください!