【二次関数】x軸から切り取る線分の長さの求め方と公式！

\(x\)軸から切り取る線分の長さを求めなさい。

ん？切り取る線分ってどこのこと？？

と、困っている方に向けてサクッと解説していきます。

\(x\)軸から切り取る線分とは

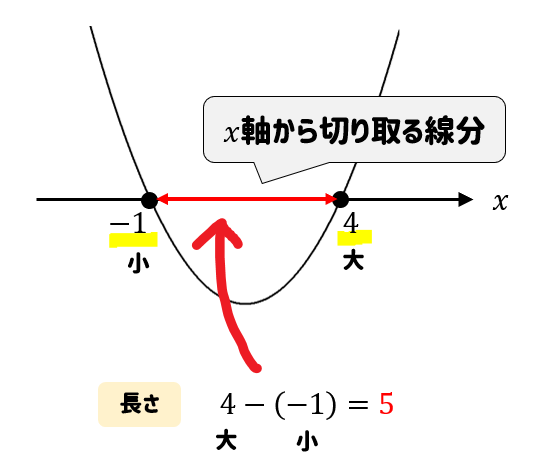
ここのことです。

長さの求め方は簡単で、\(x\)座標の大きいほうから小さいほうを引くと求めることができます。

一応、こういった公式を使って求めることもできるのですが

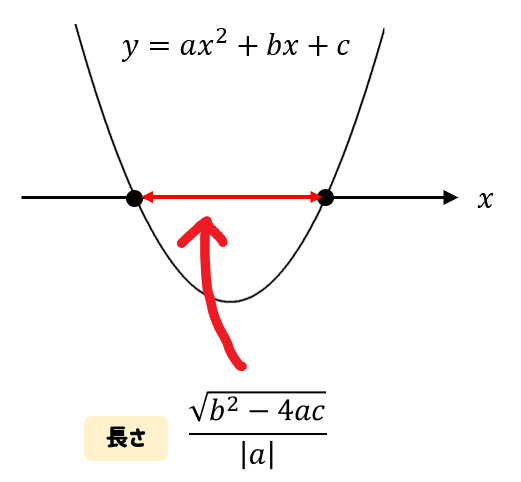
実際に問題を使いながら線分の長さを求める手順を確認してみましょう。

今回の内容はこちらの動画でも解説しています(‘◇’)ゞ

x軸から切り取る線分を求める手順

線分の長さを求めるためには、\(x\)軸との共有点の座標が必要です！

\(y=0\) を代入して、\(x\)軸との共有点の座標を求めましょう。

$$\begin{eqnarray}x^2-8x+12&=&0\\[5pt](x-6)(x-2)&=&0\\[5pt]x=2,6&& \end{eqnarray}$$

これで\(x\)軸との共有点が2，6と求まりましたね。

あとは、これを大きい方から小さい方を引けば完成です。

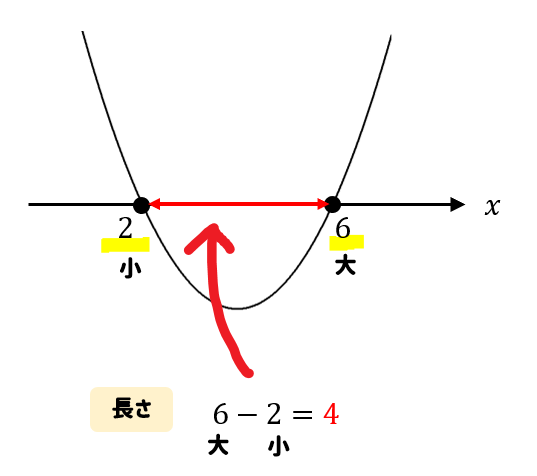
では、いろんなパターンについて確認してみましょう。

こちらの二次関数は\(x\)軸との共有点を求めるのが少しだけめんどうですw

解の公式を使って頑張って計算しましょう。

\(y=0\)を代入して、方程式を解いていくと

$$\begin{eqnarray}&&-2x^2-3x+3=0\\[5pt]&&2x^2+3x-3=0\\[5pt]&&x=\frac{-3\pm\sqrt{3^2-4\cdot 2\cdot (-3)}}{2\times2}\\[5pt]&&x=\frac{-3\pm \sqrt{33}}{4} \end{eqnarray}$$

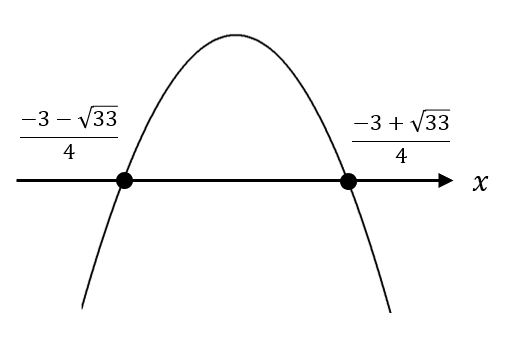
このような複雑な値になりました(^^;)

うぇ…なんだこの値、計算間違ってんじゃないかな、と不安になるかもしれません。

ですが、切り取る線分の問題ではこのようなルートが出てくる値の方が多いくらいです。

結局、計算方法は同じです。

大きい方から小さい方を引けばよいので

$$\begin{eqnarray}&&\frac{-3+ \sqrt{33}}{4}-\frac{-3- \sqrt{33}}{4}\\[5pt]&=&\frac{-3+ \sqrt{33}+3- \sqrt{33}}{4}\\[5pt]&=&\frac{2\sqrt{33}}{4}\\[5pt]&=&\frac{\sqrt{33}}{2}\cdots(解) \end{eqnarray}$$

このような計算になりました。

解の公式を使って、複雑な値が出てきましたが

線分を求めるためには引き算をするので

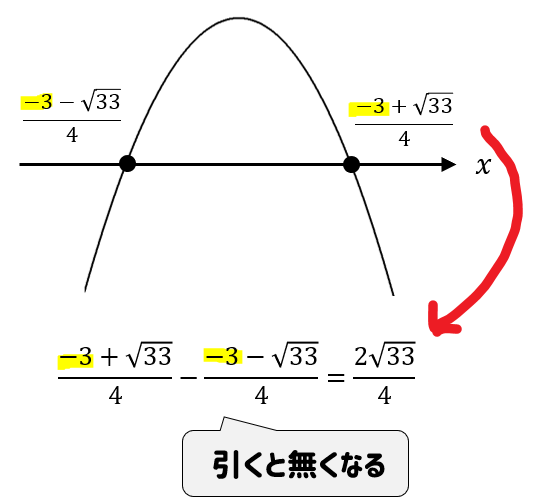
ここの数字の部分は必ず消えてしまいます。

なので、答えとしては少しだけスッキリとした形になりますね。

これはちょっと発展的な問題です。

まずは、線分の長さを表してみましょう。そのために、\(x\)軸との共有点を求めます。

$$\begin{eqnarray}x^2-(a+2)x+2a&=&0\\[5pt](x-2)(x-a)&=&0\\[5pt]x=2,a&& \end{eqnarray}$$

\(x\)軸との共有点が\(2,a\)だと求まりましたが、ちょっと困ったことが…

線分の長さを求めるためには、大きい方から小さい方を引けばよいのですが

\(2\)と\(a\)、どちらが大きいのか分からん！

ってなりますね。

このように大小関係がハッキリとしない場合には

$$\large{(線分の長さ)=|a-2|}$$

このように絶対値をつけることで解決します。

そして、この線分の長さが\(3\)になるということから次のような方程式ができあがります。

$$\begin{eqnarray}|a-2|&=&3\\[5pt]a-2&=&\pm3\\[5pt]a&=&5,-1\cdots(解) \end{eqnarray}$$

絶対値の計算が不安な方はこちらをどうぞ

⇒ 【苦手な人向け】絶対値の方程式、不等式の解き方をイチから解説！

公式を使って求めるやり方

このような公式を使って求めることもできます。

が、結局は上で紹介してきた手順を少しだけショートカットしているだけのものなので、別に覚える必要はないかなと思います。

一応紹介だけ。

これを公式に当てはめて計算してみると

$$\begin{eqnarray}&&\frac{\sqrt{(-8)^2-4\cdot 1\cdot 12}}{|1|}\\[5pt]&=&\sqrt{64-48}\\[5pt]&=&\sqrt{16}\\[5pt]&=&4\cdots(解) \end{eqnarray}$$

このように計算できます。

場合によっては公式を使うことによって時間がかかってしまう場合もあるので注意だね(^^;)

まとめ！

共有点の座標を大きい方から小さい方を引く！

大小が分からない場合には絶対値をつけて引く！

ルートがでてきて複雑な値になることがありますが、最終的にはちょっとだけスッキリした形になるぞ！

ってことで、今回は以上。

たくさん練習して解けるようにしておこうね(/・ω・)/