高校数学で学習する「逆・裏・対偶」の作り方について
問題を使って具体的に解説していきます。
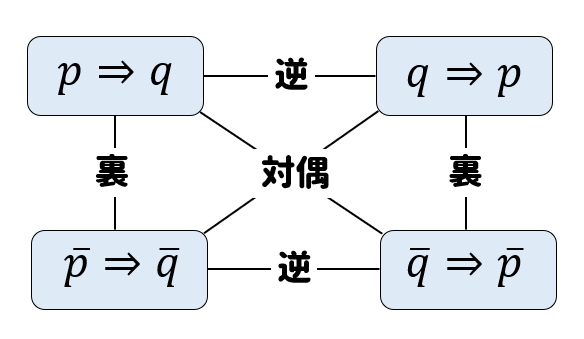
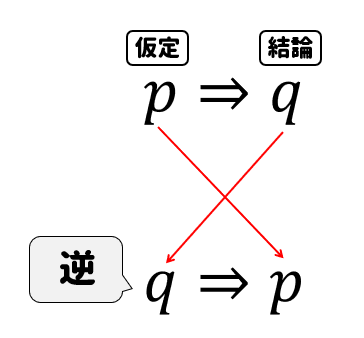
逆の作り方
逆とは、仮定と結論を入れかえたものです。
【問題】
次の命題の逆を述べなさい。
\(x=3\) ならば、\(x^2=9\)である。
逆の作り方は簡単！
仮定と結論をひっくり返すだけでOKです。
よって
$$【逆】x^2=9 ならば、x=3である。\cdots(解)$$
となります。
ちなみに、元の命題は真でしたが、逆は偽になっています。
このように、逆を作った場合
必ずしも元の命題と真偽が一致するわけではありません。
裏の作り方
裏とは、仮定と結論を否定の形にしたものです。
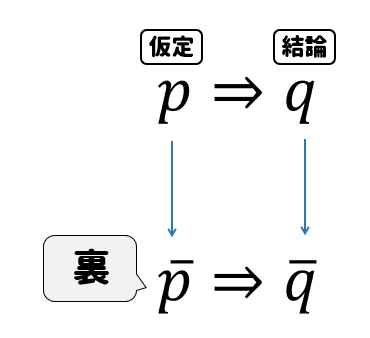
その名の通り、仮定と結論の条件を裏返したものです。
ここでポイントとなるのが、否定の作り方です。
いくつか確認しておきましょう。
【否定の作り方】
- 「である」の否定は「でない」
\(x\)は3の倍数であるの否定 ⇒ \(x\)は3の倍数でない。
\(x\)は偶数であるの否定 ⇒ \(x\)は奇数である。
※偶数⇔奇数のように反対の意味を表す語がある場合には利用する。
- 「\(＝\)」の否定は「\(\neq\)」にする。
\(x=3\)の否定 ⇒ \(x\neq 3\)
- 不等号の否定は逆にする。
\(x>3\)の否定 ⇒ \(x≦3\)
不等号の向きを逆、イコールがなければつける。
- 「かつ」⇔「または」
\(x=2\) かつ \(y=3\)の否定 ⇒ \(x\neq 2\) または \(y\neq 3\)
それぞれの条件の否定を作り、「かつ」を「または」に変える。
では、否定の作り方を確認したところで
裏の作り方について問題を見ていきましょう。
【問題】
次の命題の裏を述べなさい。
\(x+y>3\) ならば、\(x>2\)または\(y>1\)である。
まず、仮定と結論の否定を考えましょう。
\(x+y>3\)の否定は、\(x+y≦3\)
\(x>2\)または\(y>1\)の否定は、\(x≦2\)かつ\(y≦1\)
よって、
$$【裏】x+y≦3 ならば、x≦2かつy≦1である。\cdots(解)$$
となります。
対偶の作り方
対偶とは、仮定と結論の否定をひっくり返したものです。
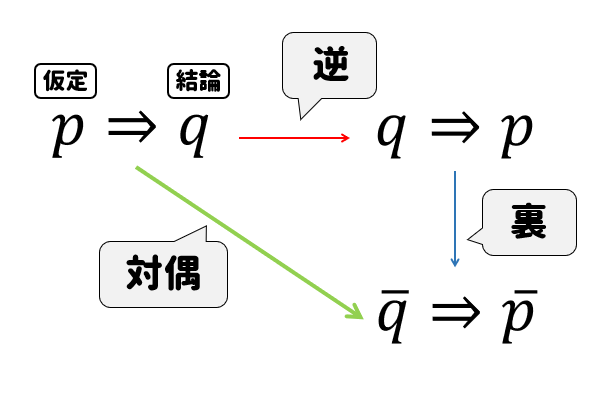
つまり、逆を裏にしたものです。
裏を逆にしたものとも考えれますが、どちらでもよいです。
対偶を扱う上で絶対に覚えておきたい特徴があります。
それは…
命題の真偽と対偶の真偽は一致する。
ということです。
命題の真偽が判断しにくい場合には、対偶を作り
その対偶の真偽を調べることによって
もとの命題の真偽を求めるということもできます。
【問題】
次の命題の裏を述べなさい。
\(a\neq 0\)または\(b\neq 0\) ならば、\(ab\neq 0\)である。
対偶とは、逆を裏にしたものですから
まずは逆の形を作りましょう。
$$ab\neq 0ならば、a\neq 0またはb\neq 0である。$$
では、これを裏にすることによって対偶の完成となります。
$$【対偶】ab =0ならば、a= 0かつb= 0である。\cdots(解)$$
ちなみに、この対偶は反例\(a=1, b=0\) によって偽となりますので
もとの命題も偽ということになります。
まとめ！
問題などで出題される場合には対偶を問われることがほとんどです。
対偶は命題と真偽が一致することから
証明問題に利用されることもあります。
それだけ対偶には使い道があるということなので
しっかりと作り方を覚えておきたいですね！
コメントを残す