二次関数 kaztastudy

【平方完成】文字を含む式の場合は？やり方を丁寧に解説！




今回は、数学Ⅰで学習する二次関数の単元から『文字を含む式を平方完成する方法』について解説していきます！

文字を含む式というのは、次のようなものになります。

$$\large{y=x^2-4ax+2a^2+5a-3}$$

模試やセンター試験などの入試レベルの問題になると、二次関数の式に文字が含まれていることが多くなります。

そうなると、こういった複雑な式であっても軽々と平方完成することができなければいけません。

 

ということで、今回は文字を含む式の平方完成について練習していきましょう！

 

今回の内容は式変形が複雑なところもあるので、動きのある動画講義をチェックしていただけると理解が早いですよ＾＾

平方完成のやり方

まずは、平方完成のやり方について確認しておきましょう。

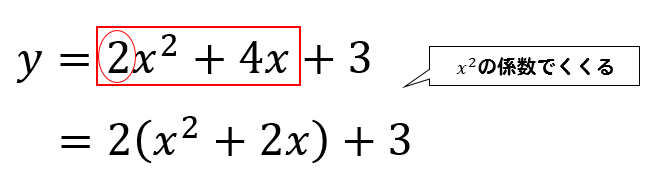
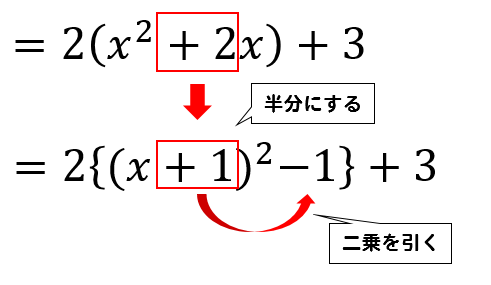
平方完成の手順

  1. \(x^2\)の係数でくくる
  2. 半分にする
  3. 2乗を引く

 

この3ステップでしたね！

文字を含む式であっても、この手順に従って平方完成をおこなっていきます。

文字を含む式の平方完成

$$\large{y=x^2-4ax+2a^2+5a-3}$$

それでは、この式を平方完成していきましょう。

ステップ①～\(x^2\)の係数をくくる～

今回の式では、\(x^2\)の係数は１なので、くくりだす必要はありませんね。

ステップ②③～半分にして、2乗を引く～

次は、\(x\)の係数を半分にして2乗を引きましょう。

 

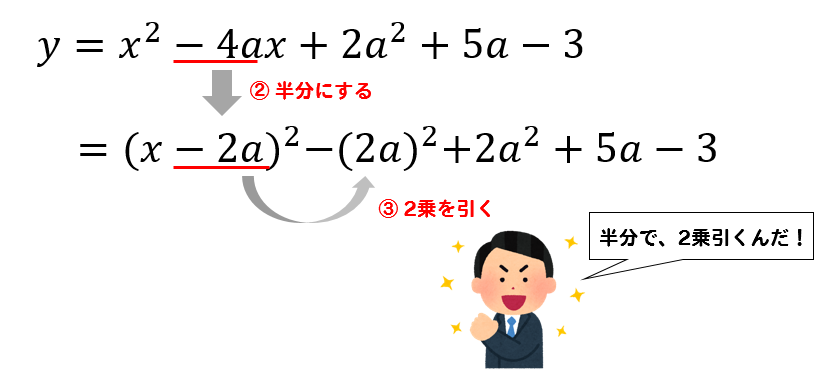
あとは、計算していけばOKですね。

$$y=x^2-4ax+2a^2+5a-3$$

$$=(x-2a)^2-(2a)^2+2a^2+5a-3$$

$$=(x-2a)^2-4a^2+2a^2+5a-3$$

$$=(x-2a)^2-2a^2+5a-3$$

これで完成となります！

ちなみに、頂点は\((2a,  -2a^2+5a-3)\)ですね。

 

それでは、他にも文字を含む式を平方完成してみましょう！

 

いろんなパターンの式を平方完成してみよう！

$$\large{y=-2x^2+2ax-\frac{5}{4}a^2+2a-1}$$

平方完成のやり方はこちら

 

$$y=-2x^2+2ax-\frac{5}{4}a^2+2a-1$$

$$=-2(x^2-ax)-\frac{5}{4}a^2+2a-1$$

$$=-2\left\{ \left( x-\frac{a}{2}\right)^2-\frac{a^2}{4}\right\}-\frac{5}{4}a^2+2a-1$$
$$=-2\left(x-\frac{a}{2}\right)^2-\frac{a^2}{4}\times (-2)-\frac{5}{4}a^2+2a-1$$
$$=-2\left(x-\frac{a}{2}\right)^2+\frac{a^2}{2}-\frac{5}{4}a^2+2a-1$$
$$=-2\left(x-\frac{a}{2}\right)^2-\frac{3}{4}a^2+2a-1$$

 

頂点は、\(\displaystyle{\left(\frac{a}{2},  -\frac{3}{4}a^2+2a-1\right)}\)となります。

 

 

$$\large{y=x^2-(a+1)x+a+2}$$

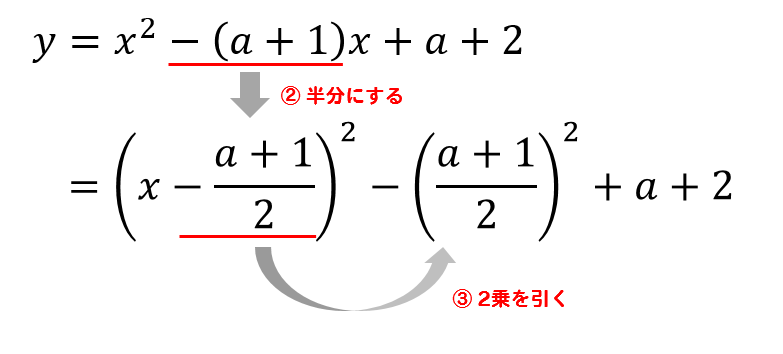
平方完成のやり方はこちら

 

$$y=x^2-(a+1)x+a+2$$

$$=\left( x-\frac{a+1}{2}\right)^2-\left(\frac{a+1}{2}\right)^2+a+2$$
$$=\left( x-\frac{a+1}{2}\right)^2-\frac{a^2+2a+1}{4}+\frac{4a+8}{4}$$
$$=\left( x-\frac{a+1}{2}\right)^2+\frac{-a^2+2a+7}{4}$$

 

頂点は、\(\displaystyle{\left(\frac{a+1}{2},  \frac{-a^2+2a+7}{4}\right)}\)となります。

 

 

$$\large{y=-x^2+(a-2)x-\frac{a^2}{4}+2a}$$

平方完成のやり方はこちら

 

$$y=-x^2+(a-2)x-\frac{a^2}{4}+2a$$

$$=-\left\{x^2-(a-2)x\right\}-\frac{a^2}{4}+2a$$
$$=-\left\{ \left( x-\frac{a-2}{2}\right)^2-\frac{a^2-4a+4}{4}\right\}-\frac{a^2}{4}+2a$$
$$=-\left( x-\frac{a-2}{2}\right)^2+\frac{a^2-4a+4}{4}-\frac{a^2}{4}+\frac{8a}{4}$$

$$=-\left( x-\frac{a-2}{2}\right)^2+a+1$$

 

頂点は、\(\displaystyle{\left(\frac{a-2}{2},  a+1\right)}\)となります。

 

文字を含む式の平方完成　まとめ

お疲れ様でした！

文字を含む式の平方完成は、途中式が複雑になってしまいますが手順は基本通りです。

しっかりと手順に沿って、丁寧に計算していけば解けるはずです(^^)

 

たくさん練習して、スラスラ解けるようにしておきましょう！

分数をくくりだすような平方完成はこちらで練習しておきましょう(^^)

＞＞＞【平方完成】分数でくくるパターンの問題の解き方を解説！

 

こちらの記事も合わせてどうぞ！

 

数学の成績が落ちてきた…と焦っていませんか？

数スタのメルマガ講座（中学生）では、
以下の内容を無料でお届けします！
メルマガ講座の内容

① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！

今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！

 
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
講座を無料で受講する！
 
 

数スタの他記事はこちらから



こちらの関連記事はいかがでしょうか？

コメントを残す

メールアドレスが公開されることはありません。

RECOMMENDこちらの記事も人気です。