今回は高校数学Ⅰで学習する『三角比』の単元から、90ｰθの考え方・覚え方について解説していくよ！
90-θといえば、次のような変形があるよね
$$\sin (90°-\theta)=\cos\theta$$
$$\cos (90°-\theta)=\sin\theta$$
$$\tan (90°-\theta)=\frac{1}{\tan\theta}$$
これがね…
なかなか覚えれないんすよ！！
\(\sin\)が\(\cos\)に変わったり、\(\tan\)に関しては分数になっちゃうし…
というわけで、今回の記事では90ｰθの変形について詳しく見ていこう！
三角比 90ｰθの考え方！
90ｰθとは何のことを言っているのか…
ここが分かりにくいところなのでハッキリとさせておきましょう。
θという角を持つ直角三角形を考えたとき
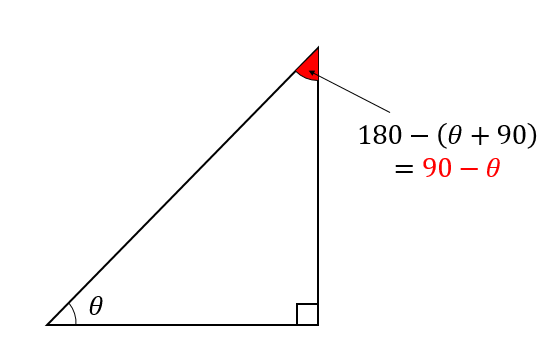
このように、直角ではないもう一方の角が90ｰθになっているのです。
それでは、この直角三角形において
θに着目した三角比の値と
90ｰθに着目した三角比の値をそれぞれ考えてみましょう。
まずは、θに着目した場合
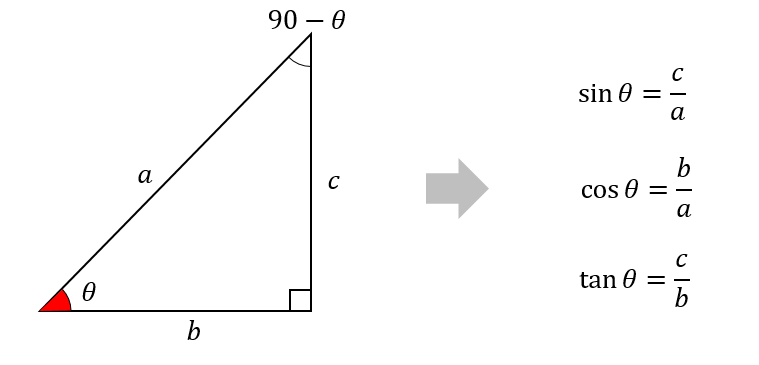
それぞれの値は上のようになります。
次に90ｰθの着目した場合
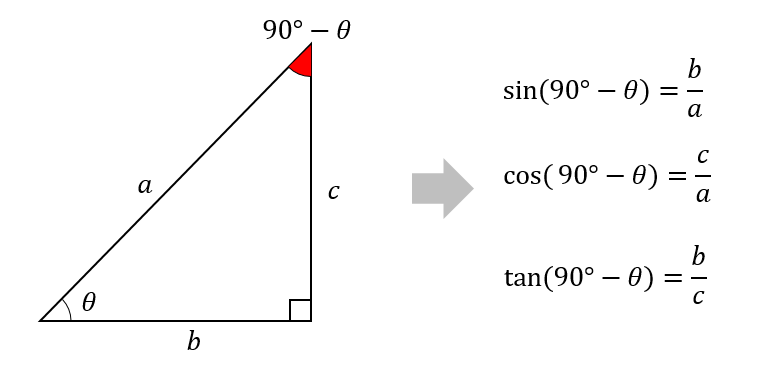
それぞれこのような値になります。
90ｰθが上にあって、三角比の値が分かりにくいという方は
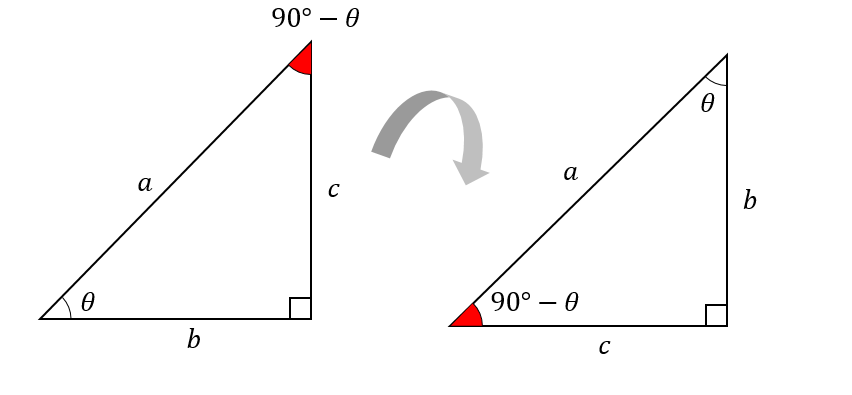
このように90ｰθの角が左下になるように三角形をずらして考えてみるといいですね(^^)
すると
θと90ｰθの三角比の値をそれぞれ比べてみると…
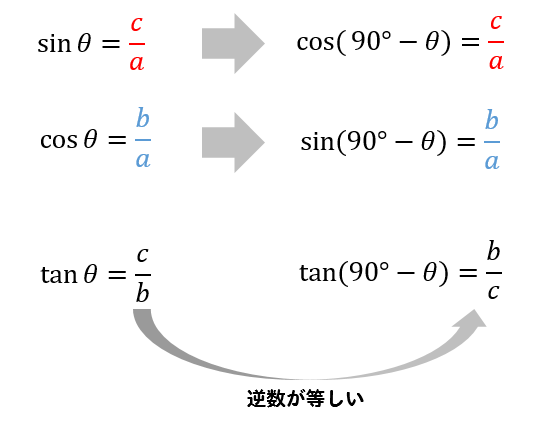
このように
$$\sin (90°-\theta)=\cos\theta$$
$$\cos (90°-\theta)=\sin\theta$$
$$\tan (90°-\theta)=\frac{1}{\tan\theta}$$
となっていることが分かりますね！
よって
90ｰθの変形を忘れてしまった場合には、このように直角三角形を書いて見比べてみると思い出すことができますね(^^)
三角比 90-θの覚え方！
さて、直角三角形を書いて見比べることで自分で変形を導くことができるものの…
やっぱり覚えるのは面倒だぞ…
そういう方は数学Ⅱで学習する『加法定理』というものを活用することで、変形を導いてやることができます。
加法定理とは以下のようなものでした。
（まだ加法定理を習っていない1年生はごめんなさい…）
この加法定理を使ってやると
$$\sin(90°-\theta)=\sin 90°\cos\theta-\cos 90°\sin\theta$$
$$=1\times \cos\theta-0\times \sin\theta$$
$$=\cos\theta$$
$$\cos(90°-\theta)=\cos 90°\cos\theta+\sin 90°\sin\theta$$
$$=0\times \cos\theta+1\times \sin\theta$$
$$=\sin\theta$$
このように導くことができますね！
\(\tan(90°-\theta)\)に関しては
\(\tan 90°\)の値が無いので、加法定理はちょっと使えないね…
だけど、相互関係である
$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$
を使って考えると…
$$\tan(90°-\theta)=\frac{\sin(90°-\theta)}{\cos(90°-\theta)}$$
$$=\frac{\cos\theta}{\sin\theta}$$
$$=\frac{1}{\frac{\sin\theta}{\cos\theta}}$$
$$=\frac{1}{\tan\theta}$$
このように導いてあげることはできます。
だけど、ちょっと複雑かな…？
\(\tan(90°-\theta)\)の変形がどうしても思い出せない…
というときの保険として覚えておくくらいで良いかもしれませんね。
練習問題に挑戦してみよう！
それでは、90ｰθの変形について練習問題に挑戦してみましょう。
次の三角比を45°以下の鋭角の三角比で表せ
$$(1) \cos 75°$$
$$(2) \sin 80°$$
$$(3) \tan 65°$$
演習問題の解答＆解説
それぞれ90ｰθの形で表すことがポイントです。
$$75°=90°-15°$$
$$80°=90°-10°$$
$$65°=90°-25°$$
それぞれこのように表すことができるので
$$(1) \cos 75°=\cos(90°-15°)=\sin 15°$$
$$(2) \sin 80°=\sin(90°-10°)=\cos 10°$$
$$(3) \tan 65°=\tan(90°-25°)=\frac{1}{\tan 25°}$$
以上のように変形することができます。
まとめ
お疲れ様でした！
これで90ｰθの変形はバッチリでしょうか？
この変形は問題で問われることも少ないです。
そのため、突然問われると…
あれ？どうだっけ(^^;
と、なってしまいがちです。
そういうときには、直角三角形を書いて見比べてみたり、加法定理を使って自ら変形を導けるようにしておきましょう！
数学が得意な方でもこの変形をスパッと言える人は多くないです。
みんな、その場で変形を導けるようにしているからですね。
実際に、私もすぐには言えなかったりするかも…(^^;
中学生向けの英文法サイトを開設！
≫ 中学英語の文法まとめサイト！