今回は、図形の単元から
『円周の長さを求める方法』について解説していくよ!
- 円周の長さを求める公式ってなんだっけ?
- そもそも、円周率ってなんだ?
- 計算方法ができない…
そういった悩みが解決できるように解説していくのでこの記事を通して理解を深めていきましょう(^^)
円周率とは
円の公式を扱うときに、円周率というものが出てくるよね。
$$\LARGE{3.1415 \ldots}$$
こういうやつだね。
多くの方が、小学生のときに習っていて見覚えはあるかと思います。
それじゃ、円周率ってなに??って聞かれると

え、それは…3.14でしょ…?
とくらいしか答えられないのではないでしょうか。
この円周率というものは何を表した数値なのかと言うと
『円周の長さは、直径の3.14倍くらいですよ』
ってことを表したモノなんだよね。
つまり、直径が2㎝だったら円周の長さは
$$\LARGE{2\times 3.14=6.28 cm}$$
ということになるね。
円周の長さの公式
円周率の意味を理解していれば、円周の長さを求める公式はバッチリのはず!
(円周の長さ)=(直径)×(円周率)
このように表してあげることができます。
直径の長さに円周率である3.14を掛け算するだけでOK
簡単ですね(^^)
中学生では\(\pi\)を使う!
さて、ここまでは小学生バージョンでお話を進めてきました。
何が小学生バージョンだったのかというと
円周率を3.14と表すことですね。
中学生では、この円周率3.14を\(\pi\)という記号を使って表すことになります。
\(\pi\)というのはギリシア文字で円周という意味を表す「ペリメトロス」という言葉の頭文字から取られているようです。
そして、円周の長さを求める公式は以下のように習うことが多いです。
(円周の長さ)=2×(半径)× \(\pi\)
あれ?
直径じゃないの!?

と思っちゃいますが
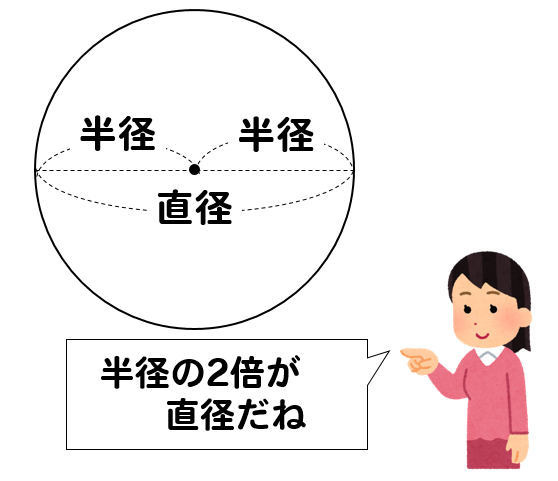
2×(半径)というのが直径を表したモノになります。
別にさ
(円周の長さ)=(直径)× \(\pi\)
コレで良くない?と言いたいところですが
中学生の円に関する問題では、半径の値を基準に考えていくことが多いので公式も半径を使って表しておいた方が便利なんだよね。
ってことで、認識しておいてください(^^;
円周の長さの公式
(円周の長さ)=(直径)× \(\pi\)
(円周の長さ)=2×(半径)× \(\pi\)
まぁ、どちらで覚えてもらってもOKですよ
直径から円周の長さを求めてみよう!
それでは、次の図形の円周の長さを求めてみましょう。
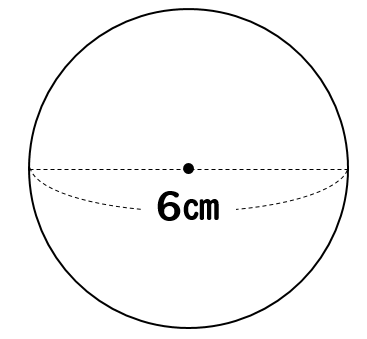
公式に当てはめて考えてみよう!
直径が6㎝なので
$$\LARGE{6\times 3.14=18.84 cm}$$
もしくは
$$\LARGE{6\times \pi=6\pi cm}$$
となります。
次は、半径が与えられている円で考えてみましょう。
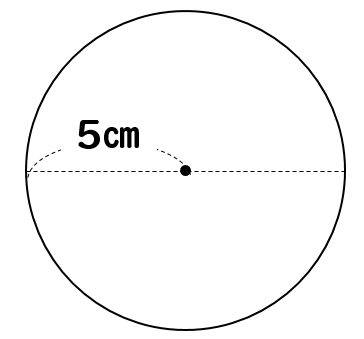
半径が5㎝なので、直径は2倍の10㎝ということになりますね。
$$\LARGE{10\times 3.14=31.4 cm}$$
もしくは
$$\LARGE{2\times 5\times \pi=10\pi cm}$$
ということになります(^^)
計算も簡単ですね!

円周の長さから直径を求めるには??
直径から円周の長さを求める方法については上でマスターしてもらいましたが、その逆である円周の長さから直径を求める方法についてはどうでしょうか?
こちらもよく出題される問題の1つです。
特に難しい話ではないので、かるーくマスターしちゃいましょ!
等式の性質を利用して、先ほどの円周の長さ公式を変形してみると
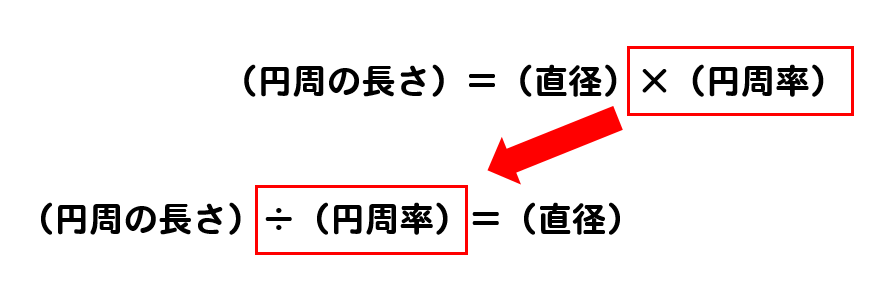
このようになっちゃいます。
つまり、直径の長さを求めたいときには
(円周の長さ)÷(円周率)
これを計算すればOKということになります。
公式っていうほどでもありませんが、覚えておくと便利かもしれません。
では、具体例を見ていきましょう。
(円周の長さ)÷(円周率)を計算すれば良いのだから
$$\LARGE{25.12\div 3.14=8}$$
よって、直径は8㎝ということが分かります。
中学生バージョンも見ておきましょう。
(円周の長さ)÷(円周率)を計算すれば良いのだから
$$\LARGE{12\pi\div \pi=12}$$
よって、直径は12㎝ということが分かります。
中学生バージョンの場合、\(\pi\)を取ってしまうだけの計算なので暗算でも大丈夫そうですね(^^)
演習問題に挑戦!
それでは、理解を深めるために演習問題に挑戦してみましょう!
まとめ
お疲れ様でした!
最後に円周の長さの公式を確認しておきましょう。
円周の長さの公式小学生バージョン
(直径)×(円周率3.14)
中学生バージョン
(直径)× \(\pi\)
2×(半径)× \(\pi\)
円周の長さから直径を求める公式小学生バージョン
(円周の長さ)÷(円周率3.14)
中学生バージョン
(円周の長さ)÷(円周率\(\pi\))
以上!
今後もいろんな場面で活用していく公式になるからしっかりと覚えておこうね。
ファイトだー(/・ω・)/


















分かりやすい 孫たちにも教えられる
ありがとうございました。