【二次関数】頂点の求め方、公式は？問題を使ってイチから解説するぞ！

今回は高校数学Ⅰで学習する二次関数の単元から

頂点を求める方法

について解説していきます。

二次関数の頂点を求めるためには、平方完成という計算が必要になります。

この平方完成がひじょーにメンドイよね(^^;)

分数やマイナスなどが式に含まれていると、計算が複雑になるし…

というわけで、今回の記事では

平方完成をせずに頂点を求める公式は？

平方完成をする場合にはどのようにする？

について、イチから解説していきます。

平方完成のやり方についてはこちらの動画でも解説しています！

動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾

高校メルマガ講座の無料登録はこちら！

Contents

【二次関数の頂点】平方完成のやり方は？
【二次関数の頂点】求めるための公式は？？
【二次関数の頂点】式に分数がある場合には？
【二次関数の頂点】式にマイナスがある場合には？
【二次関数の頂点】練習問題！
【二次関数の頂点】まとめ！

【二次関数の頂点】平方完成のやり方は？

二次関数の頂点は、式を次のように表すことで求めることができます。

二次関数の頂点

$$y=a(x-p)^2+q$$

頂点 $(p, q)$ 軸 $x=p$

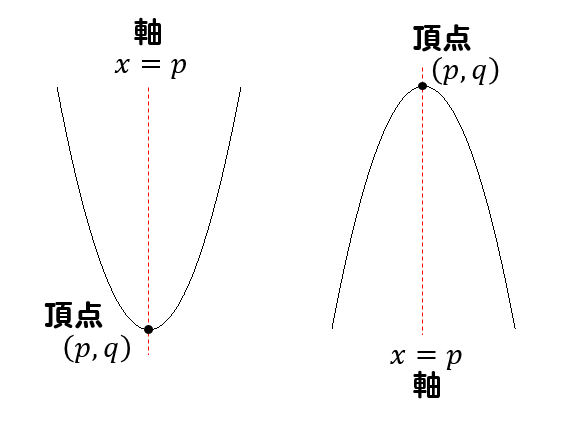
では、二次関数の式を$y=a(x-p)^2+q$ の形にするためには、どのような計算をしていけばよいのでしょうか。

次の二次関数を例に、平方完成のやり方を確認しておきましょう。

次の二次関数の頂点を求めなさい。

$$y=2x^2+4x+3$$

平方完成の手順

$x^2$の係数で、$x^2$と$x$の項をくくってやります。

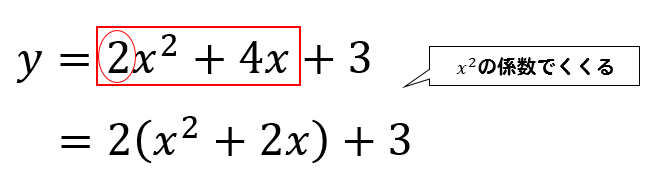
$x$の項の係数を半分にして、その数の二乗を引きます。

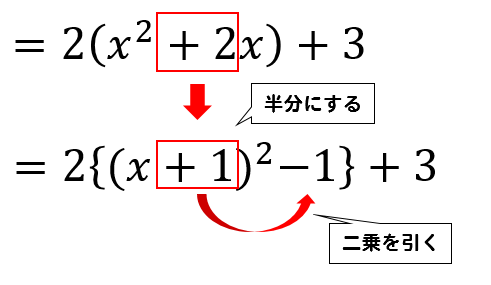
くくっていた数を分配法則で計算してやれば完成！

以上より、$y=2x^2+4x+3$ の頂点は$(-1,1)$、軸は$x=-1$ だと分かりました。

二次関数の頂点は、上で紹介したような手順で求めることができます。

すこし計算が複雑ではあるんだけど、そこはたくさん練習してカバーしていこう！

いやいや…こんな複雑な手順やりたくないんですけど…

もうちょっとラクにできませんか？

という方は、次の章にて平方完成をせずに頂点を求める方法について紹介しておきます。

平方完成の手順をもう少し練習したいぜ！

という方は最後の章に演習問題を用意しておきますね(^^)

【二次関数の頂点】求めるための公式は？？

平方完成なんてやってらんねぇ…って方は次の公式を覚えておくといいでしょう。

二次関数の頂点を求める公式

$$y=ax^2+bx+c$$

$$頂点 \left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a} \right)$$

$$軸 x=-\frac{b}{2a}$$

この公式に、二次関数の係数を代入することで頂点を求めることができます。

では、次の二次関数の頂点を公式を用いて求めてみましょう。

次の二次関数の頂点を求めなさい。

$$y=2x^2+4x+3$$

二次関数の式から、$a=2, b=4, c=3$ となります。これを用いて

$$-\frac{b}{2a}=-\frac{4}{2\cdot 2}=-1$$

$$-\frac{b^2-4ac}{4a}=-\frac{4^2-4\cdot 2\cdot 3}{4\cdot 2}=1$$

よって、頂点は$(-1, 1)$、軸は $x=-1$ となります。

先ほどの複雑だった平方完成に比べたら、かなりラクになりましたね！

だけど、いくら平方完成がメンドイからといっても、やはり手順は身につけておくべきです。

この公式を使って頂点を求める場合であっても、必ず平方完成の手順は理解しておくようにしましょう。

実際に、この公式だって次のような平方完成によって導かれているわけだからね(^^)

$$\begin{eqnarray}ax^2+bx+c&=&a\left( x^2+\frac{b}{a}x \right) +c\\[5pt]&=&a\left( x+\frac{b}{2a}\right)^2-a\left(\frac{b}{2a} \right)^2+c\\[5pt]&=&a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a} \end{eqnarray}$$

【二次関数の頂点】式に分数がある場合には？

ここからは、平方完成を用いて頂点を求める場合について解説していきます。

次の関数の頂点を求めなさい。

$$y=\frac{2}{3}x^2-2x+3$$

分数がある場合には、難易度がぐっと高くなりますね。

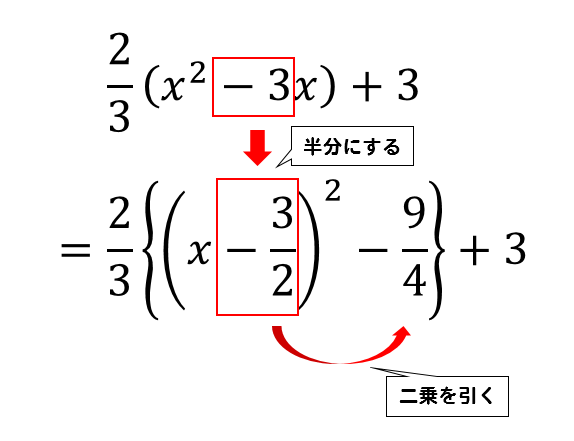
今回の場合では、$x^2$ の係数である$\displaystyle{\frac{2}{3}}$ でくくりだす必要があります。

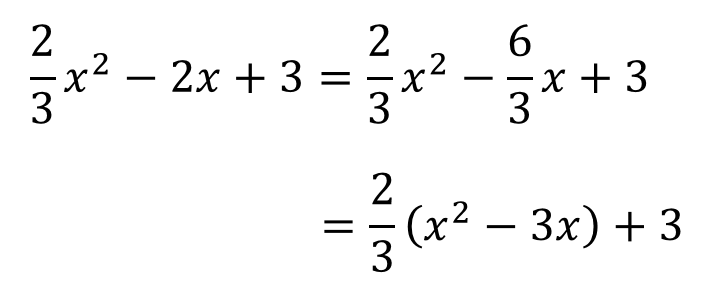
こんな感じです。

分数でくくりだすときには、一方の数も分数の形で表し通分してやると分かりやすくなります。

くくりだしができたら、あとは今までと同じ手順でやっていけばOK！

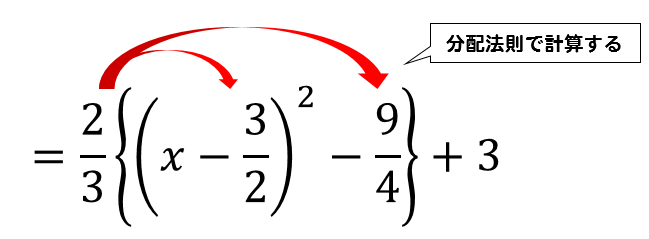
$$=\frac{2}{3} \left( x-\frac{3}{2} \right)^2-\frac{9}{4}\times \frac{2}{3}+3$$

$$=\frac{2}{3} \left( x-\frac{3}{2} \right)^2-\frac{3}{2}+3$$

$$=\frac{2}{3} \left( x-\frac{3}{2} \right)^2-\frac{3}{2}+\frac{6}{2}$$

$$=\frac{2}{3} \left( x-\frac{3}{2} \right)^2+\frac{3}{2}$$

よって、二次関数の頂点は、$\displaystyle{\left(\frac{3}{2}, \frac{3}{2}\right)}$ となります。

分数の平方完成について、もっと詳しく知りたい方はこちらの記事をご参考に！

＞【平方完成】分数でくくるパターンの問題の解き方を解説！

【二次関数の頂点】式にマイナスがある場合には？

次は、$x^2$の係数がマイナスになっている場合の平方完成をやっておきましょう。

次の関数の頂点を求めなさい。

$$y=-2x^2+8x-1$$

$x^2$の係数がマイナスになっている場合には、マイナスの符号ごとくくりだしていく必要があります。

$$\begin{eqnarray}y&=&-2x^2+8x-1\\[5pt]&=&-2(x^2-4x)-1 \end{eqnarray}$$

このように、マイナスでくくるとかっこ内の符号が変わってしまうので気を付けてくださいね。

その後は、今まで同じ手順で平方完成をやっていけばOKです。

$$\begin{eqnarray}y&=&-2x^2+8x-1\\[5pt]&=&-2(x^2-4x)-1 \\[5pt]&=&-2\{(x-2)^2-4\}-1\\[5pt]&=&-2(x-2)^2+7\end{eqnarray}$$

以上より、頂点は$(2,7)$ ということが分かります。

マイナスでのくくりだしは、符号ミスが多発してしまうので気を付けましょう！

【二次関数の頂点】練習問題！

次の二次関数の頂点を求めなさい。

$$y=x^2-2x-2$$

解説＆答えはこちら

答え

$$(1,-3)$$

$$\begin{eqnarray}y&=&x^2-2x-2\\[5pt]&=&(x-1)^2-1-2\\[5pt]&=&(x-1)^2-3 \end{eqnarray}$$

次の二次関数の頂点を求めなさい。

$$y=2x^2-8x-3$$

解説＆答えはこちら

答え

$$(2,-11)$$

$$\begin{eqnarray}y&=&2x^2-8x-3\\[5pt]&=&2(x^2-4x)-3\\[5pt]&=&2\{(x-2)^2-4\}-3\\[5pt]&=&2(x-2)^2-11 \end{eqnarray}$$

次の二次関数の頂点を求めなさい。

$$y=-2x^2+6x-1$$

解説＆答えはこちら

答え

$$\left( \frac{3}{2},\frac{7}{2} \right)$$

$$\begin{eqnarray}y&=&-2x^2+6x-1\\[5pt]&=&-2(x^2-3x)-1\\[5pt]&=&-2\{(x-\frac{3}{2})^2-\frac{9}{4}\}-1\\[5pt]&=&-2(x-\frac{3}{2})^2+\frac{7}{2} \end{eqnarray}$$

次の二次関数の頂点を求めなさい。

$$y=\frac{1}{2}x^2+x$$

解説＆答えはこちら

答え

$$\left( -1,-\frac{1}{2} \right)$$

$$\begin{eqnarray}y&=&\frac{1}{2}x^2+x\\[5pt]&=&\frac{1}{2}(x^2+2x)\\[5pt]&=&\frac{1}{2}\{(x+1)^2-1\}\\[5pt]&=&\frac{1}{2}(x+1)^2-\frac{1}{2} \end{eqnarray}$$