高校数学Ⅰで学習する関数の単元から
「2次関数の文章題」
についての問題をパターン別にまとめていきます。
それぞれの問題には解説動画をつけているので、わかりづらいところは動画でチェックしてみてください^^
二次関数の文章題(面積、平方など)
問題①針金を使って面積を考える
【問題】
長さ\(16\)㎝の針金を2本に切り,それぞれの針金を折り曲げて正方形を2つ作る。
これらの正方形の面積の和を最小にするには,針金を何㎝と何㎝に切ればよいか。
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
一方の針金を \(x\)㎝とすると、もう一方の針金は \((16-x)\)㎝と表すことができる。
ともに長さは正になることから
\(x>0\)、 \(16-x>0\) ⇒ \(16>x\)
よって、\(0<x<16\) となる。
\(x\)㎝の針金を正方形にすると、1辺が\(\frac{x}{4}\)㎝となる。
よって、面積は \(\left(\frac{x}{4} \right)^2=\frac{x^2}{16}\)
\((16-x)\)㎝の針金を正方形にすると、1辺が\(\frac{16-x}{4}\)㎝となる。
よって、面積は \(\left(\frac{16-x}{4} \right)^2=\frac{256-32x+x^2}{16}\)
正方形の面積の和を\(y\)㎡として考えると
$$\begin{eqnarray}y&=&\frac{x^2}{16}+ \frac{256-32x+x^2}{16}\\[5pt]&=&\frac{1}{8}x^2-2x+16\\[5pt]&=&\frac{1}{8}(x^2-16x)+16\\[5pt]&=&\frac{1}{8}(x-8)^2+8\end{eqnarray}$$
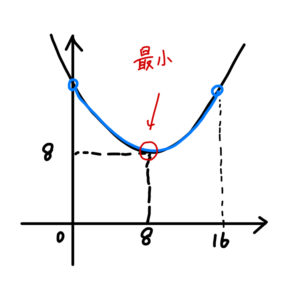
グラフより
\(x=8\) のとき最小値 \(8\) となる。
よって、針金は\(8\)㎝と\(8\)㎝に切ればよい。
問題②長方形の面積の最大
【問題】
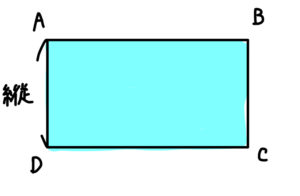
下の図のような長方形の作る。辺ABの部分をのぞく周囲の長さを\(8\)mとし,面積を最大にするには,縦の長さを何mにすればよいか。
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
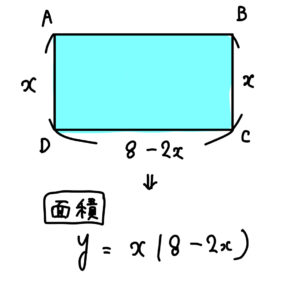
縦の長さを\(x\)m とすると、横の長さは \((8-2x)\)mと表せる。
ともに長さは正になるので、
\(x>0\), \(8-2x>0\) ⇒ \(x<4\)
よって、\(0<x<4\) となる。
長方形の面積を\(y\)㎡と考えると、
\(y=x(8-2x)\) と表せる。
$$\begin{eqnarray}y&=&x(8-2x)\\[5pt]&=&-2x^2+8x\\[5pt]&=&-2(x^2-4x)\\[5pt]&=&-2(x-2)^2+8 \end{eqnarray}$$
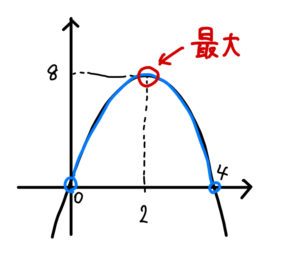
グラフより
\(x=2\) のとき最大値\(8\) となる。
よって、面積が最大となる縦の長さは\(2m\)
問題③直角三角形の中にある長方形
【問題】ニューアクションβより
下の図のように,\(BC=8\), \(AC=6\), \(∠C=90°\) の直角三角形ABCの辺AB上に点P,辺BC上に点Q,辺AC上に点Rをとり,長方形PQCRをつくるとき,この長方形の面積の最大値を求めよ。また、そのときのPQとPRの長さをそれぞれ求めよ。
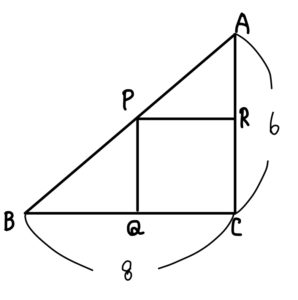
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
\(PQ=x\), \(PR=y\) とすると \(0<x<6\) となる。
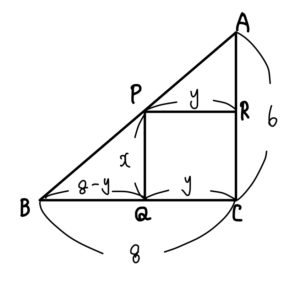
さらに、\(BQ=8-y\) と表せることから
平行線と線分の比を利用すると、\(AC:PQ=BC:BQ\) を利用すると
$$\begin{eqnarray}AC:PQ&=&BC:BQ\\[5pt]6:x&=&8:(8-y)\\[5pt]8x&=&-6y+48\\[5pt]y&=&-\frac{4}{3}x+8 \end{eqnarray}$$
となる。
長方形\(PQCR\) の面積を\(S\) として考えると
$$\begin{eqnarray}S&=&xy\\[5pt]&=&x\left(-\frac{4}{3}x+8\right)\\[5pt]&=&-\frac{4}{3}x^2+8x \\[5pt]&=&-\frac{4}{3}(x^2-6x)\\[5pt]&=&-\frac{4}{3}(x-3)^2+12\end{eqnarray}$$
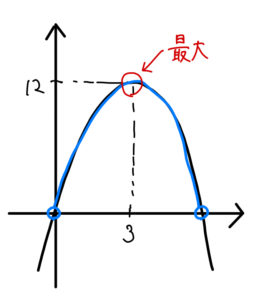
グラフより
\(x=3\) のとき最大値\(12\) となる。
\(x=3\) を \(y=-\frac{4}{3}x+8\) に代入すると \(y=4\) となる。
したがって
\(PQ=3\), \(PR=4\) のとき 最大値 \(12\) となる。
問題④売上金額の最大
【問題】ニューアクションβより
ある品物を1個60円で売ると1日に50個売れる。1個の値段を10円上げるごとに1日の売上個数は5個ずつ減るという。1個の値段をいくらにすれば1日の売上金額が最大になるか。また,そのときの売上金額はいくらか。
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
この問題では文字の置き方に注意!
「\(x\)円値上げる」と置いてしまうと式を作るのが難しくなります。
問題文より、10円ごとに条件が設定されているので、
10円を基準として、「\(10x\)円値上げする」と考えていきましょう。
1個の値段を\(10x\)円値上げすると、1個の値段は \((60+10x)\) 円と表せる。
売上個数は \(5x\) 個減ることになるので、\((50-5x)\)個となる。
\(x≧0\), \(50-5x≧0\) ⇒ \(10≧x\) であることから \(0≦x≦10\) となる。
売上金額を \(y\) 円とすると
$$\begin{eqnarray}y&=&(60+10x)(50-5x)\\[5pt]&=&-50x^2+200x+3000\\[5pt]&=&-50(x-2)^2+3200 \end{eqnarray}$$

グラフより
\(x=2\) のとき最大値 \(3200\) になる。
\(x=2\) ということは\(20\)円値上げということなので
したがって
1個の値段は\(80\)円、売上金額は\(3200\)円となる。
問題⑤平方の最大・最小
【問題】青チャートより
直角を挟む2辺の長さの和が\(20\) である直角三角形において,斜辺の長さが最小の直角三角形を求め,その斜辺の長さを求めよ。
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
直角を挟む2辺のうち一方の長さを\(x\) とすると、もう一方は \((20-x)\) と表せる。
長さはともに正になるので
\(x>0\), \(20-x>0\) ⇒ \(20>x\)
よって、\(0<x<20\) となる。
斜辺の長さを \(l\) とすると、三平方の定理より
$$\begin{eqnarray}l^2&=&x^2+(20-x)^2\\[5pt]&=&2x^2-40x+400\\[5pt]&=&2(x^2-20x)+400\\[5pt]&=&2(x-10)^2-+200 \end{eqnarray}$$
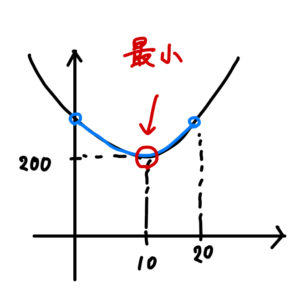
グラフより
\(x=10\) のとき \(l^2\) の最小値は \(200\) となる。
\(l>0\) だから \(l^2\) が最小となるとき \(l\) も最小となる。
\(l^2=200\) ⇒ \(l=\sqrt{200}=10\sqrt{2}\)
したがって
直角を挟む2辺の長さがともに \(10\)の直角二等辺三角形で、斜辺の長さは \(10\sqrt{2}\) となる。
まとめ!
お疲れ様でした!
二次関数の文章題をパターン別にまとめてみました。
初見では解くのが難しい問題もありますが、
たくさんの問題に触れ、知識の引き出しを増やしておくことが大切です。
何を文字で置けばよいのか。
そのときの範囲はどうなるのか。
変域に注意しながらグラフをかくとどうなるか。
この辺りを意識しながら、たくさん問題を解いていってくださいね!
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ! ←今回の記事
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















いいと思いました
ありがとうございます!!
長方形の問題の横の長さは8-2xではなく、4-xになりませんか?
8-2xは横の長さ2本分なので2でわる必要がありませんか?
これは問題文がちょっとイジワルなんですが、
「辺ABの部分をのぞく周囲の長さを8mとし」
とあるので、横の長さは8-2xでOKになります。
ありがとうございます
こんにちは。高校入試でこのような問題は出ますか?
いや、こういったのは出ないんじゃないかな!