今回の記事では数学Ⅰで学習する三角比の単元から
「2直線のなす角、\(x\)軸の正の向きとなす角とは」
についてサクッと解説しておきます。
難しく思える問題ではあるのですが、やり方を知ったら誰でも簡単に解けるようになりますよ(^^)
ポイントは以下の通りです。
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
\(x\)軸の正の向きとのなす角とは
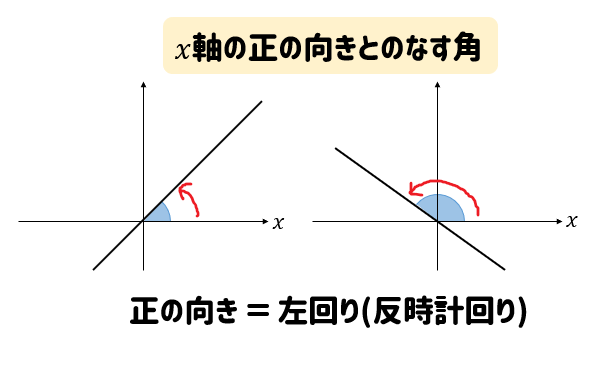
上のポイントでも述べていますが、\(x\)軸の正の向きとのなす角とは
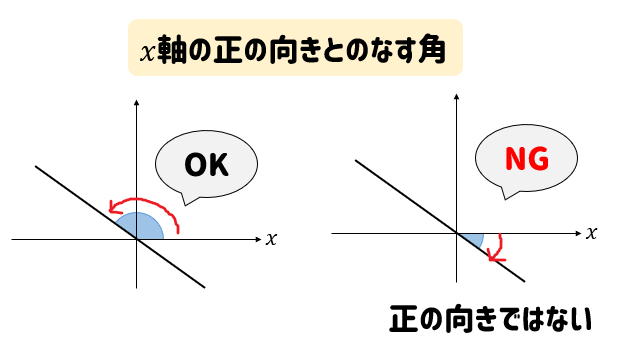
\(x\)軸から左回りにとった角のことをいいます。
見るべき角を間違えないようにしましょうね。
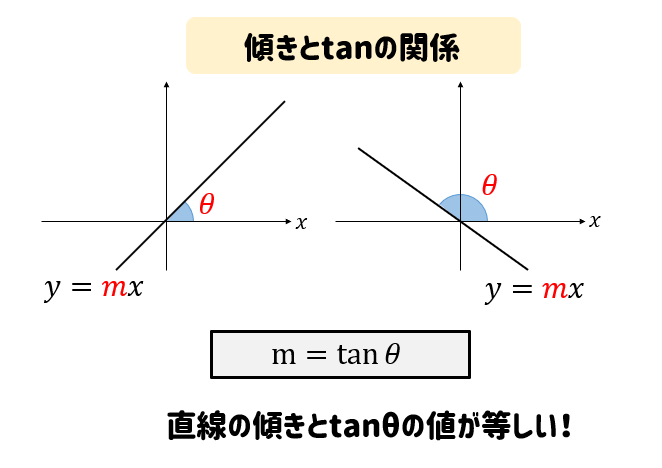
そして、この\(x\)軸の正の向きとの角を\(\theta\)として、\(\tan\theta\)の値を考えると、直線の傾きと等しくなるという特徴があります。

この性質を用いると、直線が\(x\)軸とどれくらいのなす角をしているのかを求めることができます。
【例題】
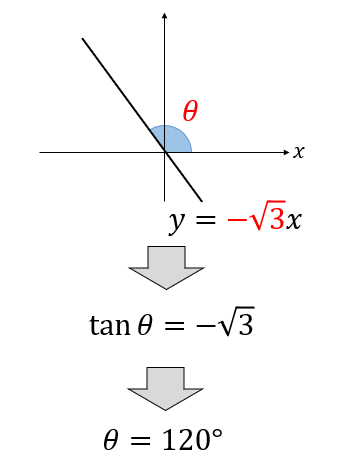
直線\(y=-\sqrt{3}x\)と\(x\)軸の正の向きとのなす角を求めなさい。
なす角を\(\theta\)とすると、直線の傾きは\(-\sqrt{3}\)なので
$$\tan\theta=-\sqrt{3}$$
と表すことができます。
\(\tan\)が何度のときに\(-\sqrt{3}\)になるのかっていうのは覚えておかなければなりませんが、ここから\(\theta=120°\)ということが読み取れます。
2直線のなす角の求め方
【問題】
2直線\(y=-x\)と\(y=\frac{1}{\sqrt{3}}x\)のなす鋭角を求めなさい。
2直線のなす角を求める場合には、上の章で紹介した\(x\)軸の正の向きとのなす角が役に立ちます。
まず、それぞれの直線の\(x\)軸の正の向きとのなす角を\(α,β\)とすると
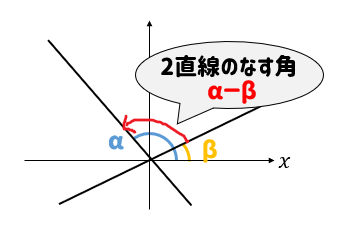
2直線のなす角は\(α-β\)で表すことができますね。
αとβの大きさをそれぞれ求めると
$$\begin{eqnarray}\tanα&=&-1\\[5pt]α&=&135° \end{eqnarray}$$
$$\begin{eqnarray}\tanβ&=&\frac{1}{\sqrt{3}}\\[5pt]β&=&30° \end{eqnarray}$$
このように求まりました。
よって、\(α-β=135-30=105°\)となります。
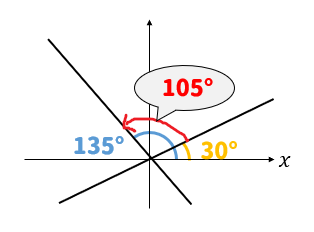
しかし!
求まった角度は105°、鈍角です。
問題では、なす鋭角を求めろと言われています。
鋭角というのは90°よりも小さい角のことです。
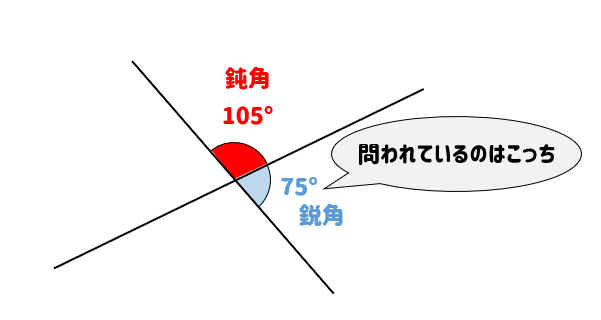
なので、答えとしては75°を解とします。
2直線のなす角には、鋭角と鈍角のものがあるのですが(直角の場合もあり)
問われているものに対して、最後に調整を加えるようにしてください。
切片がある場合にはどうする?
【問題】
2直線\(y=-\sqrt{3}x\)と\(y=x+2\)のなす鋭角を求めなさい。
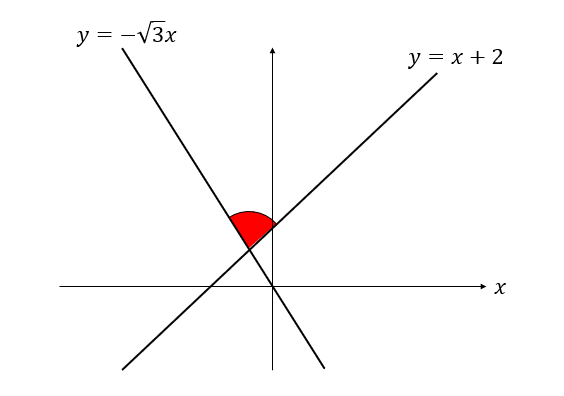
グラフにして考えると、上のような場所になります。
んーーーー
中途半端な場所で分かりにくい!!
ですが、ちょっと発想を変えてみると簡単に解けます。
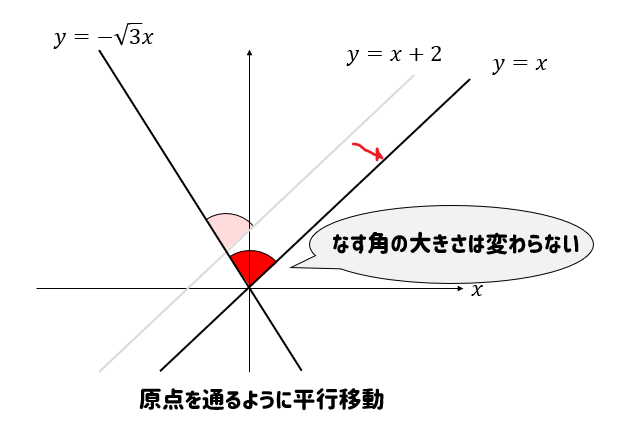
このように、\(y=x+2\)のグラフが原点を通るように平行移動してみましょう。
切片を無視して\(y=x\)のグラフにしちゃうってことだね。
これでも2直線のなす角は変わっていないことに気づくはずです。
つまり、2直線\(y=-\sqrt{3}x\)と\(y=x+2\)のなす角というのは
2直線\(y=-\sqrt{3}x\)と\(y=x\)のなす角を求めればOKってことになるね。
こうやって考えれば、上でやってきた問題と同じことだ!
2直線の\(x\)軸の正の向きとのなす角をそれぞれ\(α、β\)とすると
$$\begin{eqnarray}\tanα&=&-\sqrt{3}\\[5pt]α&=&120° \end{eqnarray}$$
$$\begin{eqnarray}\tanβ&=&1\\[5pt]β&=&45° \end{eqnarray}$$
よって、\(α-β=75°\)となりました。
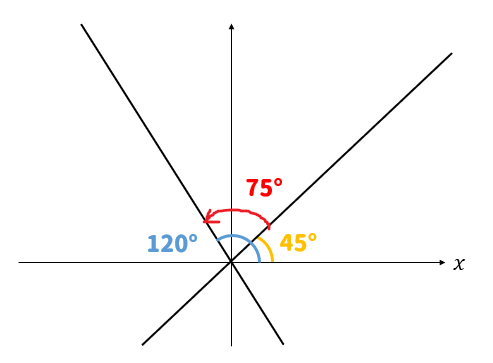
以上より、2直線のなす鋭角は75°となりました。
原点を通らない場合でも、平行移動して考えればよい。
切片は無視してしまおう!ってことだね(^^)
2直線\(y=ax+b\)と\(y=cx+d\)のなす角は
2直線\(y=ax\)と\(y=cx\)のなす角を考えればOK!
まとめ!
なす角を求めろ!
と言われると難しく感じてしまいますが単純な問題でしたね。
正の向きとのなす角がどこを表すのか。
tanの値と傾きが等しくなること。
この2点をしっかりと覚えておきましょう(^^)



















コメントを残す