二次不等式の解き方を簡単に！高校数学をマスターしよう！

今回は高校数学Ⅰで学習する

「二次不等式の解き方」

について解説していきます！

 

二次不等式には、たくさんのパターンが存在します。

それらの問題について丁寧に解説をつけているので、この記事を通して二次不等式は簡単だ！と感じてもらえると嬉しいです(^^)

 

今回の内容はこちらの動画でも解説しています！

二次不等式　グラフを使った解き方

二次不等式の解き方は以下の手順です。

それでは、例題を用いて解き方を確認してみましょう。

 

まず、\(x^2-6x+8=0\)を解きます。

$$x^2-6x+8=0$$

$$(x-4)(x-2)=0$$

$$x=2,4$$

すると、\(y=x^2-6x+8\)のグラフは

このような形になりますね。

問題では、このグラフが\(<0\)になる範囲を求めなさいということだから

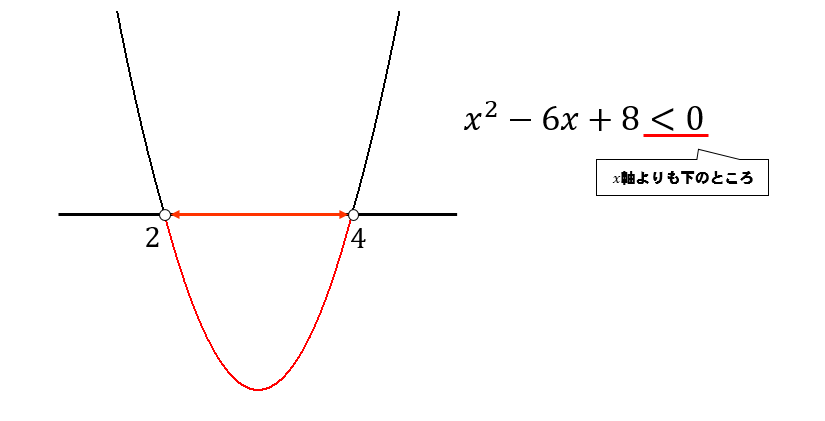
ここの部分の範囲を求めれば良いということになります。

よって、この二次不等式の解は

$$2<x<4$$

となります。

 

二次不等式を解くためには、このようにグラフを利用すると楽にできます(^^)

それでは、次の問題も見ておきましょう。

まず、\(x^2-6x+5=0\)を解きます。

$$x^2-6x+5=0$$

$$(x-5)(x-1)=0$$

$$x=1,5$$

\(y=x^2-6x+5\)をグラフにすると

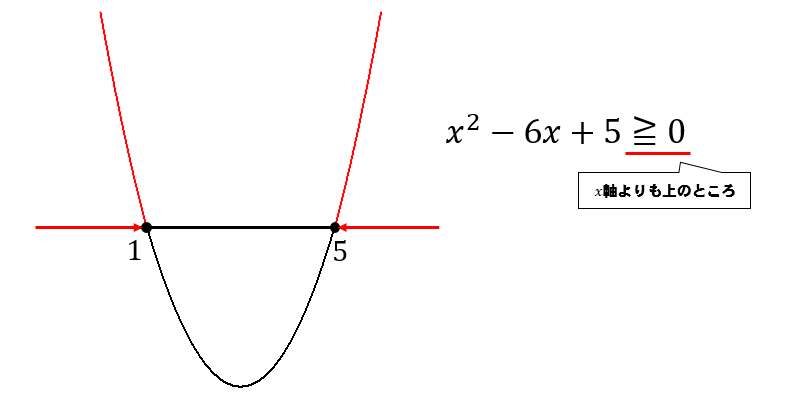
このようになるので、二次不等式の解は

$$x≦1 ,  5≦x$$

となります。

 

解の公式を用いるパターン

\(2x^2-x-4=0\)を解きたいのですが、因数分解ができませんね…(^^;

そういう場合には、解の公式を用います。

$$x=\frac{-(-1)\pm \sqrt{(-1)^2-4\times 2\times (-4)}}{2\times 2}$$

$$=\frac{1\pm \sqrt{33}}{4}$$

すこし複雑な値にはなってしまいますが、グラフは次のようになります。

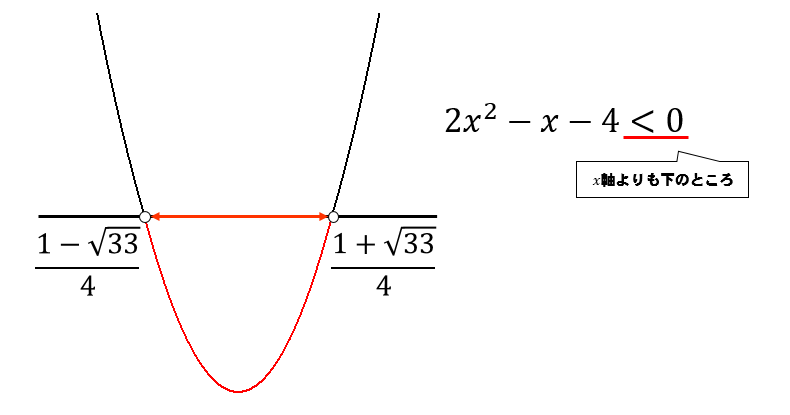
よって、二次不等式の解は

$$\frac{1-\sqrt{33}}{4}<x<\frac{1+\sqrt{33}}{4}$$

となります。

 

二次方程式を解くときに、因数分解ができないようであれば解の公式を利用するようにしましょう。

ちょっと複雑な値が出てくることもありますが、そこは自信を持って計算を進めるべし！

 

分数を含む二次不等式

このように不等式に分数を含む場合であっても、特別なことはありません。

分母にある２を両辺に掛けて、分数の形を消してやりましょう。

$$\frac{3}{2}x^2\times 2+\frac{5}{2}x\times 2-1\times 2>0$$

$$3x^2+5x-2>0$$

こうやって、分数が消えた形に変形してから二次不等式を解いていけばOKです。

 

$$3x^2+5x-2=0$$

$$(3x-1)(x+2)=0$$

$$x=-2,   \frac{1}{3}$$

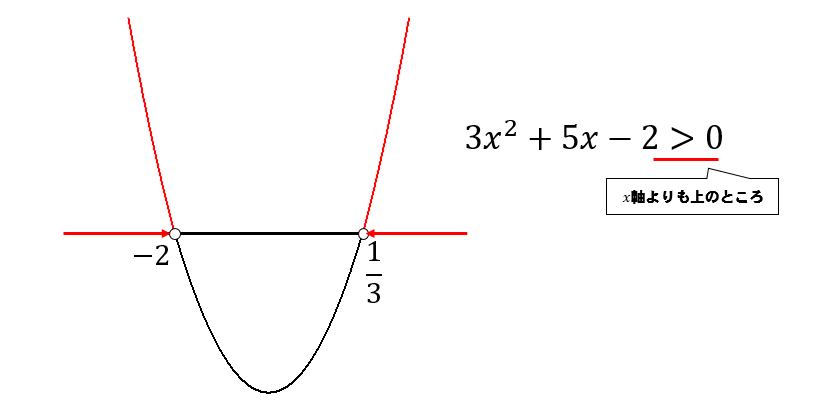
よって、二次不等式の解は

$$x<-2,  \frac{1}{3}<x$$

 

マイナスの二次不等式

このように二乗の係数がマイナスの場合

両辺に\((-1)\)を掛ける！

$$x^2-x-12≦0$$

このとき、不等号の向きを逆にすることも忘れないようにね！

 

こうすることによって、見た目が簡単になりました。

$$x^2-x-12≦0$$

あとは、この二次不等式を解いていけば良いです。

$$x^2-x-12=0$$

$$(x-4)(x+3)=0$$

$$x=-3,  4$$

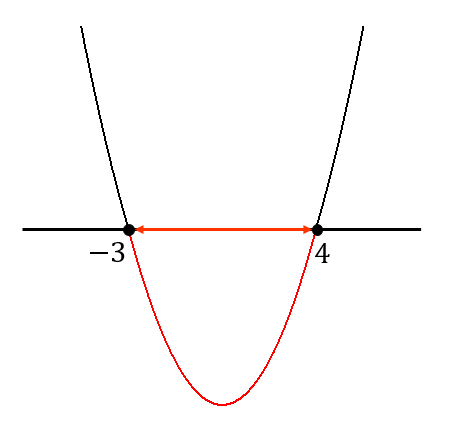
よって、この二次不等式の解は

$$-3≦x≦4$$

となります。

 

グラフが接するときの解き方

この不等式を解いていくと…

$$x^2+8x+16=0$$

$$(x+4)^2=0$$

$$x=-4$$

このように、二次方程式の解が１つ（重解）となってしまいます。

よって、グラフはこのようになります。

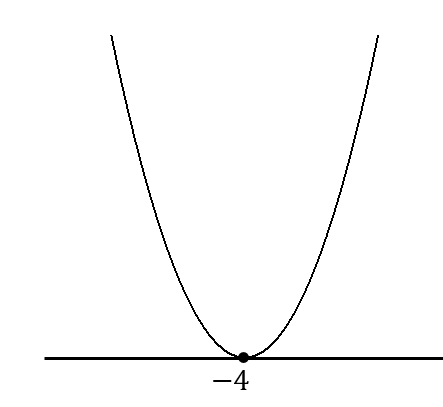
今までとは見た目がちょっと違いますね。

だけど、考え方は同じです。

\(>0\)となる範囲を求めたいので…

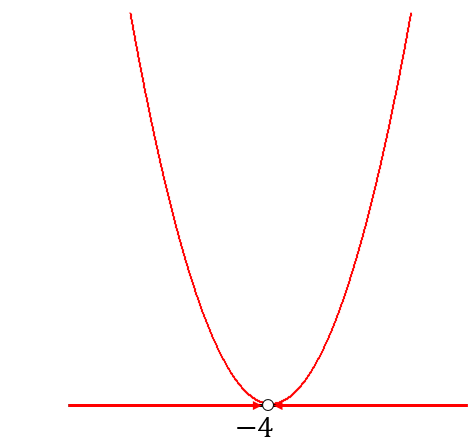
頂点以外のところは全部OKということになります。

\(>0\)だから、\(x\)軸上の場所はダメだからね！

 

よって、二次不等式の解は

\(-4\)以外のすべての実数

ということになります。

 

グラフが接するパターンの問題を他にも見ておきましょう。

$$x^2-10x+25=0$$

$$(x-5)^2=0$$

$$x=5$$

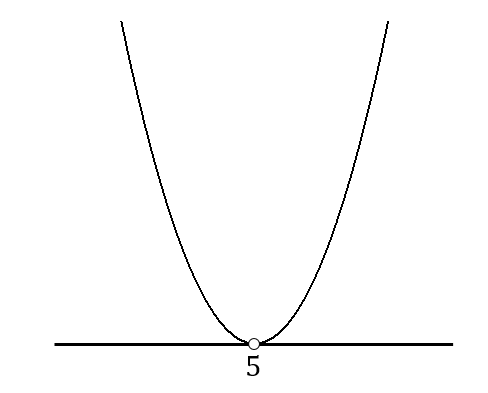
グラフが書けたら、\(<0\)となっている部分を見つけます。

しかし、このグラフにおいて\(<0\)となっている部分はありません。

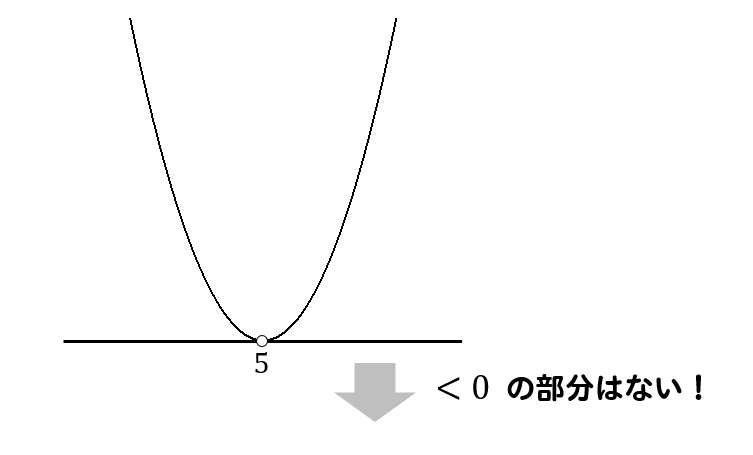
こういう場合には、二次不等式は

解なし

というのが求める解になります。

 

$$4x^2+4x+1=0$$

$$(2x+1)^2=0$$

$$x=-\frac{1}{2}$$

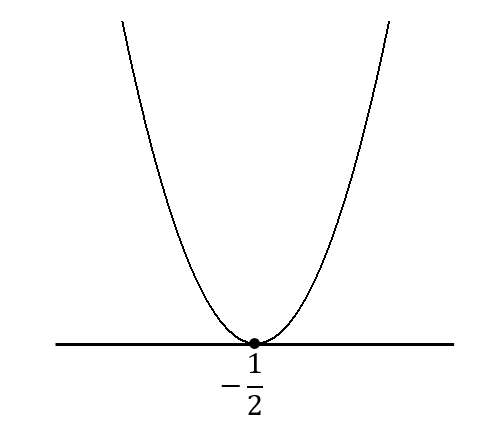
このグラフにおいて\(≧0\)になっている部分を見つけます。

すると…

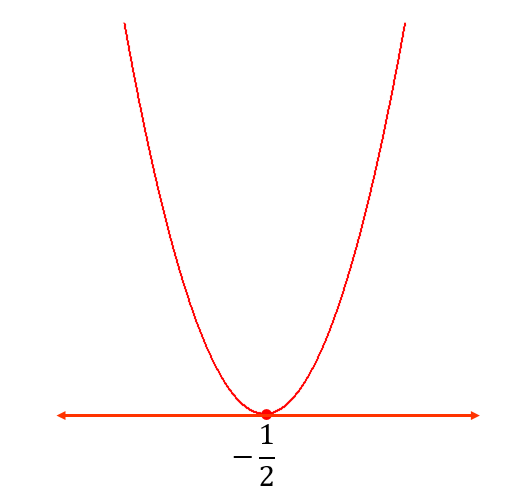
全部OKじゃん！！

ということに気が付くはずです。

\(≧0\)ということだから、\(x\)軸上の点もOKだよ。

 

よって、この二次不等式の解は

すべての実数

ということになります。

 

$$x^2+14x+49=0$$

$$(x+7)^2=0$$

$$x=-7$$

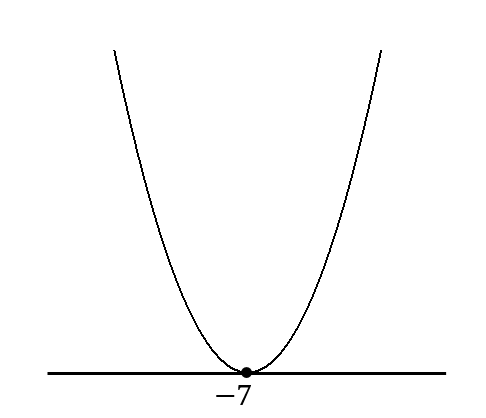
このグラフにおいて、\(≦0\)となる部分を見つけます。

すると…

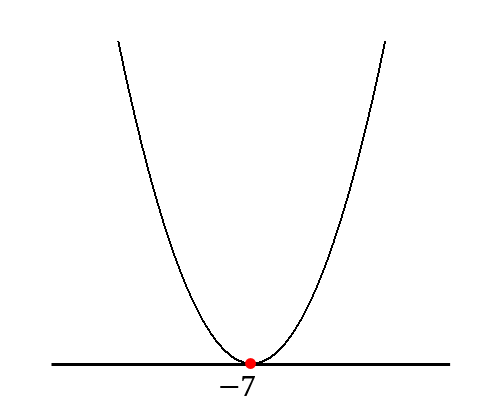
すると、\(x\)軸上にある\(-7\)だけOKということが分かります。

よって、この二次不等式の解は

$$x=-7$$

となります。

 

 

このようにグラフが接してしまう場合の解は、答え方の種類が様々です。

必ずグラフを書いて、範囲を確かめていきましょう。

共有点を持たない二次不等式

今までと同じ手順で不等式を解いていきます。

$$x^2-2x+6=0$$

$$x=\frac{2\pm\sqrt{4-24}}{2}$$

$$=\frac{2\pm\sqrt{-20}}{2}$$

あれ、あれれ…

ルートの中身がマイナスになってしまって困りますね。

つまり、この二次不等式を解を持たないということになります。

 

解を持たないということはグラフは

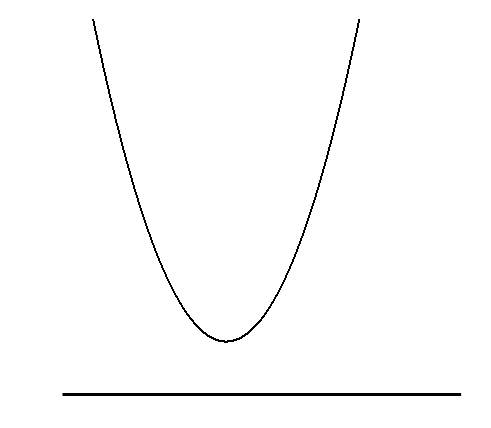
このように、\(x\)軸と共有点を持たず上に浮いたようなグラフになります。

 

グラフが\(x\)軸と共有点を持つかどうかは判別式を用いると簡単に分かります。

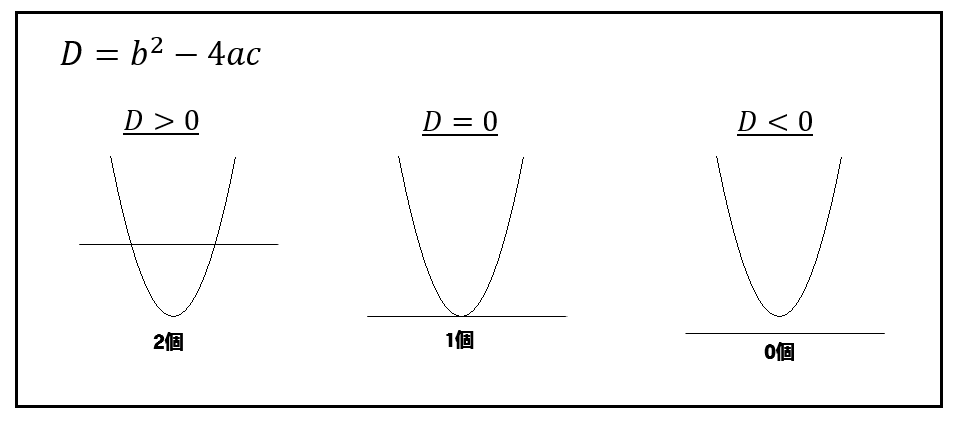
判別式の値が負になれば、\(x\)軸と共有点を持たないということが分かります。

 

以上のことを踏まえて、もう一度この二次不等式を解いていきます。

$$x^2-2x+6>0$$

$$D=(-2)^2-4\times 1\times 6$$

$$=4-24=-20<0$$

よって、グラフは次のようになります。

 

このグラフにおいて、\(>0\)になっている部分を見つけると

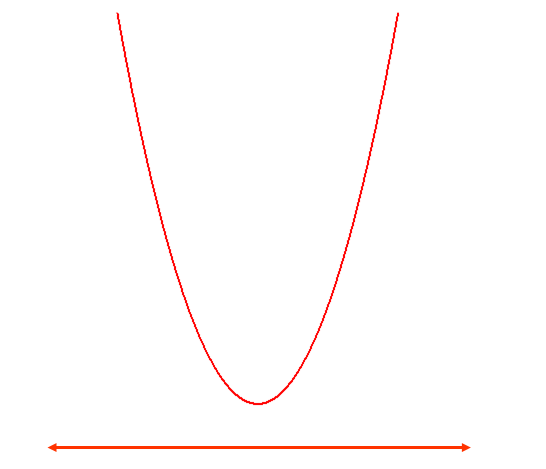
全部！ということになるので

この二次不等式の解は

すべての実数

ということになります。

 

今回の二次不等式のように、方程式が解けないぞ…

となれば、判別式を利用して共有点を持たないことを示しましょう。

そこから上に浮いているグラフを書いて範囲を求めていきます。

 

それでは、もう1問！

\(3x^2-8x+6=0\)の判別式をDとすると

$$D=(-8)^2-4\times 3\times 6$$

$$=64-72=-8<0$$

判別式が負となるので、グラフは次のような形になります。

このグラフにおいて、\(<0\)となる部分はないので

この二次不等式の解は

解なし

となります。

 

連立二次不等式の解き方

連立不等式を解く手順は

でしたね！

 

まず、それぞれの不等式を解いていきましょう。

$$x^2-x-6<0$$

$$x^2-x-6=0$$

$$(x-3)(x+2)=0$$

$$x=-2,  3$$

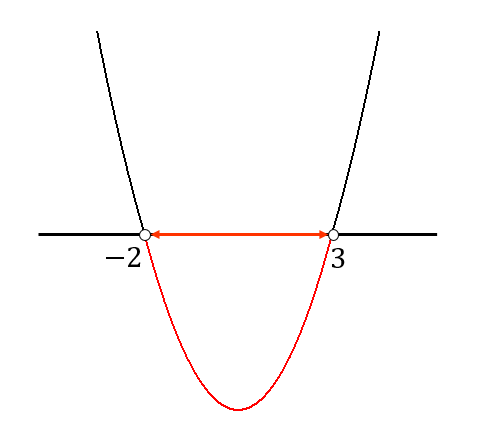
解は、\(-2<x<3\)　となります。

 

もう１つの不等式も解いていきましょう。

$$2x^2+3x-5≧0$$

$$2x^2+3x-5=0$$

$$(2x+5)(x-1)=0$$

$$x=-\frac{5}{2},  1$$

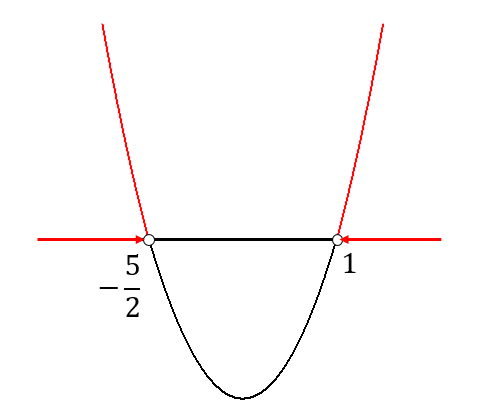
解は、\(\displaystyle{x≦-\frac{5}{2},  1≦x}\)　となります。

 

 

それぞれの不等式が解けたら共通範囲を求めていきましょう。

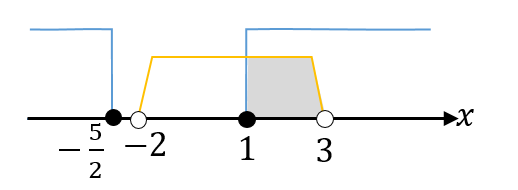
すると、共通範囲は

$$1≦x<3$$

ということが読み取れます。

これが連立不等式の解となります。

 

【応用】係数に文字を含む二次不等式

次は二次不等式の応用問題として、係数に文字を含むパターンについて解説していきます。

まずは、今までの二次不等式と同じように解いていきます。

$$x^2+(3-a)x-3a=0$$

$$(x+3)(x-a)=0$$

$$x=-3,  a$$

よっしゃ、方程式も解けたのでグラフを書くぞ！

あれ、あれれ…

ここで困ったことが発生してしまいます。

 

なぜなら…

\(-3\)と\(a\)、どちらが大きいか分からないからグラフが書けないのです！！

\(a\)の値次第では、次の3パターンのグラフが考えられます。

 

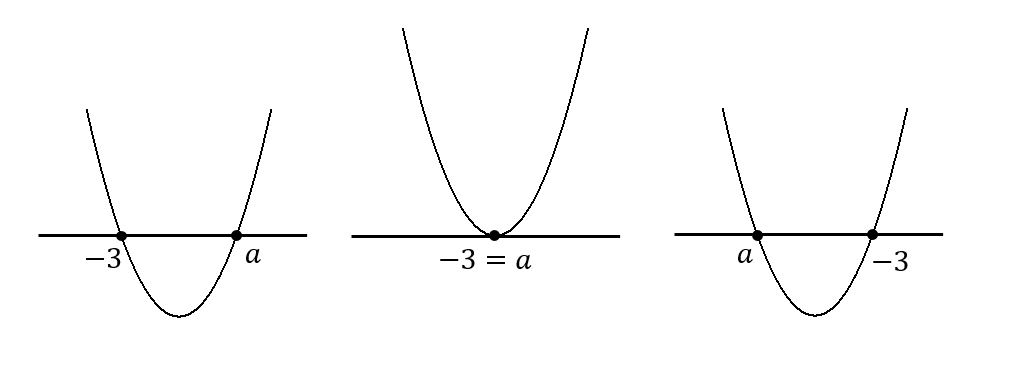
なので、場合分けをして考えていきます。

\(-3<a\)のとき、次のようなグラフになります。

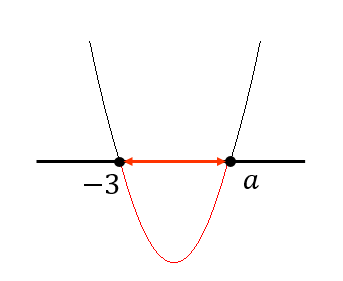
よって、\(-3<a\)のとき \(-3≦x≦a\)となります。

 

 

次に、\(a=-3\)のとき、次のようなグラフになります。

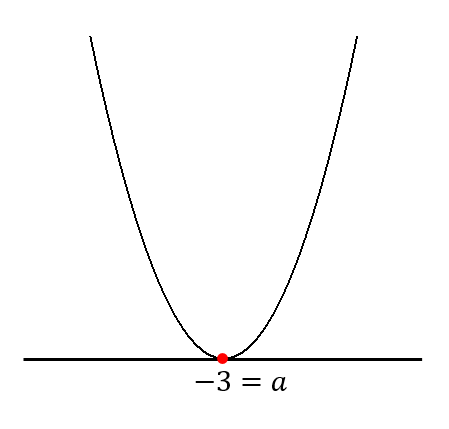
よって、\(a=-3\)のとき \(x=-3\)となります。

 

 

最後に、\(a<-3\)のとき、次のようなグラフになります。

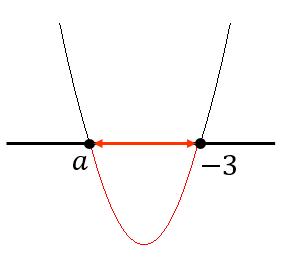
よって、\(a<-3\)のとき　\(a≦x≦-3\)となります。

 

 

これらをまとめると、この二次不等式の解は

\(-3<a\)のとき \(-3≦x≦a\)

\(a=-3\)のとき \(x=-3\)

\(a<-3\)のとき　\(a≦x≦-3\)

となります。

 

 

今回の二次不等式のように係数に文字を含む場合には、グラフが１つに決められずいくつかのパターンを考える必要があります。

そのため、考えられるパターンを書き出して場合分けをすることで解を求めていきましょう。

 

まとめ

お疲れ様でした！

正直…二次不等式は難しいね

だけど、高校数学のすっごい大事な単元でもあるから頑張って理解しておきたいね(^^)

 

解き方を理解したら、いろんな問題に挑戦して理解を深めていきましょう！

ファイトだ(/・ω・)/