今回は高校数学Ⅱで学習する
「対数関数」という単元から
logのグラフの書き方について解説していくよ!
logのグラフの基本的な特徴
平行移動を利用した発展系まで
徹底的に解説していくぞー!
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
logグラフの基本性質
logのグラフには2つの形があります。
それがコレ!
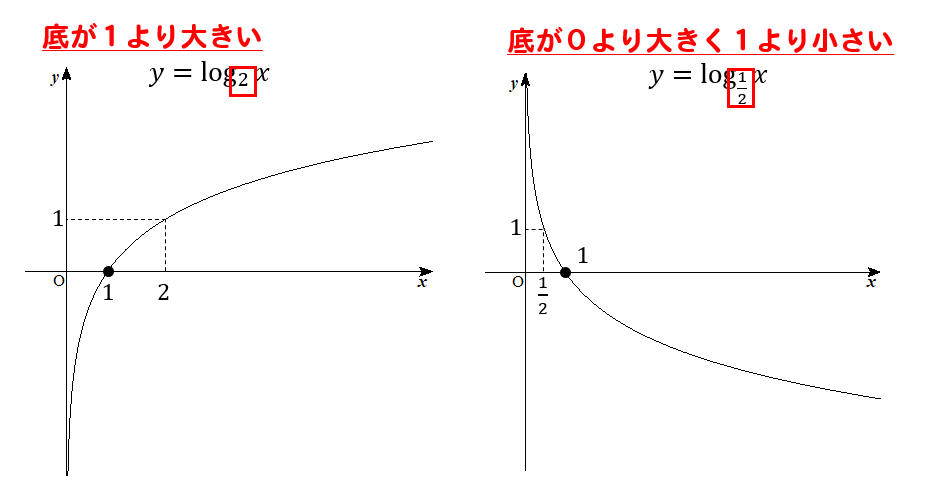
logについている小さい数、つまり底の数によってグラフの形が異なります。
底が1より大きい場合には、右に上がっていくグラフ
底が0より大きく1より小さい場合には、右に下がっていくグラフとなります。
そして、どちらのパターンにも共通している特徴があるのでまとめておきます。
- \((1,0)\)を通る。
- \(x\)座標が底と同じ値のとき、\(y\)座標は1になる。
- \(y\)軸が漸近線となる
\((1,0)\)を通る
logは、真数が1になると値が0になってしまいます。
これは底がどんな値でも関係ありませんね。
$$\log_{2}1=0$$
$$\log_{\frac{1}{2}}1=0$$
だから、logのグラフを書く場合には
まず、\((1,0)\)の点を書いてやりましょう。
\(x\)座標が底と同じ値のとき、\(y\)座標は1になる。
logの特徴から、\(x\)の値が底と同じ値のとき、\(y\)座標は1になります。
$$\log_{2}2=1$$
$$\log_{\frac{1}{2}}\frac{1}{2}=1$$
よって、グラフを書くときには
\((底の値, 1)\)となる座標をとってやりましょう。
\(y\)軸が漸近線となる
漸近線とは、決して交わることのない線のことをいいます。
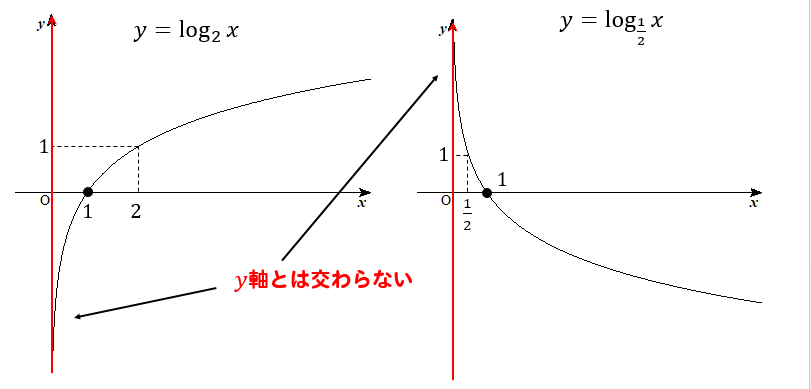
logのグラフでは、\(y\)軸が漸近線となっており
グラフをどこまで伸ばしていっても決して\(y\)軸と交わることはありません。
logグラフの書き方
それでは以上の基本性質をおさえた上で、logグラフの書き方についてみていきましょう。
手順は以下の通りです。
- \((1,0)\)の点を取る
- \((底の値, 1)\)の点を取る
- 底の値からグラフの形を読み取り、①②の点を結ぶ
それでは、\(y=\log_{3}x\)のグラフを手順通りに書いてみましょう。
手順① \((1,0)\)の点を取る
まずは\((1,0)\)のところに点を取りましょう。
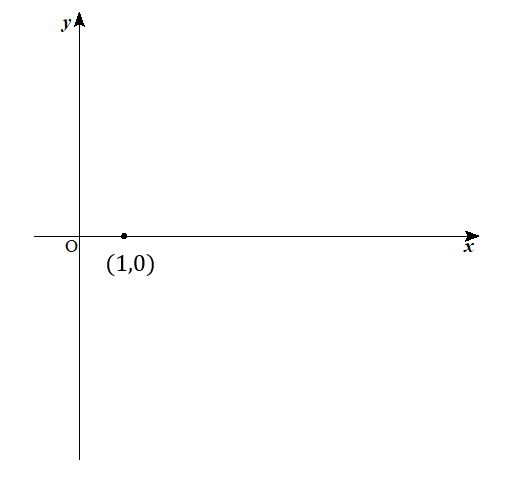
手順② \((底の値, 1)\)の点を取る
\(y=\log_{3}x\)のグラフは底が3であるから
\((3,1)\)の点を取りましょう。
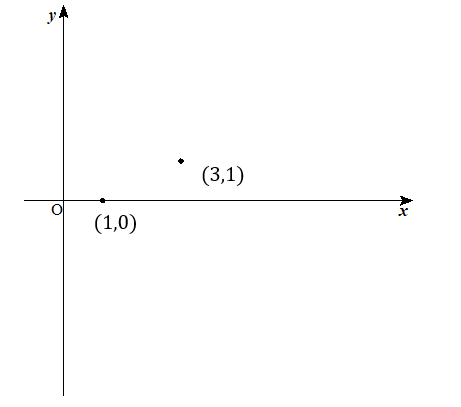
手順③ 底の値からグラフの形を読み取り、①②の点を結ぶ
底が3なので、右に上がっていくグラフだということが分かります。
よって、2点を通っていて右に上がっていくようにグラフを書いていきましょう。
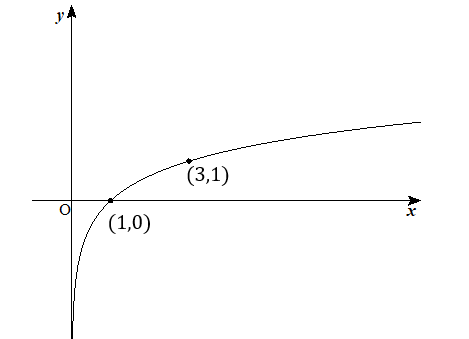
これで完成です!
このとき、グラフが\(y\)軸とはぶつからないように気を付けてくださいね。
logのグラフ簡単でしたね
たったの3ステップで書いてやることができました(^^)
それでは、logグラフの基本編をマスターした方は、平行移動を利用した発展バージョンもやっておきましょう。
平行移動を用いたグラフの書き方
次の関数のグラフを書きなさい。
$$y=\log_{2}(x-2)$$

ということで、まずは\(y=\log_{2}x\)のグラフを書きます。
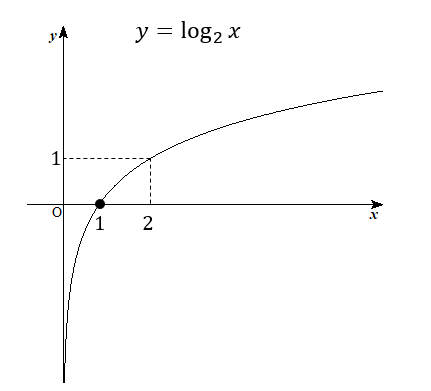
そして、このグラフを\(x\)軸方向に2ずつずらしてやります。
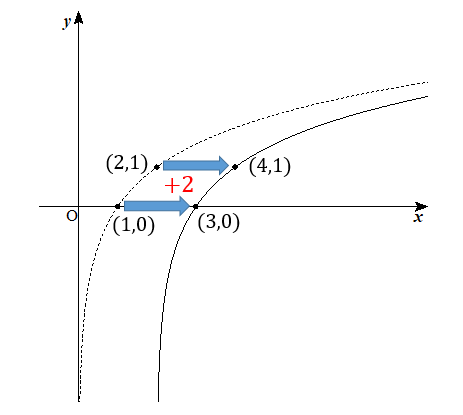
これで完成となります!
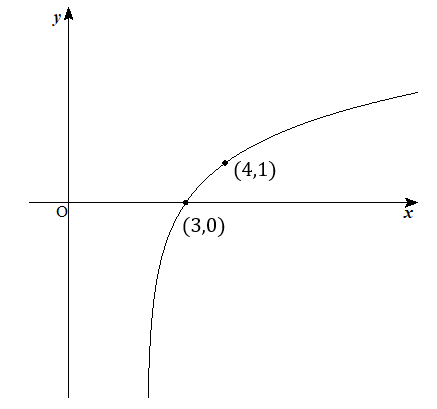
次の関数のグラフを書きなさい。
$$y=\log_{\frac{1}{2}}2x$$
これは一見、平行移動と関係がないように見えるのですが、式を変形すると次のようになります。
$$y=\log_{\frac{1}{2}}2x$$
$$=\log_{\frac{1}{2}}x+\log_{\frac{1}{2}}2$$
$$=\log_{\frac{1}{2}}x-1$$
つまり、このグラフは…

まずは、\(y=\log_{\frac{1}{2}}x\)のグラフを書いて\(y\)軸方向へ\(-1\)ずらしていきましょう。
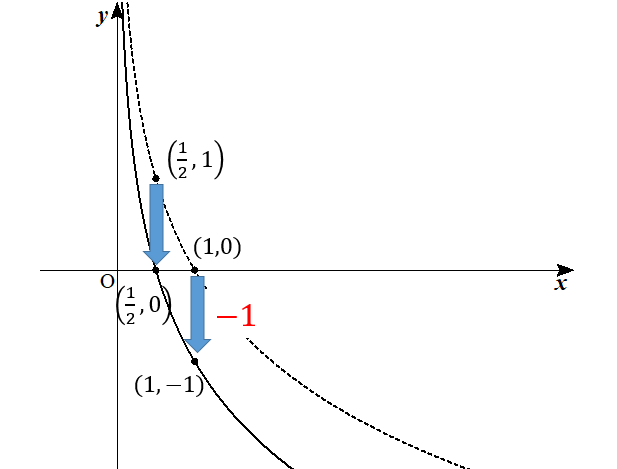
これで完成となります。
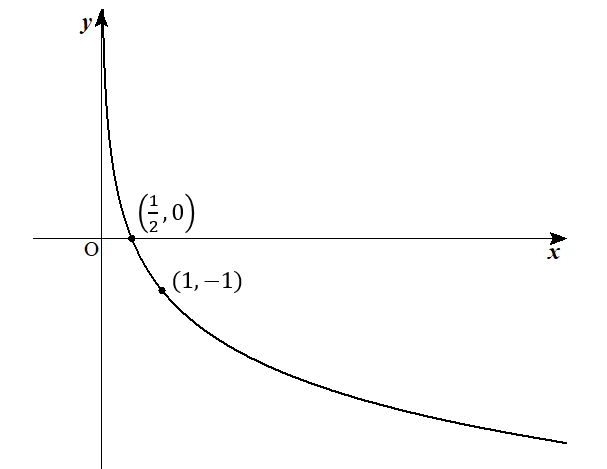
マイナスのlogグラフ
次の関数のグラフをかきなさい。
$$y=-\log_{2}x$$

つまり、\(y=\log_{2}x\)のグラフを\(x\)軸で折り返していけばグラフが完成します。
よって
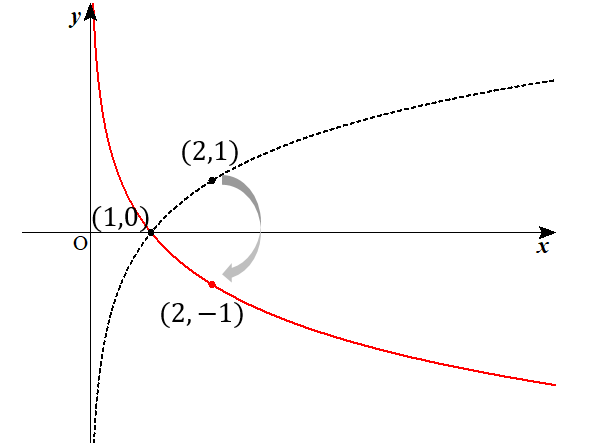
このようにグラフが完成します。
logにマイナスがついてるのだから、\(y\)座標の符号がひっくり返る。
なんとなくイメージはできるかな。
次の関数のグラフをかきなさい。
$$y=\log_{2}(-x)$$

だから、こんなグラフになります。
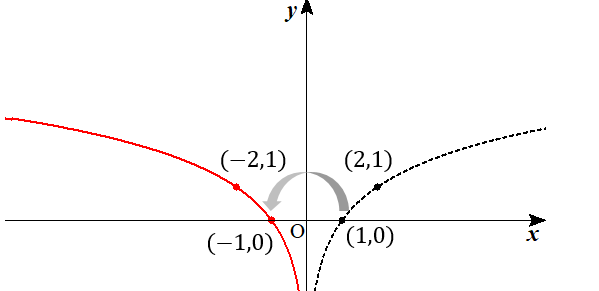
まとめ
お疲れ様でした!
logグラフの基本をおさえておけば、応用も大丈夫!
元のグラフの形が分かれば、そこから平行移動、対称移動もバッチリのはずです。
グラフの手順が分かれば、あとは練習あるのみです。
ファイトだ(/・ω・)/
















コメントを残す