重複順列の基本問題の解き方をイチから解説するぞ！

今回は高校数学Aで学習する場合の数の単元から「重複順列の基本問題」について解説します。

重複順列とは…

かっこよく説明するとこんな感じなんだけど…

こんな堅苦しい説明では、ぶっちゃけよくわからないよね(^^;)

 

なので、今回は以下の基本問題を使って重複順列について解説していくよ！

では、それぞれの解き方を解説していくぞー！

 

今回の内容はこちらの動画でも解説しています(^^)v

（1）5人がじゃんけんするときの手の出し方

5人がじゃんけんをするとき、1人目の手の出し方は何通りありますか？？

「グー、チョキ、パー」の3通りですよね。

 

では、2人目の手の出し方は？

もちろん「グー、チョキ、パー」の3通りです。

3人目、4人目、5人目、みーんな3通りの手の出し方があります。

 

このように、それぞれの選択肢が減っていかないような順列のことを重複順列といいます。

簡単にいいかえると「何度でも繰り返しOKの順列」のことです。

 

今回の問題では、みーんな3通りの手の出し方があるので

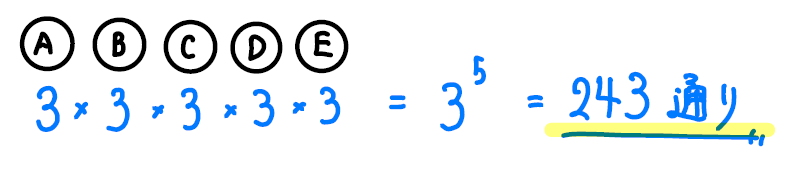
このように3を5回分かけてやれば手の出し方の総数が求まります。

簡単ですね！

 

同じように考えてみると次の場合も簡単に求まります。

（2）1,2,3,4で重複OKの3桁整数

3桁の整数をつくるので、百の位、十の位、一の位を表す3マスの表をつくります。

そのマスの中に何通りの数を入れることができるか考えていきましょう。

 

すると、百の位には「1～4」の4通り。

くり返しOKなので、十の位も「1～4」の4通り。

同じく、一の位も「1～4」の4通り。

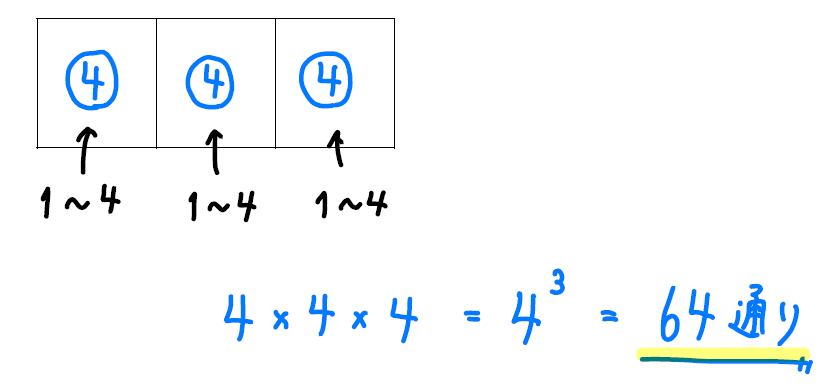
めっちゃ簡単ですね！

「重複を許して」という問題文を絶対に見落とさないようにね！

（3）0,1,2,3で重複OKの3桁整数

さっきと同じく3マスの表を使うのですが、ちょっとだけ注意！

今回の数字には「０」が含まれています。

0は百の位に置くことができないので

（百の位に0をおくと3桁じゃなくなるから）

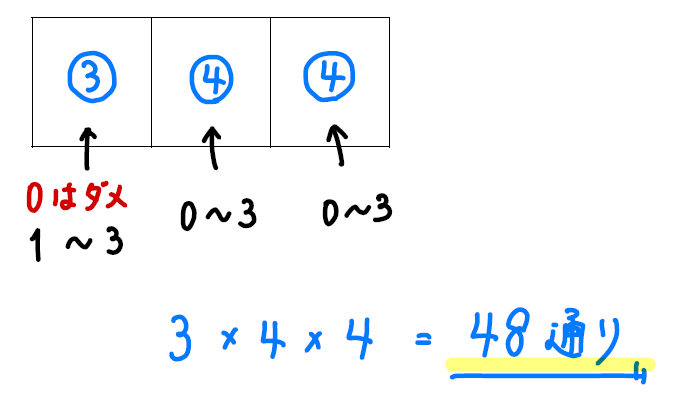
このように百の位のところだけは3通りにして計算していきましょう！

 

まとめ

お疲れ様でした！

重複順列の意味がなんとなーく伝わりましたか？？

くり返しOKだから、同じ数を何回もかけていくってことですね！

意味が分かってしまえばめちゃくちゃ簡単な問題なのでテストの得点源にしちゃってください＾＾

 

さて、重複順列の基本をマスターした方は、

「もうちょっと難しいのもやりたいなぁー」

と、物足りなさを感じている頃だと思う。

 

そこで！

重複順列の応用演習も用意しました(‘ω’)ノ

あ、こんな風にも使えるのか…と新しい発見があるはずです！

⇒　3分でバッチリ！部分集合の個数の求め方についてイチから解説するぞ！

⇒　【場合の数】部屋割りの考え方についてイチから解説！