【場合の数】部屋割りの考え方についてイチから解説！

高校数学Aで学習する場合の数の単元から

「部屋割りの場合の数」

についてサクッと解説してきます。

取り上げる問題はこちら！

今回の問題はこちらの動画でも解説しています。

サクッと理解したい方は動画がおススメです＾＾

部屋割り問題①の解説！

5人それぞれには、部屋A，Bのどちらかに入るという2通りのパターンがあります。

よって、2通りが5人分ってことで、\(2^5=32\)通りと計算することができます。

（1）で求めた場合の数の中には、

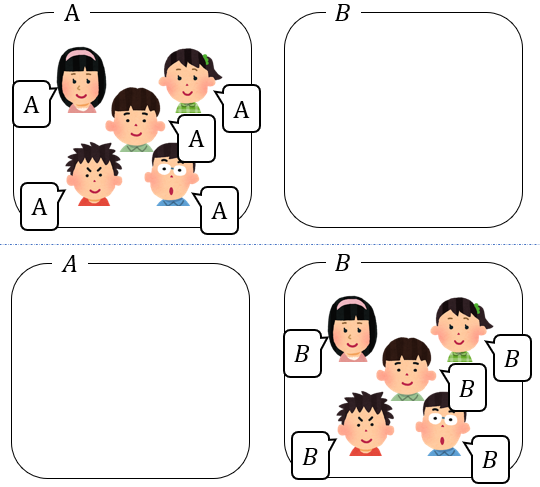
このように全員がAだけに入り、Bが空室になるパターン。

全員がBだけに入り、Aが空室になるパターンが含まれています。

よって、空室がない場合は全体からこの2通りを引けばいいので、\(32-2=30\)通りとなります。

空室ありのパターンは簡単に求めることができます。

しかし、その中には全員が同じ部屋に入ってしまい、空室ができるパターンも含まれているってことを覚えておいてくださいね。

部屋割り問題②の解説！

では、3つの部屋で空室がないパターンを考えてみましょう。

まずは、「空室あり」も含めた全体の場合の数を求めてみましょう。

すると、3通りが4人だから \(3^4=81\)となります。

ここから空室がでてしまうパターンを引いていきましょう。

部屋が3つあるときには、次のような空室パターンが考えられます。

【空室が2つになるパターン】

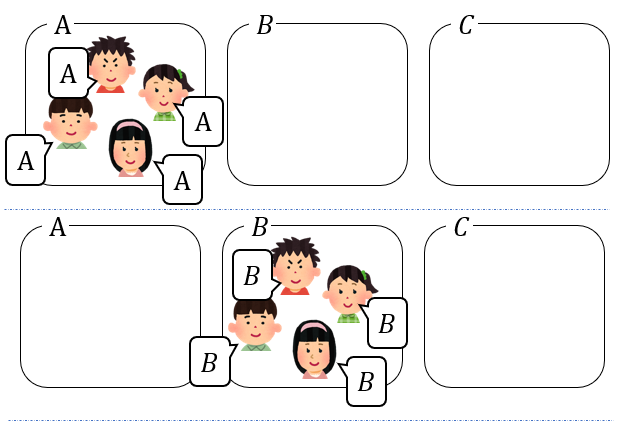
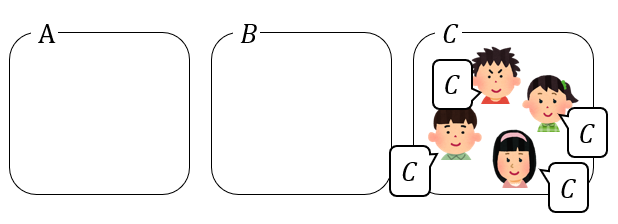
全員が同じ部屋に入り、空室が2つになるのが3通り。

【空室が1つになるパターン】

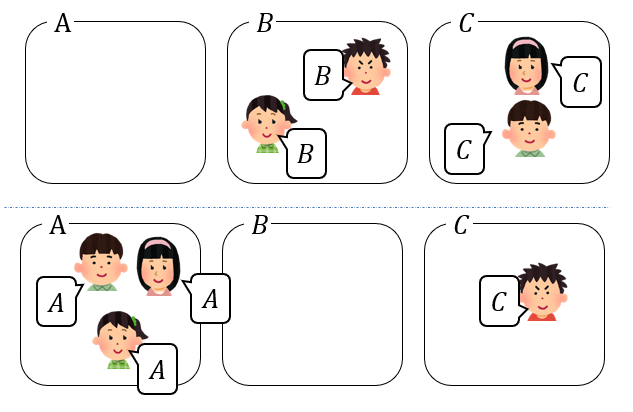
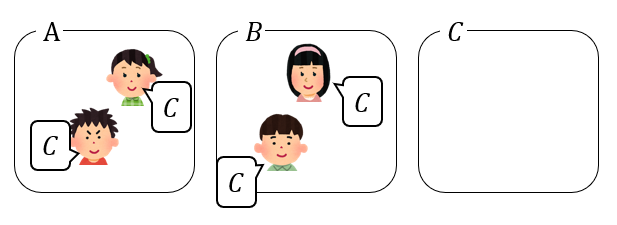
A，B，Cがそれぞれ空室になる3通り考えることができます。

例えば、Aのみが空室になる場合の部屋の入り方が何通りあるか考えてみましょう。

全員がB，Cのどちらかの部屋に入ることになるので、\(2^4=16\)通り。

ただ、この中には全員がBに入る、Cに入るパターンも含まれており、これを取り除く必要があります。

よって、\(16-2=14\)通りとなります。

同様に、Bのみが空室になる場合も14通り。

Cのみが空室になる場合も14通りになります。

以上より、全体から空室になる場合を引けばいいので

\(81-(3+14\times 3)=81-45=36\)通りとなります。

部屋が3つになると、空室になるパターンが複雑になります。

パターンを書き出してみて、ていねいに考えていくのが大事ですね。

まとめ！

お疲れ様でした！

空室ありの場合は簡単ですね。

\((選択肢の数)^{人数}\) で求めることができます。

ですが、この数の中には空室がでるパターンも含まれているので、

空室なしを考える場合には、全体から空室パターンを取り除く必要があります。

たくさん問題を解いて、パターン分けがスムーズにできるよう練習しておきましょう！