同じものを含む順列では、次のように場合の数を求めます。
\(a,a,a,b,b,c\) の6個の文字を1列に並べるとき,並べ方は何通りあるか。
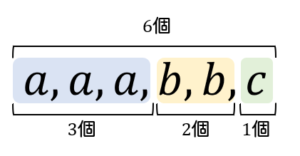
$$\begin{eqnarray}\frac{6!}{3!2!1!}=60通り \end{eqnarray}$$

なぜ同じものの個数の階乗で割るのでしょうか?
また、この公式は組み合わせCを使って表すこともできます。
この記事を通して、「公式のなぜ」について理解を深めておきましょう。
また、記事の後半には公式を利用した問題の解き方についても解説しているので、ぜひご参考ください!
なぜ?同じ順列を含む公式
なぜ同じものの個数の階乗で割らなければならないのでしょうか。
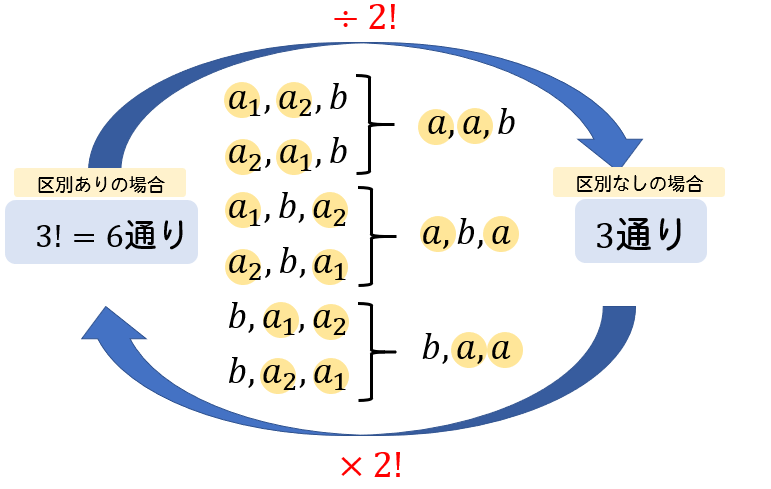
\(a,a,b\) の3個の文字を1列に並べるときを例に考えてみましょう。
同じ文字 \(a\) が2個あるわけなんですが、これがすべて違うものだとして並べかえを考えると、次のようになります。

3個の文字の並べかえなので、\(3!=6\)通りとなりますね。
しかし、実際には \(a\) は同じ文字になるので、3通りが正しい答えとなります。
ここで注目していただきたいのが、
区別なし ⇒ 区別ありにはどのような違いがあるかです。
区別なしの文字列に含まれている同じ文字を並べかえた分だけ、区別ありの場合の数は増えているはずです。
つまり、今回の例題では \(a\) が2個分あるので、\(\times 2!\) となっています。
次に、これを逆に考えてみると
区別あり ⇒ 区別なしのときには、\(\div2!\) されているってことになりますね。
よって、場合の数を求める計算式は次のようになります。
つまり、同じ文字を含む順列を考える場合のイメージとしては、
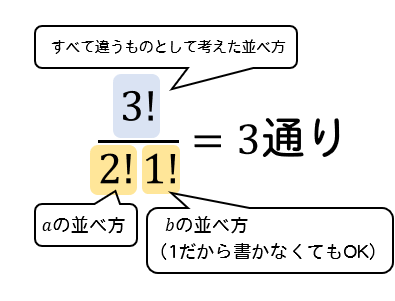
まずはすべてが違うものだとして、階乗で並べかえを考える。
次に、同じ文字として考え、同じ並びになっているものを省いていく。
その省き方が、同じ文字の個数の階乗で割ればよい。
という流れになります。
なぜ同じ文字の個数で割らなければならないの?
という疑問に対しては、
\(n!\) という計算では「区別あり」の場合の数しか求めることができません。
そのため、同じ文字の個数の階乗で割ることによって、ダブりを省く必要があるからです。
というのがお答えになりますね(^^)
ちょっと、難しいお話ではあるんだけどイメージは湧いたかな?(^^;)
んー、イマイチだなぁという方は、次の章でCを使った考え方と公式の導き方を説明しておきますので、ぜひご参考ください。
組み合わせCを使って考えることもできる
例題で取り上げた \(a,a,a,b,b,c\) の6個の文字を並べる場合の数は、次のようにCを使って計算することもできます。

発想はとても簡単なことです。
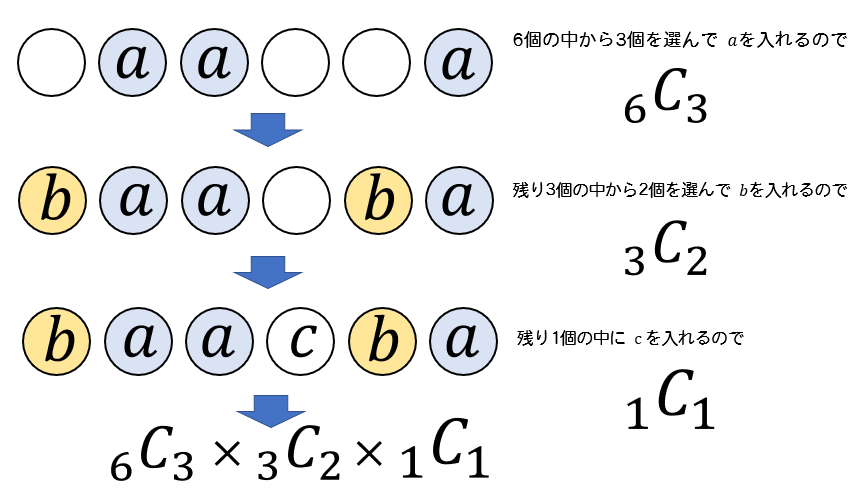
このように文字を並べる6つの枠を用意して、
\(a\)の文字をどこに入れるか ⇒ \(_{6}C_{3}\)
\(b\)の文字をどこに入れるか ⇒ \(_{3}C_{2}\)
\(c\)の文字をどこに入れるか ⇒ \(_{1}C_{1}\)
と、考えることができます。
文字に区別がないことから、このように組み合わせを用いて求めることができるんですね。
そして!
$$_{n}C_{r}=\frac{n!}{r!(n-r)!}$$
であることを用いると、
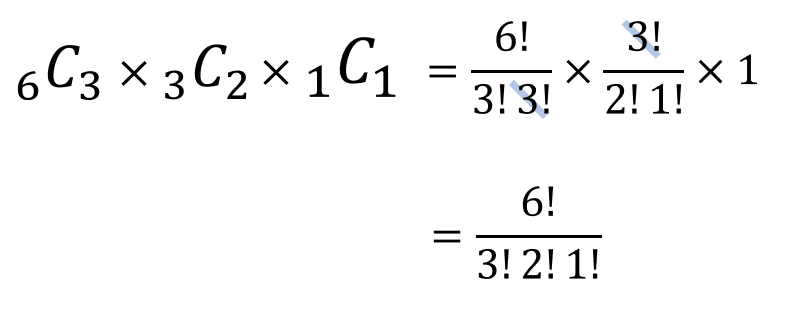
このように、階乗の公式を使った式と同じになることが確かめられます。
このことからも、なぜ同じ文字の個数の階乗で割るの?という疑問を解決することができますね(^^)
では、次の章では問題演習を通して、同じものを含む順列の理解を深めていきましょう。
同じものを含む順列の公式を用いた問題
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
同じものを含む順列【文字列】
【問題】
baseball の8文字を1列に並べるとき,異なる並べ方は何通りあるか。
まずは文字の個数を調べておきましょう。
a : 2文字 b : 2文字 e : 1文字 l : 2文字 s : 1文字 となります。
よって、
$$\begin{eqnarray}&&\frac{8!}{2!2!2!1!1!1!}\\[5pt]&=&\frac{8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{2\cdot 2\cdot 2}\\[5pt]&=&5040通り\cdots (解) \end{eqnarray}$$
答え
$$5040通り$$
同じものを含む数字を並べてできる整数(偶数)
【問題】
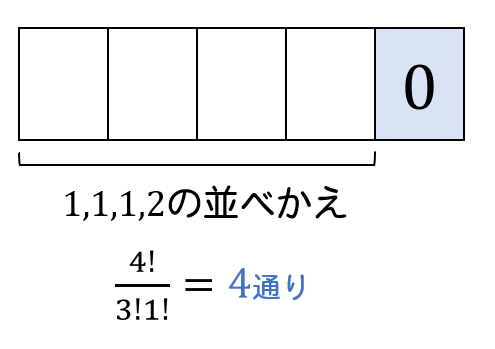
\(0,1,1,1,2\) の5個の数字を1列に並べて5桁の整数をつくるとき,偶数は何個できるか。
偶数になるためには、一の位が0,2のどちらかになります。
(一の位が0のとき)
(一の位が2のとき)
一の位が2のとき、残った数から一万の位を決めるわけですが、0を一万の位に入れることはできないので、自動的に1が入ることになります。
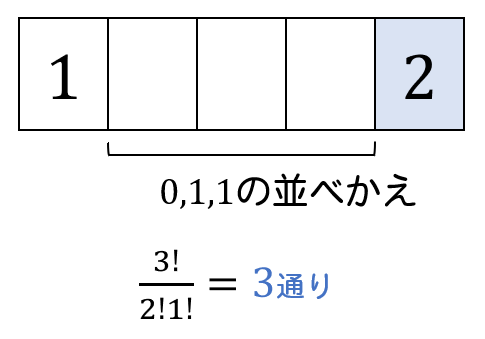
以上より、\(4+3=7\)通り。
答え
$$7通り$$
最短経路
【問題】
下の図のような道路がある。AからBへ最短の道順で行くとき,次のような道順は何通りあるか。
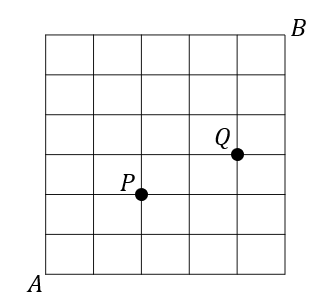
(1)総数
(2)PとQを通る
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
右に進むことを「→」
上に進むことを「↑」と表すことにすると、
AからBへの道順は「→ 5個」「↑ 6個」の並べかえの総数に等しくなります。
よって、AからBへの道順の総数は
$$\begin{eqnarray}\frac{11!}{5!6!}=462通り \end{eqnarray}$$
答え
$$(1) 462通り$$
PとQを通る場合には、
「A→P→Q→B」というように、道を細かく区切って求めていきましょう。
(A→Pへの道順)
「→ 2個」「↑ 2個」の並べかえだから、
$$\begin{eqnarray}\frac{4!}{2!2!}=6通り \end{eqnarray}$$
(P→Qへの道順)
「→ 2個」「↑ 1個」の並べかえだから、
$$\begin{eqnarray}\frac{3!}{2!1!}=3通り \end{eqnarray}$$
(Q→Bへの道順)
「→ 1個」「↑ 3個」の並べかえだから、
$$\begin{eqnarray}\frac{4!}{1!3!}=4通り \end{eqnarray}$$
「A→P」かつ「P→Q」かつ「Q→B」なので
\(6\times 3\times 4=72\)通りとなります。
答え
$$(2) 72通り$$
順序が指定された順列
【問題】
\(A, B, C, D, E\) の5文字を1列に並べるとき,次のような並べ方は何通りあるか。
(1)\(A, B, C\) の3文字がこの順になる。
(2)\(A\) が \(B\) より左に,\(C\) が \(D\) より左にある。
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
指定された文字を同じものに置き換えて並べる。
並べた後に、置き換えたものを左から順に\(A,B,C\)と戻していきましょう。
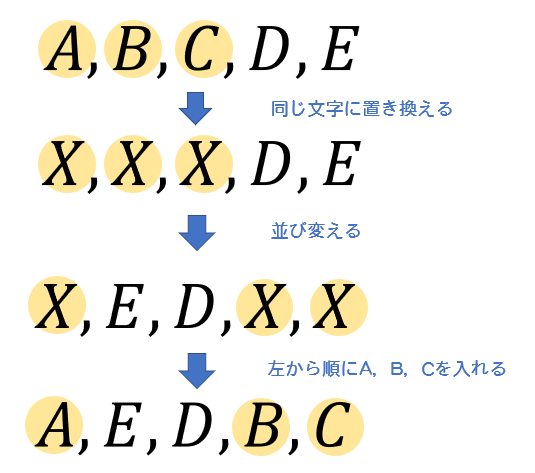
そうすれば、求めたい場合の数は「\(X,X,X,D,E\)」の順列によって計算することができます。
よって、
$$\begin{eqnarray}\frac{5!}{3!1!1!}=20通り \end{eqnarray}$$
答え
$$(1) 20通り$$
\(A\) が \(B\) より左に,\(C\) が \(D\) より左にある。
この問題では、「A,B」「C,D」をそれぞれ同じ文字に置き換えて考えていきましょう。
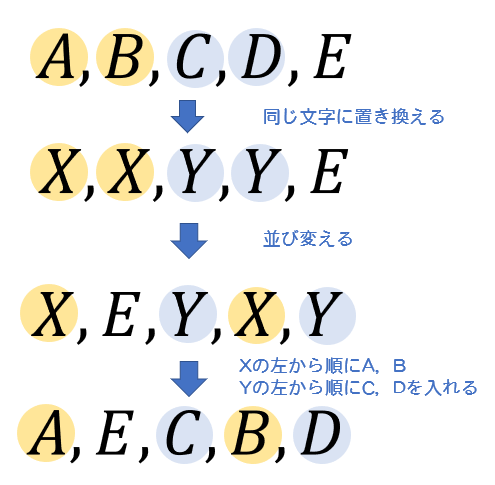
つまり、求めたい場合の数は「\(X,X,Y,Y,E\)」の順列によって計算することができます。
よって、
$$\begin{eqnarray}\frac{5!}{2!2!1!}=30通り \end{eqnarray}$$
答え
$$(2) 30通り$$
同じものを含むものから選ぶ順列
【問題】
\(a,a,a,b,b,c\) の6文字の中から,4文字を取り出して1列に並べる方法は全部で何通りあるか。
どの文字を取り出すかによって、その後の並べ方の計算が変わってきます。
パターンとしては、取り出した文字の中に
- 同じ文字が3個含まれるパターン
- 同じ文字が2個ずつ2組含まれるパターン
- 同じ文字が2個、その他は異なるパターン
(同じ文字が3個含まれるパターン)

(同じ文字が2個ずつ2組含まれるパターン)

(同じ文字が2個、その他は異なるパターン)

以上より、\(8+6+24=38\)通りとなります。
答え
$$38通り$$
同じものを含む円順列・じゅず順列
【問題】
赤球1個,白球2個,青球4個の計7個の球がある。
(1)これらの球を円形に並べる方法は何通りあるか。
(2)これらの球にひもを通して首飾りをつくる方法は何通りあるか。
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
円形に並べるということで、円順列を用いて計算していきます。
円順列の基本は、並べるものを1つ固定することでしたね。
今回のように同じものを含む円順列では、複数あるものではなく、1個しかないものを固定していきましょう。
つまり、1個の赤球を固定して残りの白球2個、青球4個の順列を考えるということになります。
よって、
$$\begin{eqnarray}\frac{6!}{2!4!}=15通り \end{eqnarray}$$
となります。
答え
$$15通り$$
次に首飾りをつくる場合ですが、こちらはじゅず順列を使って考えましょう。
先ほど求めた15通りの中には、裏返したときに同じになるものが含まれていますので、これらを省いていく必要があります。
まず、この15通りの中で球の並びが左右対称になってるもの、そうでないものに分けて考えます。
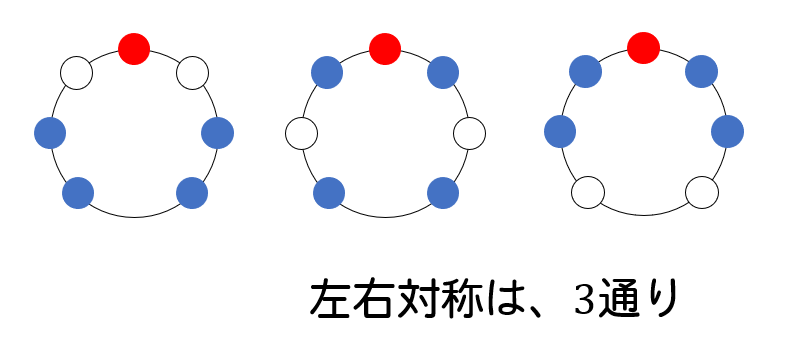
左右対称は上の3通りです。
つまり、左右対称でないものは12通りあるということになります。
そして、左右対称でない並びに関しては、裏返すと同じになる並びが含まれています。
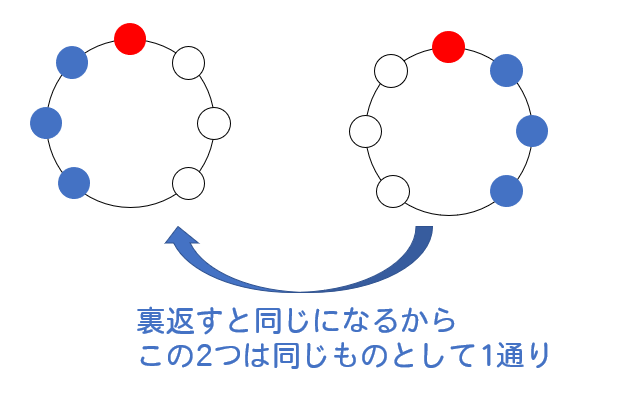
よって、じゅず順列で考える場合、\(12\div2=6\)通りとなります。
以上より、(1)で求めた15通りの中には、
左右対称のものが3通り。
左右対称ではないものが12通り、これは裏返すと同じになるものが含まれているためじゅず順列では6通りとなる。
ということで、\(3+6=9\) 通りとなります。
答え
$$(2) 9通り$$
まとめ!
以上、同じものを含む順列についてでした!
公式の「なぜ」を解決することができたら、
あとはひたすら問題演習をして、様々なパターンに対応できるようにしておきましょう。

- 倍数の個数を求める問題、どうやって考えればいい??
- 集合の要素の個数の問題「できた・できない・どちらも~」
- 集合の要素の個数の最大・最小を求める!イメージ図と不等式を使って考える!
- 3つの集合の要素の個数、イメージ図を使いながら求め方を解説!
- 展開したときの項の数を求め方は?
- 約数の個数と総和を求める公式は?問題を使って解説!
- 硬貨を使って支払える金額は何通り??
- 大中小3つのサイコロを投げるとき何通り?奇数、偶数?4の倍数?
- 順列Pの計算のやり方を簡単にサクッと解説するぞ!
- 3桁、4桁の整数をつくる問題をパターン別に解説!
- 円順列!交互、隣り合う、向かい合うときにはどう考える??
- じゅず順列の解き方はどうやる?円順列との違いは?
- 重複順列の基本問題の解き方をイチから解説するぞ!
- 部分集合の個数の求め方についてイチから解説するぞ!
- 部屋割りの考え方についてイチから解説!
- 平面、空間の塗り分け問題の解き方まとめ!
- 組み合わせCの計算のやり方を簡単にサクッと解説するぞ!
- 平行四辺形は何個ある?考え方を解説!
- 組み分けの場合の数の求め方・考え方をイチから解説!
- なぜ?同じものを含む順列の公式と使い方について問題解説! ←今回の記事
- 重複を許す組み合わせ!Hを使った公式、仕切りを使った考え方を解説!
- サイコロの最大値が5、最小値が2になる確率はどうやって考える?
- 反復試行の確率!なぜこんな公式に?Cを使う理由とは
- 反復試行の確率!3つの事象があるときのやり方は?
- 反復試行の確率!数直線、点の移動を考えるサイコロ問題の解き方は?
- 条件付き確率の考え方を図を使ってイチからわかりやすく!
- 期待値とは?求め方を簡単にサクッと解説!















コメントを残す