【場合の数】平行四辺形は何個ある？いくつある？考え方を解説！

下の図において、平行四辺形はいくつあるか。

 

 

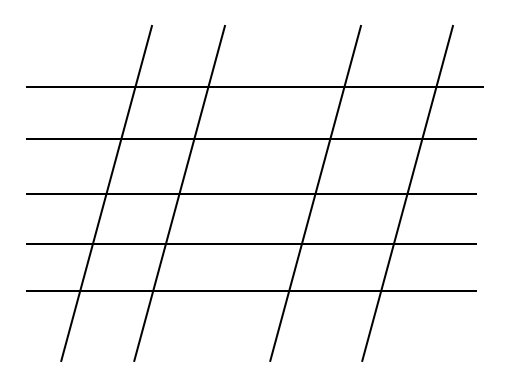
例えば…コレとか

 

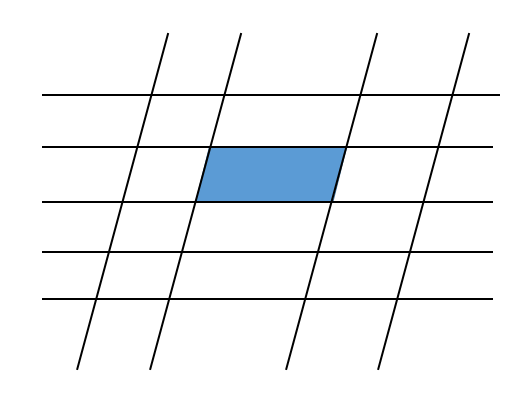
コレとか！

 

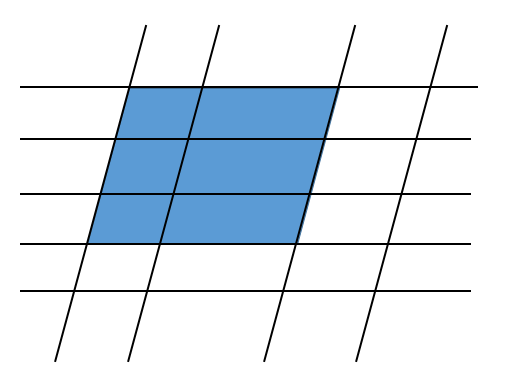
たくさん見つかるよね

これを頑張って数えていけば

平行四辺形が何個できるかを調べることができます。

 

…

 

そんなんめんどいんじゃー！！

ってなっちゃいますので(^^;)

平行四辺形を見つけるための技を伝授しておきます。

 

こちらの動画でサクッと理解できます＾＾

平行四辺形を数えるときのポイント

平行線の中から平行四辺形を見つけるためには

平行線の組み合わせがポイントとなります。

横から２つ、縦から２つずつ線を選ぶと…

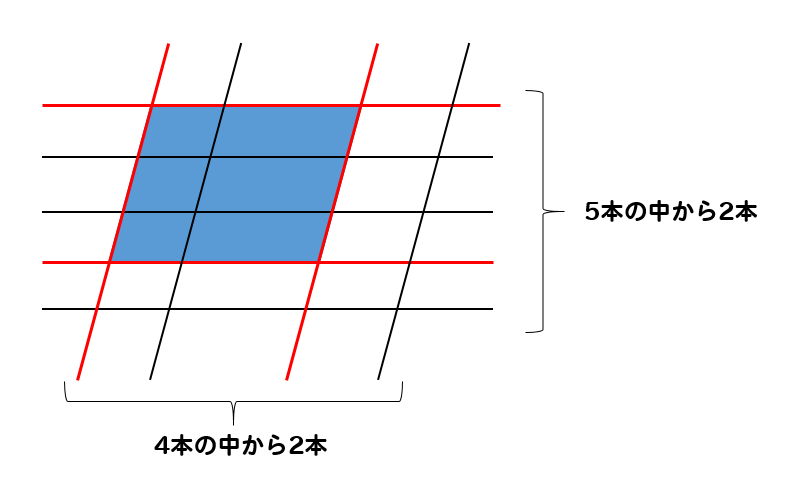
これらの線によって囲まれた部分に、平行四辺形が１つできあがります。

 

 

つまり！

• 平行線の中に平行四辺形が何個あるか
• 縦と横の線から2本ずつ選ぶ組み合わせがいくつあるか

この２つは同じことを考えているということになります。

 

上でやったように、手作業で平行四辺形を見つけていくのは大変です…

だったら、ちょっと見方を変えて線の選び方が何通りあるかを考えていきましょう。

 

以上より

今回の問題の答えは

縦線の選び方が、\({}_5 \mathrm{ C }_2\)

横線の選び方が、\({}_4 \mathrm{ C }_2\)

 

$${}_5 \mathrm{ C }_2\times {}_4 \mathrm{ C }_2=10\times 6=60(個)$$

平行四辺形を見つける練習問題！

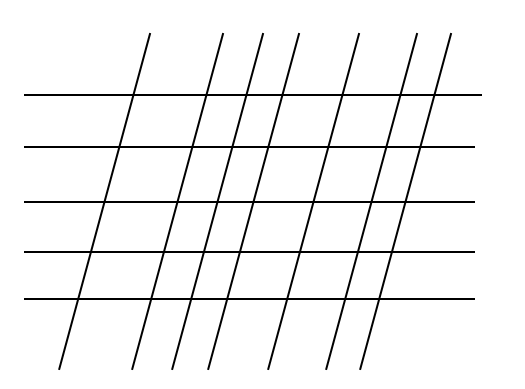
次の図のように、五本の平行線とそれらに交わる七本の平行線がある。

このとき、平行四辺形は何個できるか。

 

まとめ

簡単でしたね！

パッと見ではどうすればいいのか分からないかもしれませんが、ちゃんと考え方を理解すれば楽勝な問題に変わってしまいます(^^)

 

平行四辺形がいくつあるかを考えるときには

タテ、ヨコからそれぞれ2本ずつ選ぶ組み合わせを求める！

というのが解法のポイントでした。

 

以上(/・ω・)/

がんばっているのに60点の壁をクリアできない中3生の方へ

頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。

もしかして、
このような問題に直面していませんか？

僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。
 
すごく勉強したのに試験の結果が36点…
 
「どうすればいいか分からない…」
「点を上げれる自信がない…」
 
自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！
 
なんと、たった2ヶ月で
36点　⇒　72点
なんと、驚きの36点UPを達成！

 
何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。
 
この勉強法を活用した人は、
 
このように次々と良い結果を報告してくれています＾＾
 
Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。
 
そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。
 
こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！
 
もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ