こんにちは!数スタの小田です。
今回はかなりピンポイントな問題になりますが、ご質問いただくことの多いこちらの確率を取り上げます。
【問題】
1から10までの自然数から異なる3個の数を選び出すとき、次の場合の確率を求めなさい。
(1)最大の数が8である。
(2)最大の数が8で、かつ最小の数が4以下
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(1)最大の数が8である
まず、全体の場合の数を求めておきましょう。
10個の数から3個を選ぶので、
\({}_{10} \mathrm{ C }_3=\frac{10\cdot9\cdot8}{3\cdot2\cdot1}=120\)通り
となりますね。
次に最大が8となる場合の数を求めましょう。
最大の数が8ということは、3個取り出される数の内、1つが8で確定します。
そして、残り2個の数は8よりも小さい1~7の中から選ばれることになりますね。(9、10が取り出されると最大が8じゃなくなっちゃうもんね)
というわけで「8を確定させた状態で、残りの2数を1~7の中から2個選ぶ」と考えればよいので
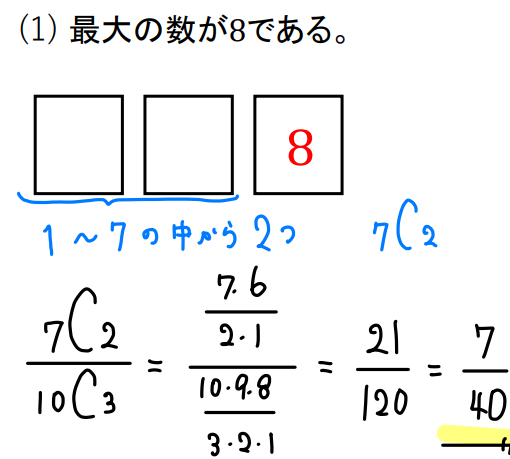
このように求めることができます。
答え
$$\frac{7}{40}$$
(2)最大の数が8で、かつ最小の数が4以下
最小の数が4以下となっているのがポイントですね。
以下ということなので、今回の条件にあてはまるのは
「最大8 かつ 最小1」
「最大8 かつ 最小2」
「最大8 かつ 最小3」
「最大8 かつ 最小4」
このように4つのパターンが考えられますね。
なので、それぞれの場合の数を求めて合計すればOKです。
例えば「最大8 かつ 最小1」となる場合の数は、取り出される3個の数の内、1と8が確定となるので、残り1個の数を2~7の中から1つ選びましょう。
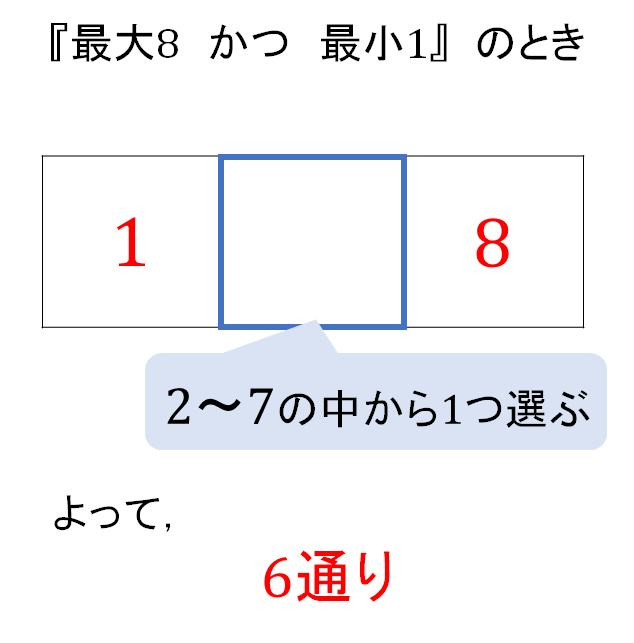
このようにして他のパターンも求めていくと答えが求まります。
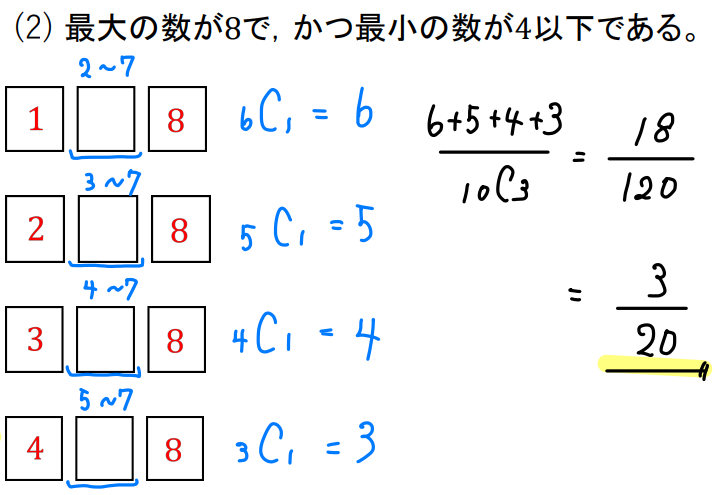
答え
$$\frac{3}{20}$$
この問題に関しては、テキストの解説を見ると余事象を使って考えている場合が多いです。
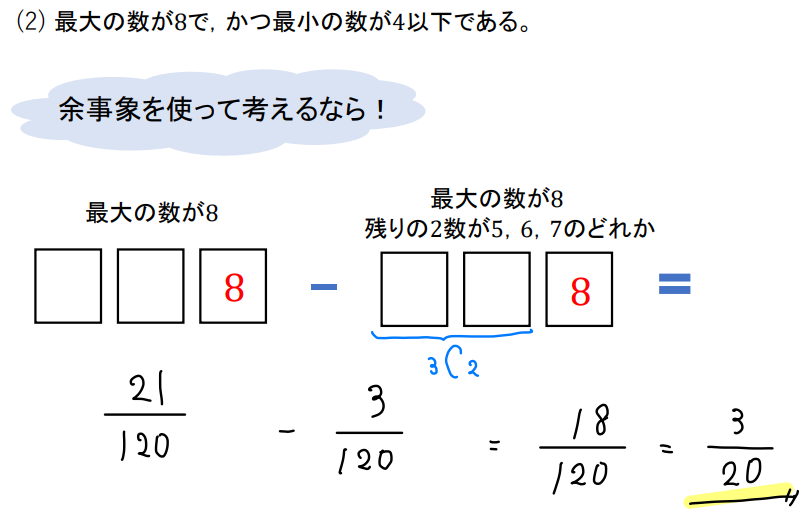
最大が8になっていることを前提として、その中から最小が5,6,7のいずれかになるパターンを取り除くという発想ですね。
ただ…余事象で考えるのってなんか難しくないですか?(^^;)
なので、僕は最初に紹介したように最小値が4以下となるパターンを書き出して、それぞれの場合の数を合計する方がラクに解けるかなって思います!
余事象についての考え方を理解したい方は、冒頭で紹介した動画の中で解説しているので参考にしてみてくださいね^^
というわけで、今回は以上!
最後までお疲れ様でした(‘ω’)ノ
















コメントを残す