3つの集合の要素の個数、イメージ図を使いながら求め方を解説！

高校数学Aで学習する集合の単元から

「3つの集合の要素の個数」

について解説していきます。

集合が3つになるとイメージが難しくなるよね(^^;)

この記事では、画像を使いながら

なるべーくかみ砕きながら解説していきますね！

取り上げる問題はこちら！

【問題】

1から200までの整数のうち，3または5または7で割り切れる数は全部でいくつあるか求めよ。

Contents

3つの集合の和集合の個数を求めるには？
3つの集合の問題解説
ちょっと違ったパターンにも挑戦！
まとめ！

3つの集合の和集合の個数を求めるには？

3つの集合の和集合を求めるにはどうすればよいでしょうか。

まず、2つの集合の場合について確認しておきましょう。

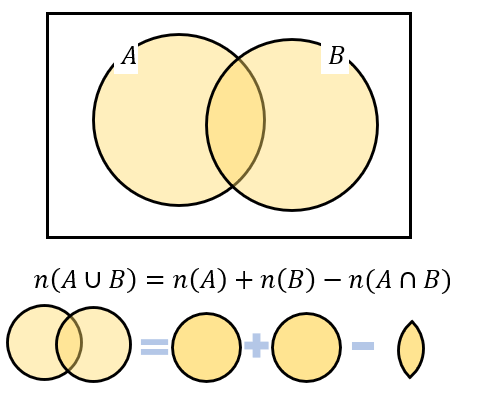
「それぞれの集合の個数を足して、重なっている部分を引く」でしたね。

では、これが3つの集合になると

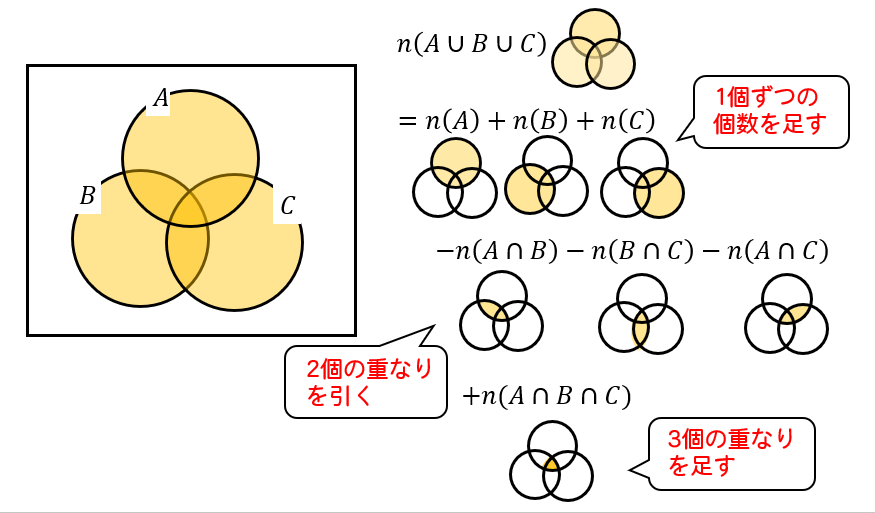
だいぶややこしくなりますが、こんな感じで求めることができます。

まずは、それぞれの集合の個数を足す。

次に、2つの集合が重なっている部分を引く。

最後に、3つの集合が重なっている部分を足す。

という手順になります。

なんで、最後に3つの重なり部分を足す必要があるの？

という疑問をいただくことが多いのですが、

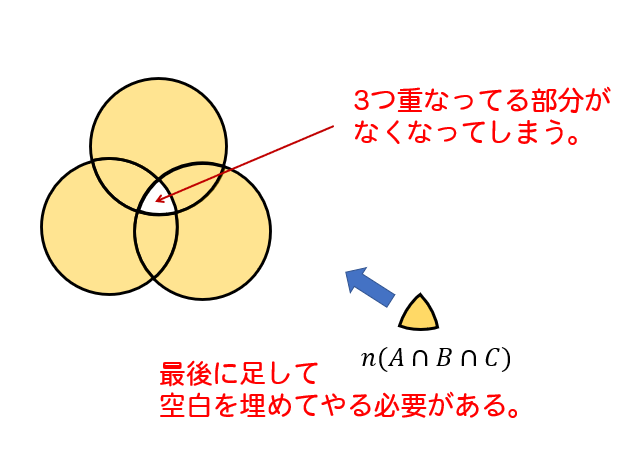
2つの集合が重なっている部分をすべて引いていくと、

上の画像のように、3つ重なっている部分がなくなってしまうんですね。

なので、最後にこの部分を補ってあげる必要があるってわけです。

3つの集合の問題解説

【問題】

1から200までの整数のうち，3または5または7で割り切れる数は全部でいくつあるか求めよ。

3で割り切れる数の集合をAとすると

$A=\{3\cdot 1, \cdots ,3\cdot 66 \}$ ⇒ $n(A)=66$

5で割り切れる数の集合をBとすると

$B=\{5\cdot 1, \cdots ,5\cdot 40 \}$ ⇒ $n(B)=40$

7で割り切れる数の集合をC とすると

$C=\{7\cdot 1, \cdots ,7\cdot 28 \}$ ⇒ $n(C)=28$

$A\cap B$ は3と5の最小公倍数15で割り切れる数の集合だから

$A\cap B=\{15\cdot 1, \cdots ,15\cdot 13 \}$ ⇒ $n(A\cap B)=13$

$B\cap C$ は5と7の最小公倍数35で割り切れる数の集合だから

$B\cap C=\{35\cdot 1, \cdots ,35\cdot 5 \}$ ⇒ $n(B\cap C)=5$

$A\cap C$ は3と7の最小公倍数21で割り切れる数の集合だから

$A\cap C=\{21\cdot 1, \cdots ,21\cdot 9 \}$ ⇒ $n(A\cap C)=9$

$A\cap B\cap C$ は3と5と7の最小公倍数105で割り切れる数の集合だから

$A\cap B\cap C=\{105\cdot 1\}$ ⇒ $n(A\cap B\cap C)=1$

よって、$n(A\cup B\cup C)$ は次のように求めることができます。

$$\begin{eqnarray}&&n(A\cup B\cup C)\\[5pt]&=&n(A)+n(B)+n(C)\\[5pt]&&-n(A\cap B)-n(B \cap C)-n(A\cap C)\\[5pt]&&+n(A\cap B \cap C)\\[5pt]&=&66+40+28-13-5-9+1\\[5pt]&=&108 \end{eqnarray}$$

答え

$$108個$$

ちょっと違ったパターンにも挑戦！

【問題】

3つの集合A，B，Cがある。

$n(U)=100$, $n(A)=50$, $n(B)=13$, $n(C)=30$, $n(A\cap C)=9$

$n(B\cap C)=10$, $n(A\cap B\cap C)=3$, $n(\overline{A}\cap \overline{B}\cap \overline{C})=28$

このとき，$n(A\cap B)$, $n(A\cap\overline{B}\cap \overline{C})$ を求めよ。

まずは、 $n(\overline{A}\cap \overline{B}\cap \overline{C})=28$ から $n(A\cup B\cup C)$ を求めましょう。

$$\begin{eqnarray}n(A\cup B\cup C)&=&n(U)-n(\overline{A}\cap \overline{B}\cap \overline{C})\\[5pt]&=&100-28=72 \end{eqnarray}$$

次に、3つの和集合を求める式に分かっている値を当てはめていきます。

$$\begin{eqnarray}&&n(A\cup B\cup C)\\[5pt]&=&n(A)+n(B)+n(C)\\[5pt]&&-n(A\cap B)-n(B \cap C)-n(A\cap C)\\[5pt]&&+n(A\cap B \cap C)\\[5pt]72&=&50+13+30-n(A\cap B)-10-9+3\\[5pt]n(A\cap B)&=&5 \end{eqnarray}$$

$n(A\cap\overline{B}\cap \overline{C})$ というのは、

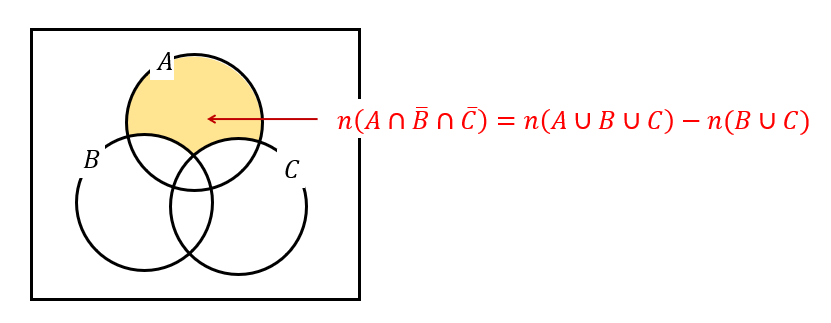
ここの部分のことですね。

つまり、3つの和集合からBとCの和集合を取り除いた部分ということになります。

よって、

$$\begin{eqnarray}&&n(A\cap\overline{B}\cap \overline{C})\\[5pt]&=&n(A\cup B\cup C)-n(B\cup C)\\[5pt]&=&72-\{n(B)+n(C)-n(B\cap C)\}\\[5pt]&=&72-(13+30-10)\\[5pt]&=&39 \end{eqnarray}$$

答え

$$n(A\cap B)=5$$

$$n(A\cap\overline{B}\cap \overline{C})=39$$