今回の記事では「円順列」について解説します。
円順列ってちょっとややこしく感じるよね。
なんで、「－1」するの？
え、ここでは「－１」しないの！？みたいなね(^^;)
というわけで、今回の記事ではパターン別に円順列の問題を解説していくよ！
円順列の基本
【問題】
4人が円形に並ぶ並べ方は何通りあるか。
円形に並べるときには、回転して並びが同じになれば、それは同じものとしてカウントします。
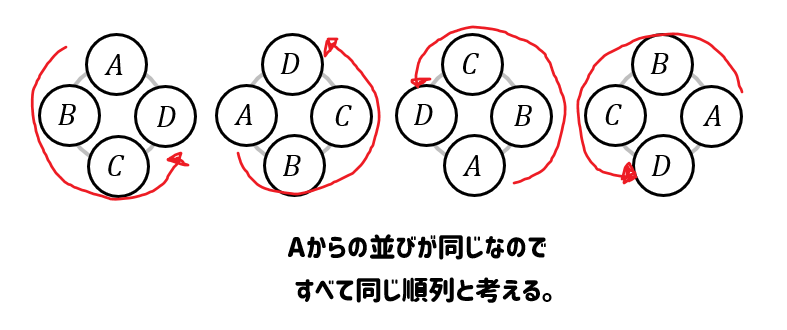
ということは、1つを固定してそれ以外の並びがどうなるかを考えればいいじゃん！
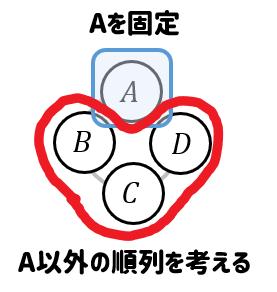
という発想になるんですね。
こうすれば、回転したときに同じ並びになるものを避けて数えることができるようになります。
よって、今回の問題では
1人を固定して、それ以外の3人の順列を考えれば良いので
$$3!=3\cdot2\cdot1=6(通り)\cdots (解)$$
となります。
というわけで一般的に円順列の公式は次のように表されます。
円順列の公式
異なる\(n\)個の円順列の並べ方は
$$(n-1)! 通り$$
円順列（交互に並ぶ）
【問題】
男子4人、女子4人が円形に並ぶとき、男子と女子が交互に並ぶ並び方は何通りあるか。
男子と女子どちらでも良いのですが、まずは1人を固定します。
ここでは男子を固定して話を進めますね。
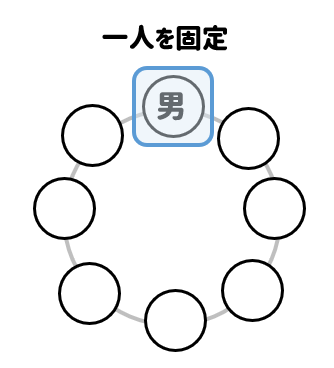
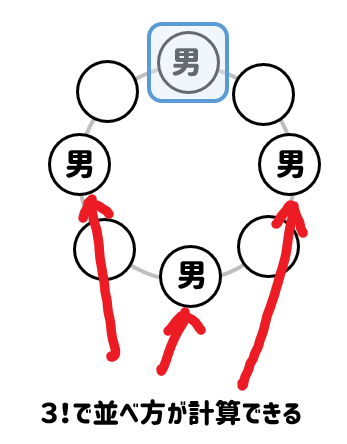
すると、男女を交互に並べるためには、残り3人の男子が入るべきポジションが決まります。
ここに男子3人を並べる並べ方が\(3!\)となります。
最後に、残った4か所に女子4人を並べていけば完成となります。
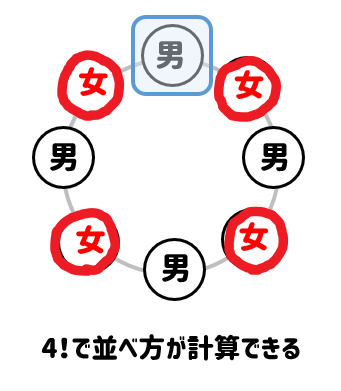
今までの過程を式にして計算すれば答えが求まります。
テキストには次のように書いてあるかもしれませんが、やってることは同じですね。
$$(4-1)!\times 4!=144通り$$
円順列（隣り合う）
【問題】
女子4人と男子2人が円形に並ぶとき、男子が隣り合うような並び方は何通りあるか。
まずは男子A、男子Bを1セットとして固定してしまいましょう。
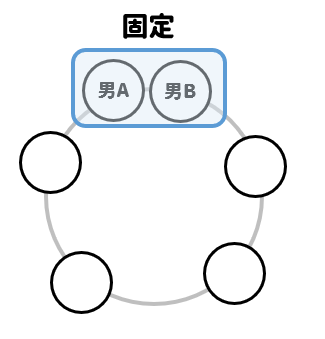
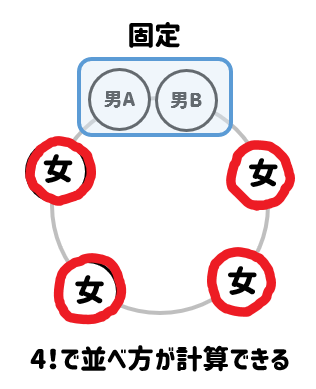
すると、残ったところに4人の女子を並べればよいので
女子の並べ方は4!で計算することができます。
そして、忘れてはならないのが
固定された男子にも順番があることです。
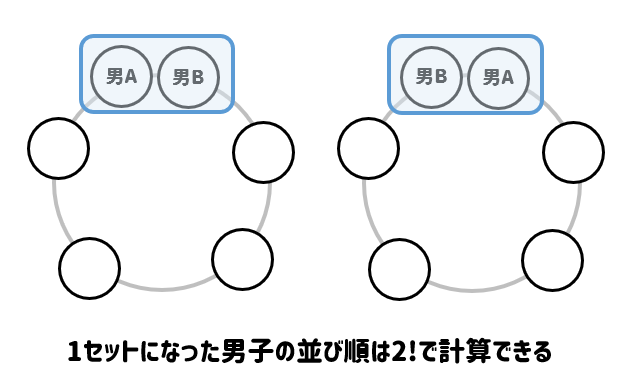
今回は2人だけなので、計算するまでもなく2通りと分かるかもしれませんね。
以上のことから式を作ると次のようになります。
円順列（向かい合う）
【問題】
6個の数字1、2、3、4、5、6を円形に並べるとき、1と2が向かい合って並ぶ並べ方は何通りあるか。
まずは1を固定します。
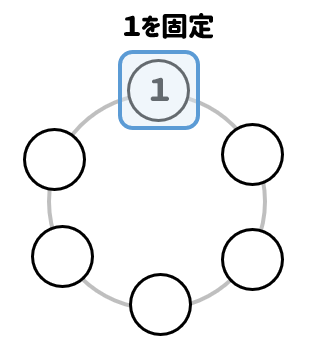
すると、2の位置が自動的に決まりますね。
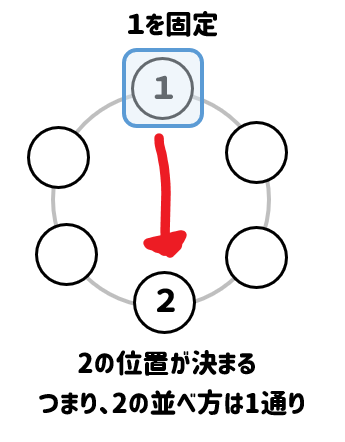
なので、2の並べ方は1通りしかないってことです。
あとは、残ったところに3、4、5、6を並べればOKです。
よって、式は次のようになります。
まとめ！
お疲れ様でした(^^)
円順列では「ダブりを防ぐために固定してから考え始める」というのがポイントです。
どのパターンも計算はすごく簡単です。
発想を身につけてしまえばこっちのもんですね！
というわけで、たくさん練習問題を解いて理解力を高めておきましょう(/・ω・)/
数スタのオリジナル教材を販売中！
数スタのオリジナル教材を作成しました。
第1弾は高校入試対策、規則性の教材です。
苦手にしている人が多い単元ですが、
コツを掴むと簡単に解けるようになります。
⇒ 【高校入試】規則性の問題をゼロから＋10点する教材
