【反復試行の確率】3つの事象があるときのやり方は？

今回は高校数学Aで学習する確率の単元から

『3つの事象がある反復試行の確率』

について解説していきます。

取り上げる問題はこちらだ！

赤玉1個と白玉2個と青玉3個が入った袋から1個の玉を取り出し、色を調べてからもとに戻す。これを5回行うとき、赤玉が1回、白玉が2回、青玉が2回出る確率を求めよ。

今回の内容はこちらの動画でも解説しています！

Contents

3種類あるときの反復試行　考え方と解説！
練習問題で理解を深める！
まとめ！
がんばっているのに60点の壁をクリアできない中3生の方へ
- こちらの関連記事はいかがでしょうか？

3種類あるときの反復試行　考え方と解説！

反復試行の公式といえば

反復試行の公式
1回の施行で事象Aの起こる確率が$p$で、この試行を$n$回繰り返し行うとき、Aがちょうど$r$回起こる確率は
$$\large{{}_n \mathrm{ C }_rp^rq^{n-r}}$$

これでしたね。

だけど、今回の問題のように

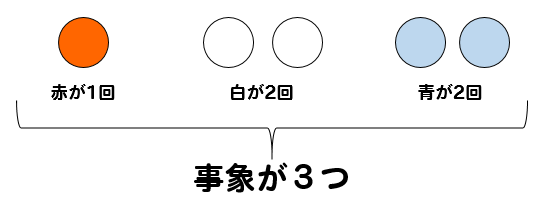
事象が3つある場合を考えるときには、ちょっと工夫して公式を利用していく必要があります。

反復試行の公式について不安がある方は、こちらの記事で確認しておいてね。

＞【反復試行の確率】なぜこんな公式になるの？Cを使う理由は？

まず、赤玉が1回、白玉が2回、青玉が2回出るというのが何通りあるか考えてみましょう。

すると、こんな感じで…たくさんありすぎて手作業で数えるのは厳しいですね(^^;)

なんとか、計算で求めたい。

そこで利用するのがやっぱり

Cです。

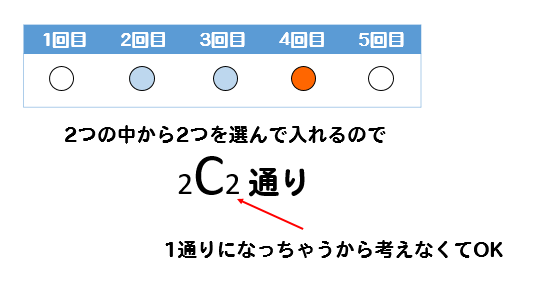
まず、5つの中から赤玉が出る場所を決めます。

それが、${}_5 \mathrm{ C }_1$です。

次に、残った4つの中から白が出るところを2つ選びます。

それが、${}_4 \mathrm{ C }_2$です。

青玉2つは、残ったところに自動的に入ることとなるので考える必要はありません。

これらのことをまとめて考えると

5回中、赤玉が1回、白玉が2回、青玉が2回出るのは

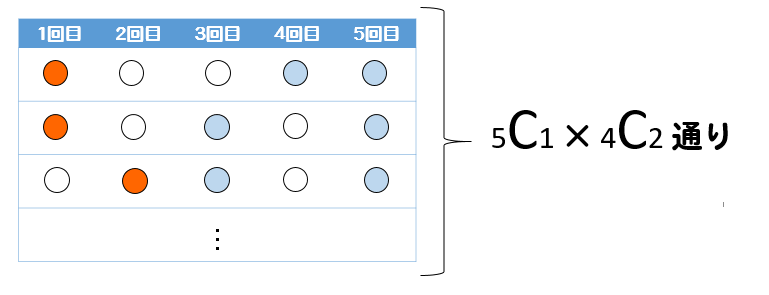
このようになります。

あとは、簡単！

赤玉が出る確率が、$\displaystyle{\frac{1}{6}}$

白玉が出る確率が、$\displaystyle{\frac{2}{6}}=\frac{1}{3}$

青玉が出る確率が、$\displaystyle{\frac{3}{6}}=\frac{1}{2}$

であることを利用すると

$${}_5 \mathrm{ C }_1\times {}_4 \mathrm{ C }_2\left(\frac{1}{6}\right)^1\left(\frac{1}{3}\right)^2\left(\frac{1}{2}\right)^2$$

$$=5\times 6\times \frac{1}{6}\times \frac{1}{9}\times \frac{1}{4}$$

$$=\frac{5}{36}$$

答え

$$\frac{5}{36}$$

いかがでしたでしょうか？

考え方は、事象が2つの場合と同じなんだけど全部でパターンがいくつあるかを考える場合にCを2回使う必要があります。

なので、反復試行の公式を意味を理解せずに丸暗記してしまっている人にとっては分かりにくい問題となっています。

また、Cを使わずに数える方法もあります。

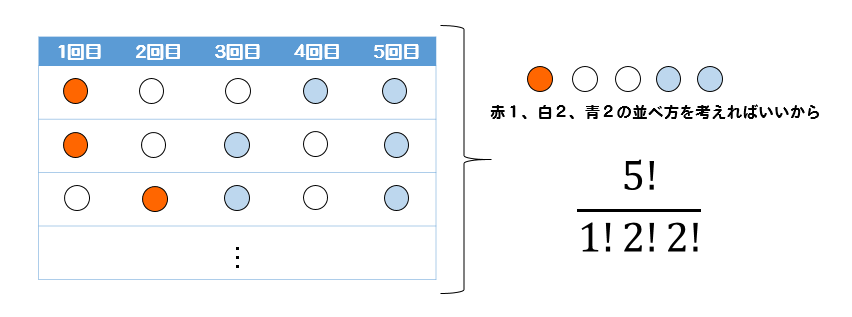
それが、このように順列を使って考える方法です。

もちろん、どちらも同じ値になりますので自分がしっくりくるやり方を身につけてください。

それでは、理解を深めるため練習問題に挑戦だ！

練習問題で理解を深める！

赤玉1個、青玉3個、白玉2個が入った袋の中から玉を1個取り出してはもとに戻すという操作を5回繰り返すとき、赤玉が1回、青玉が3回、白玉が1回取り出される確率を求めよ。

解説＆答えはこちら

答え

$$\frac{5}{36}$$

まず、赤玉が出る確率は$\displaystyle{\frac{1}{6}}$であり、青玉が出る確率は$\displaystyle{\frac{1}{2}}$、白玉が出る確率は$\displaystyle{\frac{1}{3}}$となります。

これを用いて考えると

$${}_5 \mathrm{ C }_1\times {}_4 \mathrm{ C }_3\left(\frac{1}{6}\right)^1\left(\frac{1}{2}\right)^3\left(\frac{1}{3}\right)^1$$

$$=5\times 4\times \frac{1}{6}\times \frac{1}{8}\times \frac{1}{3}$$

$$=\frac{5}{36}$$

まとめ！

お疲れ様でした！

事象が3つある場合の反復試行は、何通りあるか考えるところがポイントですね。

Cを2回使って考える、もしくは順列を使って考えていくと良いでしょう。

ファイトだ(/・ω・)/

こちらの記事も合わせてどうぞ！

がんばっているのに60点の壁をクリアできない中3生の方へ

頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。

もしかして、
このような問題に直面していませんか？

模試になると点がガクッと落ちる
復習のやり方が分からない
勉強してもすぐに忘れる
凡ミスが直らない
家だと集中して勉強できない
問題集を買っても、1人で解けなくて途中でやめてしまう
友人が点を伸ばしていて焦る
頑張りたいから何をすればいいか教えて欲しい

僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。

すごく勉強したのに試験の結果が36点…

「どうすればいいか分からない…」
「点を上げれる自信がない…」

自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！

なんと、たった2ヶ月で
36点　⇒　72点
なんと、驚きの36点UPを達成！

何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。

この勉強法を活用した人は、

43点　⇒　69点

67点　⇒　94点

人生初の100点！

このように次々と良い結果を報告してくれています＾＾

Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。

そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。

こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！

もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ

無料でワークをもらう！

数スタの他記事はこちらから