高校数学Aで学習する場合の数の単元から
「平面、立体の塗り分け」
についての問題をまとめておきます。
今回の記事を通して、問題の解き方を身につけていきましょう。
取り上げる問題はこちら！
【問題①】
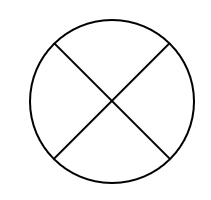
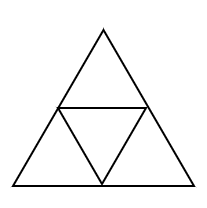
下の図のように4個の部分に区切った紙を、4色の絵の具をすべて使って塗り分ける方法は何通りあるか。
（1）
（2）
【問題②】
下のA，B，C，D，Eの5つの四角形を，次の色すべてを用いて塗る方法は何通りあるか。ただし，隣り合う四角形は異なる色を塗るものとする。
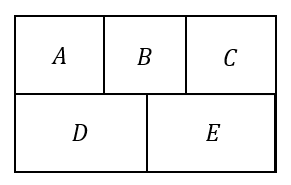
（1）5色
（2）4色
（3）3色
【問題③】
下の図のA，B，C，D，Eの5つの部分を，次の色すべてを用いて塗る方法は何通りあるか。ただし，隣り合う部分は異なる色を塗るものとする。
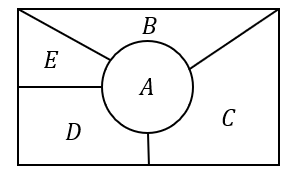
（1）5色
（2）4色
（3）3色
【問題④】
下の図のA，B，C，D，E，Fの6つの部分を，次の色すべてを用いて塗る方法は何通りあるか。ただし，隣り合う部分は異なる色を塗るものとする。
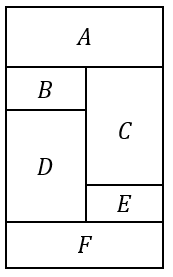
（1）3色
（2）4色
【問題⑤】
立方体の6つの面を次の色すべてを用いて塗る方法は何通りあるか。ただし，立方体を回転させて一致する塗り方は同じものとみなし，隣り合う面は異なる色を塗るものとする。
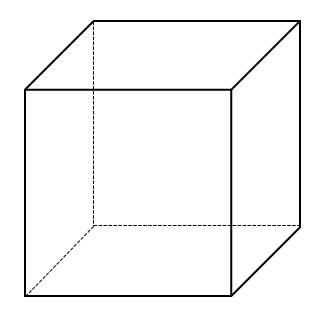
（1）赤，青，白，黒，緑，黄の6色
（2）赤，青，白，黒，緑の5色
（3）赤，青，白，黒の4色
（4）赤，青，白の3色
【問題⑥】
正四角錐の5つの面を次のように塗る方法は何通りあるか。ただし，回転させて一致する塗り方は同じものとみなし，隣り合う面は異なる色を塗るものとする。
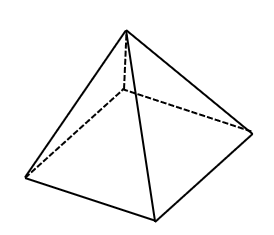
（1）異なる5色をすべて用いて塗る方法
（2）異なる4色をすべて用いて塗る方法
（3）異なる3色をすべて用いて塗る方法
平面塗り分け【問題①】
下の図のように4個の部分に区切った紙を、4色の絵の具をすべて使って塗り分ける方法は何通りあるか。
（1）
円形であり、回転させたときに同じ形になるので、これは円順列として考えていきます。
4色の円順列だから、\((4-1)!=3\cdot 2\cdot 1=6\) 通りとなります。
答え
$$(1) 6通り$$
まずは中央部分の塗り方を考えましょう。
4色を使うので、中央の塗り方は4通りとなります。
そして、周りの3ヵ所に関しては円順列となるので、\((3-1)!=2\) 通り。
よって、\(4\times 2=8\) 通りとなります。
答え
$$(2) 8通り$$
平面塗り分け【問題②】
下のA，B，C，D，Eの5つの四角形を，次の色すべてを用いて塗る方法は何通りあるか。ただし，隣り合う四角形は異なる色を塗るものとする。
（1）5色
塗る部分と色の数が同じときには簡単ですね。
求める塗り方は、5色の順列と同じになります。
よって、\(5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120\) 通り。
答え
$$(1) 120通り$$
4色のときには、1色だけ2ヵ所に塗る必要があります。
また、隣り合う部分は異なる色でなければなりませんので、
このようなパターンが考えられます。
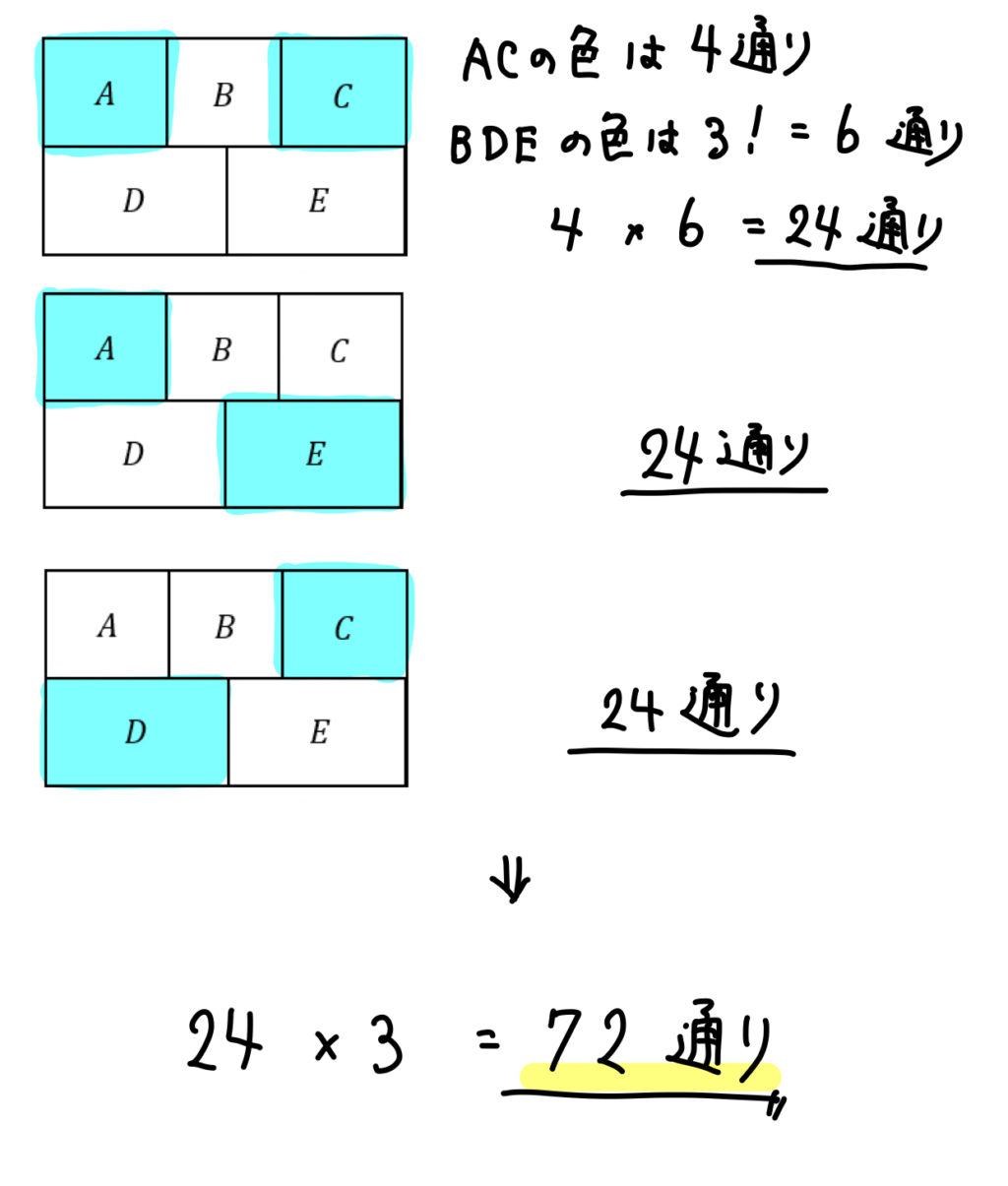
同じ色を塗ることができるのは、AC，AE，CDの3パターン。
2ヵ所に塗る色の選び方が4通り。残った部分の塗り方が \(3!=6\) 通り。
よって、\(3\times 4\times 6=72\)通り。
答え
$$(2) 72通り$$
3色を使って塗るには、2色をそれぞれ2ヵ所に塗る必要があります。
隣り合う部分が異なる色であることから、塗り方は次の1パターンのみになります。
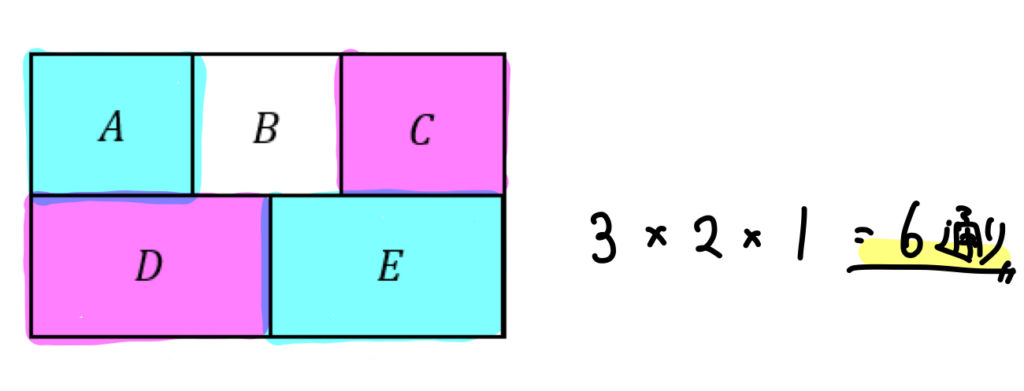
この配置で3色を塗るには、AE，CD，Bの3ヵ所を3色で塗る方法として考えればよいですね。
よって、\(3!=6\)通り。
答え
$$(3) 6通り$$
平面塗り分け【問題③】
下の図のA，B，C，D，Eの5つの部分を，次の色すべてを用いて塗る方法は何通りあるか。ただし，隣り合う部分は異なる色を塗るものとする。
（1）5色
5ヵ所に5色なので、そのまま順列を考えればよいですね。
\(5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120\)通りとなります。
答え
$$(1) 120通り$$
4色のうち1色を2ヵ所に塗る必要があります。
塗り方のパターンとしては次のようになります。
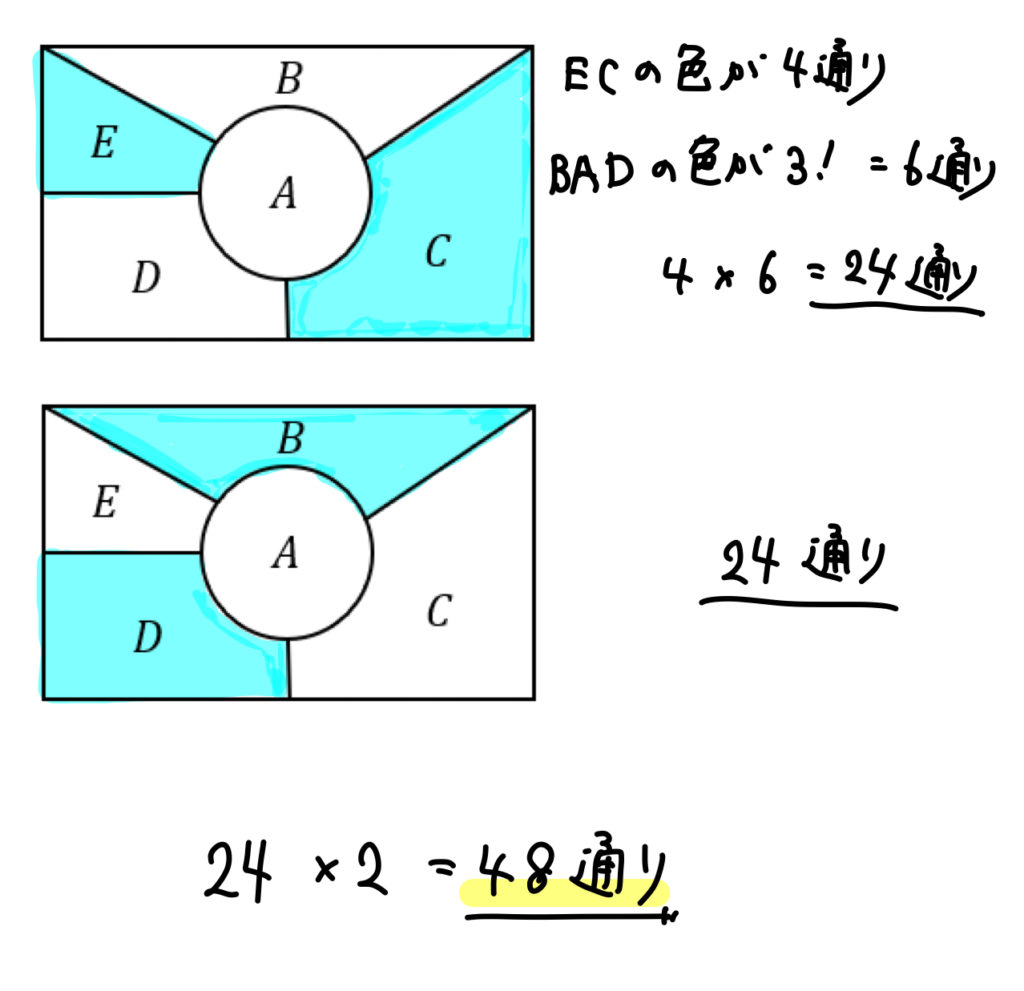
同じ色を塗ることができるのは、EC，BDの2パターン。
2ヵ所に塗る色の選び方が4通り。残った部分の塗り方が \(3!=6\) 通り。
よって、\(2\times 4\times 6=48\)通り。
答え
$$(2) 48通り$$
3色を使って塗るには、2色をそれぞれ2ヵ所に塗る必要があります。
隣り合う部分が異なる色であることから、塗り方は次の1パターンのみになります。
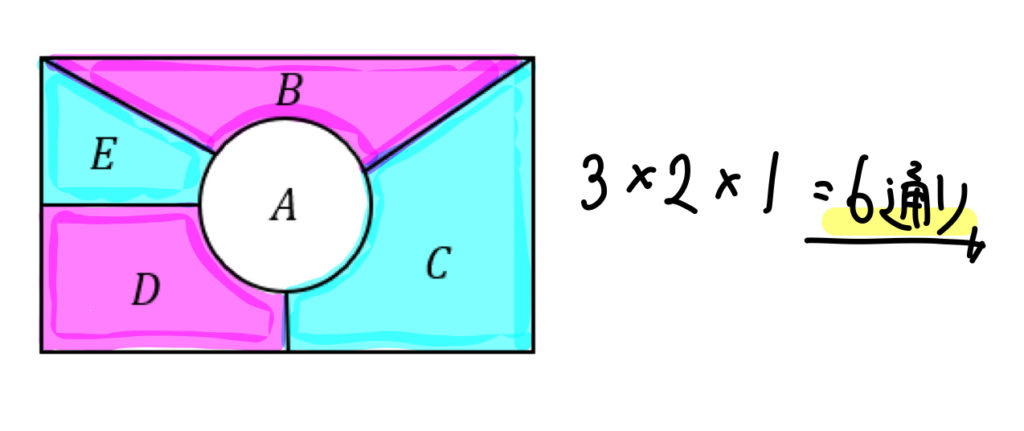
この配置で3色を塗るには、BD，EC，Aの3ヵ所を3色で塗る方法として考えればよいですね。
よって、\(3!=6\)通り。
答え
$$(3) 6通り$$
平面塗り分け【問題④】
下の図のA，B，C，D，E，Fの6つの部分を，次の色すべてを用いて塗る方法は何通りあるか。ただし，隣り合う部分は異なる色を塗るものとする。
（1）3色
3色で塗るためには、下の図のようにAD，BE，CFを同じ色で塗る必要があります。
よって、AD，BE，CFを3色で塗る方法として、\(3!=6\)通りと計算すればよいですね。
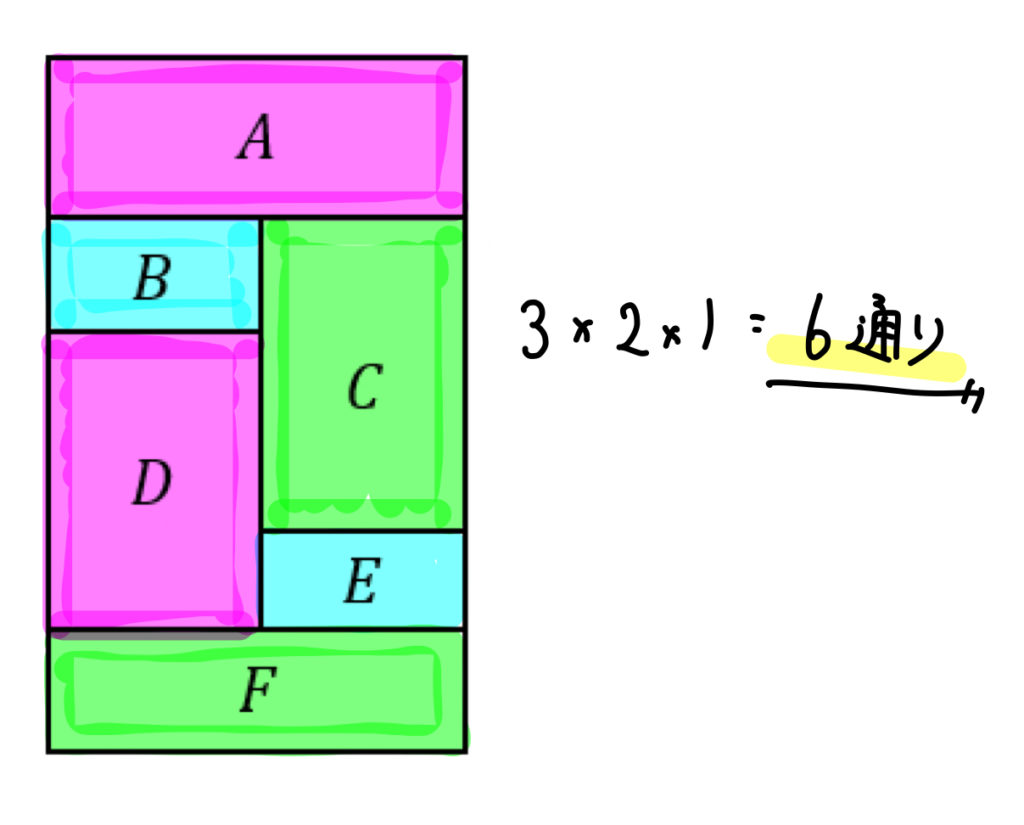
答え
$$6通り$$
4色で塗るのは、ちょっとパターンがたくさんあります。
まずは、A，B，Cの部分に注目してみましょう。
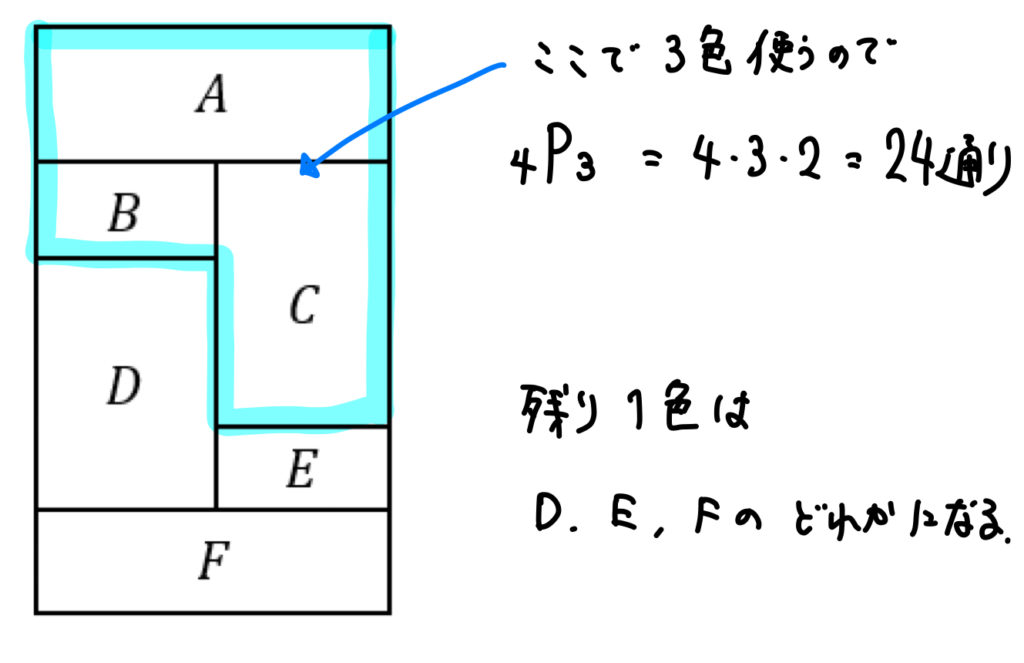
ここはすべて隣接しているので、色を塗るには3色が必要になります。
なので、まずはこの部分に色を塗るのに何通りあるかを計算しておきます。
これが \(3!=6\)通りとなります。
次に、4色目をどこに塗るのか？という視点で考えていきます。
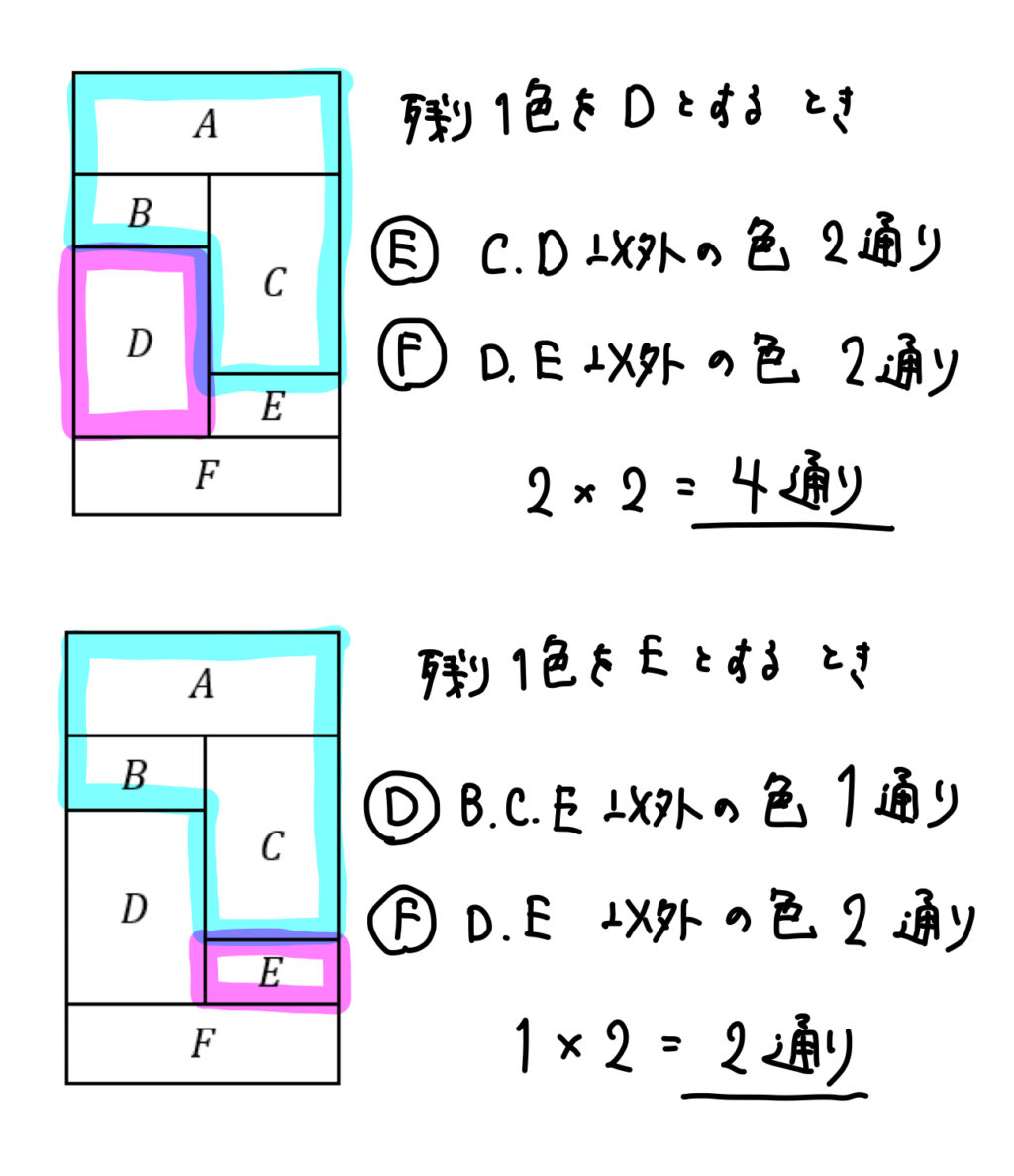
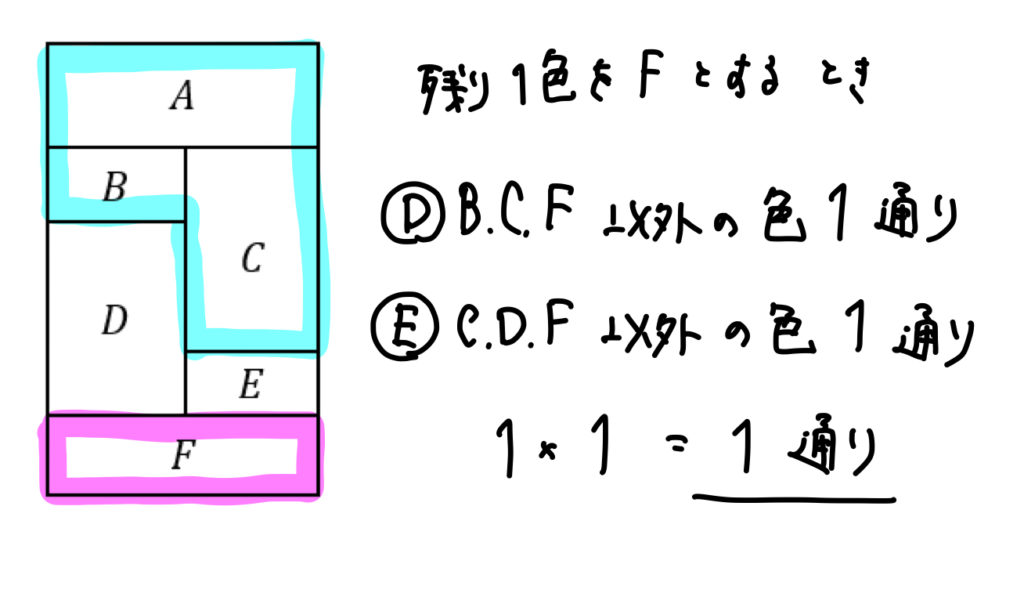
すると、このように4色目はD，E，Fのいずれかに塗るっていう3パターンが考えられます。
以上のことをまとめると、
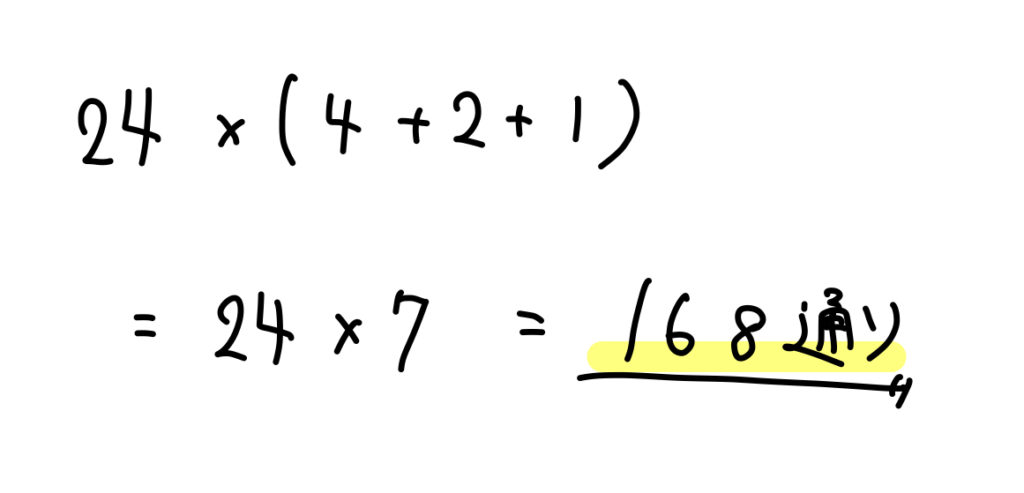
となります。
答え
$$168通り$$
空間塗り分け【問題⑤】
立方体の6つの面を次の色すべてを用いて塗る方法は何通りあるか。ただし，立方体を回転させて一致する塗り方は同じものとみなし，隣り合う面は異なる色を塗るものとする。
（1）赤，青，白，黒，緑，黄の6色
空間の塗り分けを考える場合、立体を回転したときに同じとみなされるものが出てくるので注意が必要です。
まずは、上面の色を固定してから考えていきましょう。
そこから対面の色を決める。
最後に側面を円順列で考えるという流れになります。
回転したときに同じになるものを省くため、側面は円順列を用います。
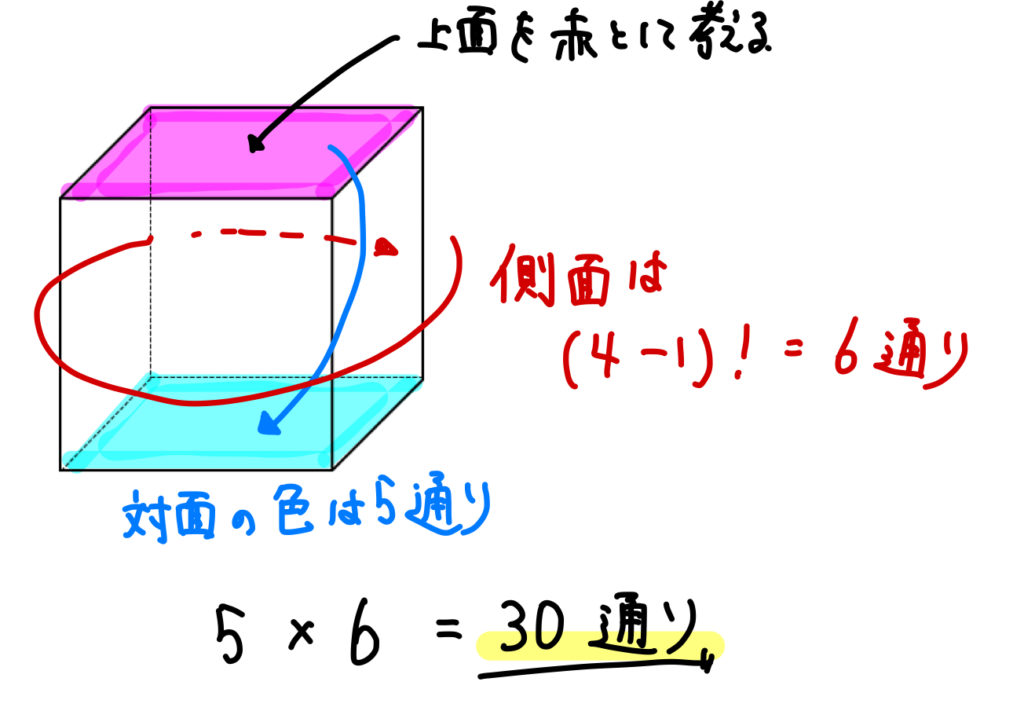
答え
$$30通り$$
5色で塗る場合には、1色だけ2面に塗る必要があります。
この色の塗り方は必ず向かい合った面になります。
また、対面が同じ色になっている場合には、回転だけでなく、ひっくり返したときにも同じ色の塗り方と考えることができます。
よって、側面はじゅず順列を使って計算していきましょう。
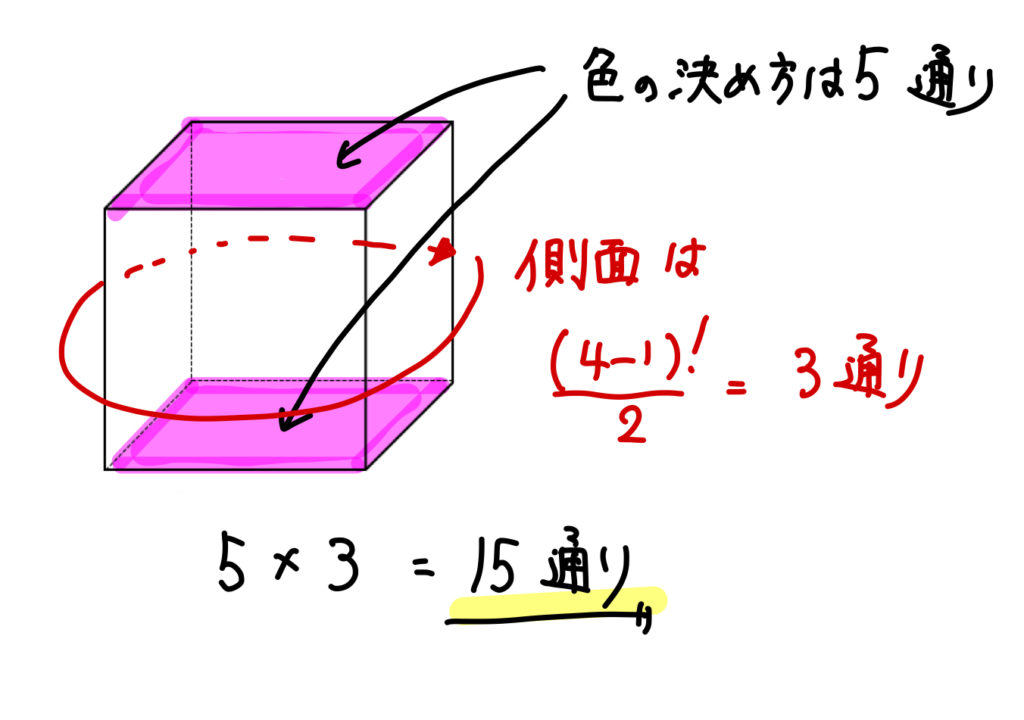
答え
$$15通り$$
4色で塗るためには、2色を2面ずつ塗る必要があります。
どの色を2面ずつにするのかの選び方が6通り。
残った2面の塗り方は、ひっくり返したときに同じことを考慮すると1通りとなります。
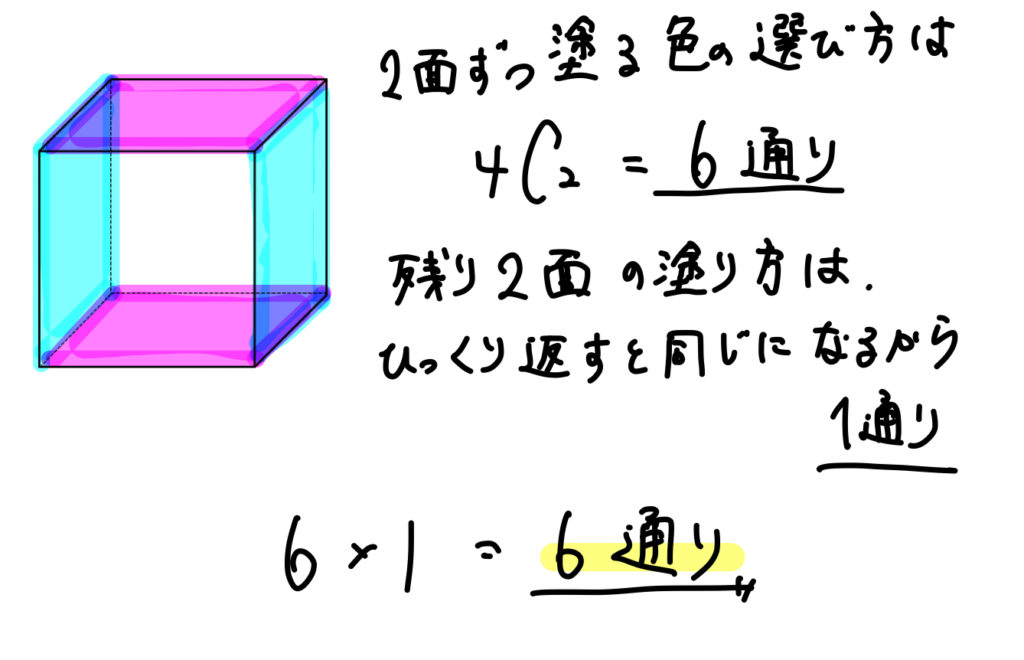
答え
$$6通り$$
3色で塗る場合には、それぞれの色を対面で塗る必要があるので1通りだけになります。
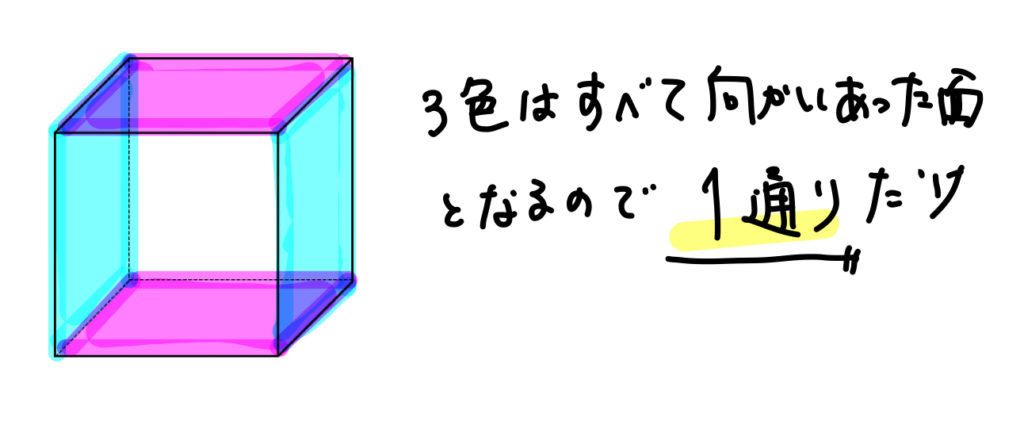
答え
$$1通り$$
空間塗り分け【問題⑥】
正四角錐の5つの面を次のように塗る方法は何通りあるか。ただし，回転させて一致する塗り方は同じものとみなし，隣り合う面は異なる色を塗るものとする。
（1）異なる5色をすべて用いて塗る方法
まずは底面の色の塗り方を考えます。
そして、側面は円順列で考えていきましょう。
四角錐は、立方体と違いひっくり返した場合を考える必要がないのがポイントですね。
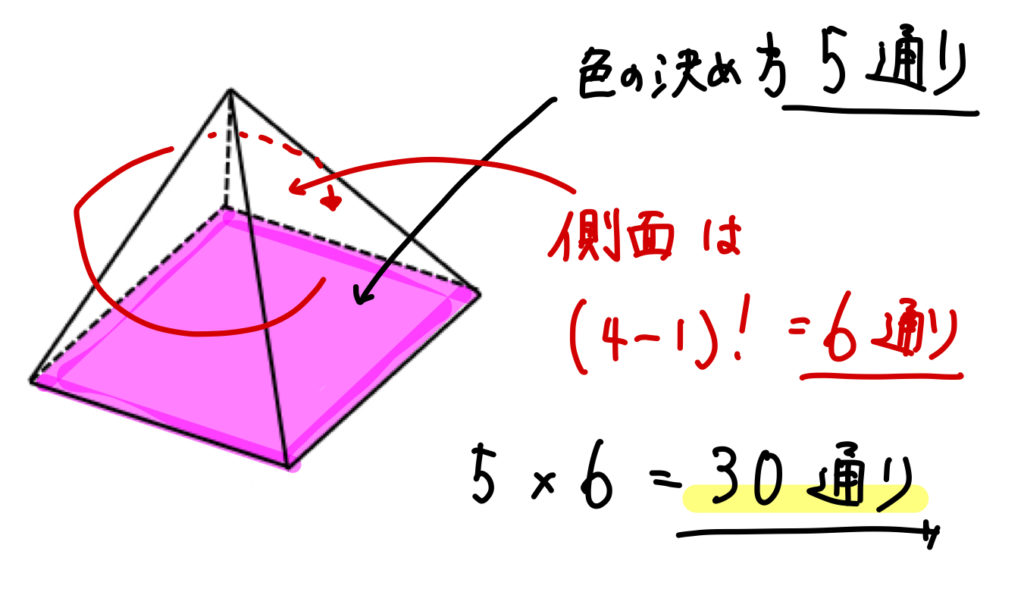
答え
$$30通り$$
4色で塗るためには、1色を側面の向かい合うところに塗る必要があります。
これの色の決め方が4通り。
次に底面の塗り方は残りが3色なので、3通り。
すると、残った側面2つに2色を塗ることになるんだけど、回転させたときに一致することを考えると1通りとなります。
答え
$$12通り$$
まずは底面の塗り方を考える。これが3通り。
すると、残った2色は側面の向かい合うところに塗る必要があるので、これは1通り。
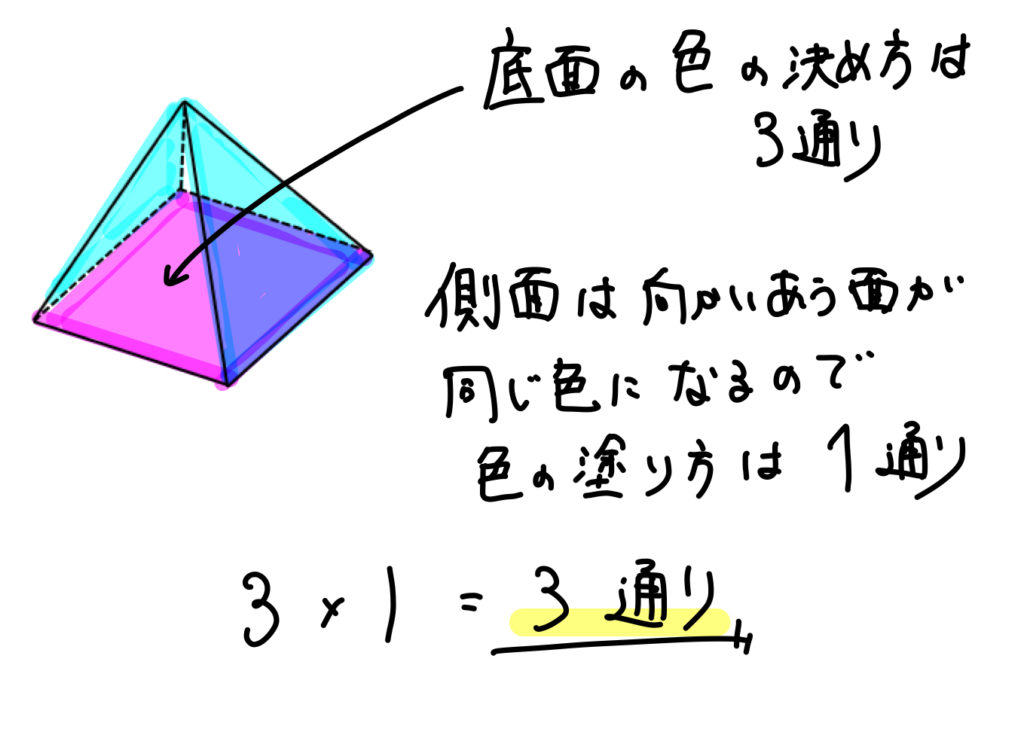
答え
$$3通り$$
まとめ！
お疲れ様でした！
塗り分け問題では、どの部分が同じ色になる？
ここは円順列？じゅず順列？といった判断が難しいですよね。
たくさんの問題を解くことで、
あ、ここが同じ色、円順列だ！っていう感覚が身につくはずです。
ってことで、演習あるのみだ(/・ω・)/
コメントを残す