【数学A】サイコロの最大値が5、最小値が2になる確率はどうやって考える？

高校数学Aで学習する確率の単元から

「さいころの目の最大値・最小値」

について解説していきます。

取り上げる問題はこちら！

今回の内容はこちらの動画でも解説しています！

さいころの目の最大値が3以下、3になる確率

まず、4個のさいころを同時に投げるとき

すべての目の出方は、\(6^4\)  通りとなります。

あとで分数に形にして約分できることを考えて、\(6^4\)は計算せず、このままの形にしておきます。

次に、さいころの目の最大値が3以下というのは、

どの目も \(1,2,3\) (3通り)のどれかということになります。

よって、目の出方は \(3^4\) 通りですね。

以上より、求める確率は

\(\frac{3^4}{6^4}=\left(\frac{3}{6} \right)^4=\left(\frac{1}{2} \right)^4=\frac{1}{16}\)

目の最大値が3以下となる確率には、

最大値が3になる場合、2になる場合、1になる場合

これらがすべて含まれた状態になります。

では、こちらの問題では

先ほどの最大値が3以下になる場合から

最大値が2になる、1になる場合（最大値が2以下となる）を引いてやればよいと考えます。

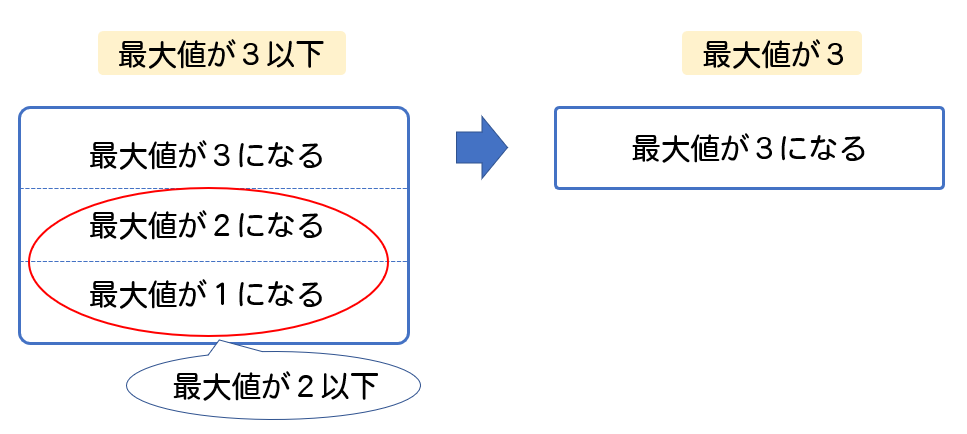
最大値が2以下となる確率は（1）と同様に、

\(\frac{2^4}{6^4}=\left(\frac{2}{6} \right)^4=\left(\frac{1}{3} \right)^4=\frac{1}{81}\)

以上より、

\(\frac{1}{16}-\frac{1}{81}=\frac{65}{1296}\)

では、さいころの最大値を求めるポイントをまとめておきます。

【さいころの最大値】

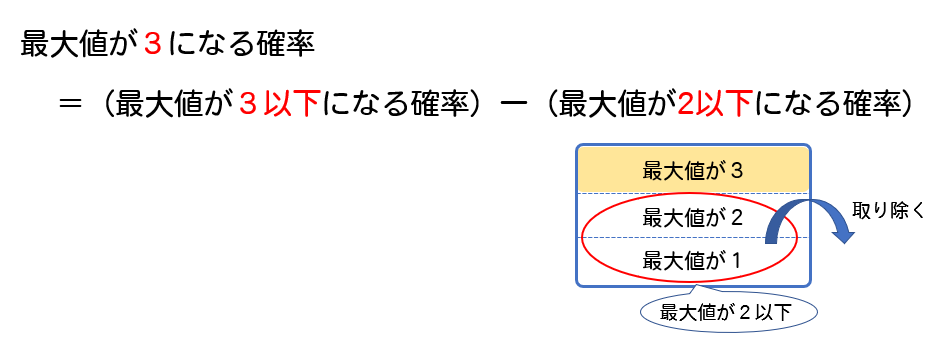
【さいころの最小値】

さいころの目の最大値が5，最小値が2となる確率

最大値と最小値を同時に指定される場合は、

ちょっと考え方が難しくなります。

考え方のイメージとしては、こんな感じ！

目の最大値が5，最小値が2ってことは、1と6の目は出てこない。

ってことで、2，3，4，5 の 4つの目がいずれかが出る確率を考える。

⇒　 \(\frac{4^3}{6^3}=\left(\frac{2}{3}\right)^3=\frac{8}{27}\)

ただし、この場合の数の中には、

\((3,4,5)\) のように2の目が出ていないからダメ

⇒　3, 4, 5 のいずれかしか使われていないAパターン。

\((2,3,3)\) のように 5の目が出ていないからダメ

⇒　2, 3, 4 のいずれかしか使われていないBパターン。

以上の2パターンが含まれていることになります。

なので、

2，3，4，5 の 4つの目がいずれかが出る確率から

AパターンまたはBパターンを取り除いてやればいいと考えます。

AまたはBを取り除くときには、「AかつB」の部分があることに気を付けてください。

すると、

パターンA（2，3，4のいずれかの目が出る）の確率

⇒ \(\frac{3^3}{6^3}=\left(\frac{1}{2}\right)^3=\frac{1}{8}\)

パターンB（3，4，5のいずれかの目が出る）の確率

⇒ \(\frac{3^3}{6^3}=\left(\frac{1}{2}\right)^3=\frac{1}{8}\)

パターンAかつB（3，4のどちらかの目が出る）の確率

⇒ \(\frac{2^3}{6^3}=\left(\frac{1}{3}\right)^3=\frac{1}{27}\)

以上より、

$$\begin{eqnarray} &&\frac{8}{27}-\left(\frac{1}{8}+\frac{1}{8}-\frac{1}{27}\right)\\[5pt]&=&\frac{1}{12}\end{eqnarray}$$

最小値、最大値が与えられたときのポイントをまとめておきます。

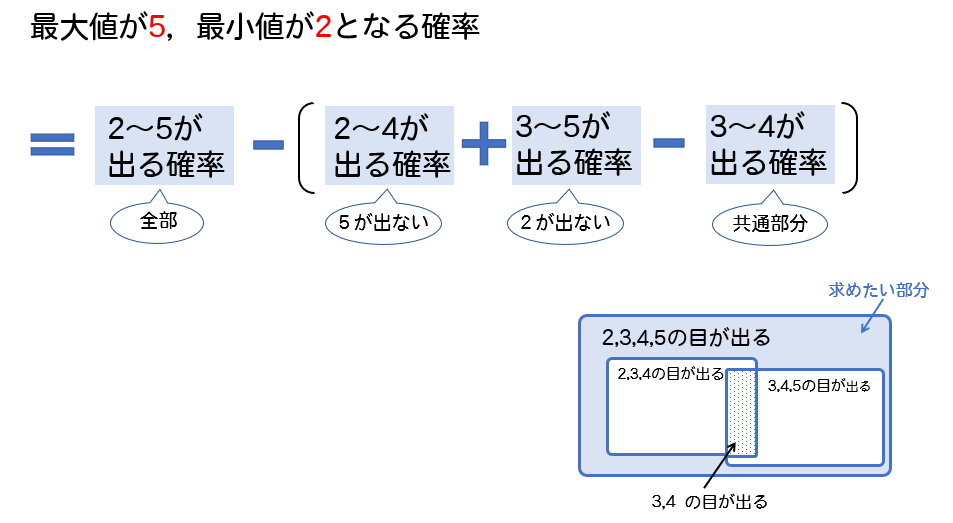
まとめ！

お疲れ様でした！

最大値、最小値がともに与えられた場合がちょっと難しいですね(^^;)

以下の画像を元に、最大・最小のイメージを固めておいてくださいね！