【苦手な人向け】順列Pの計算のやり方を簡単にサクッと解説するぞ！

今回の記事では高校数学Aで学習する

「順列Pの計算のやり方」

についてイチから解説していくよ。

この記事を通して、次のようなPの計算ができるようになろう！

そして、順列Pが表している意味についても理解しておこう！

順列Pの計算方法をサクッと理解したい方は、こちらの動画をどうぞ！

順列Pの計算のやり方

順列Pの計算のやり方についてサクッと理解しておきましょう。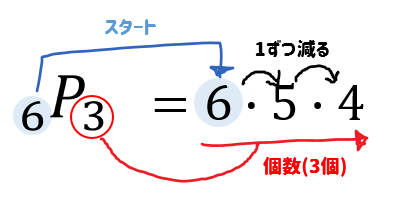

左の数から始まり、1つずつ数を減らしながら右の数だけ掛け算をしていきます。

上の式であれば、「６ピー３」と読みます。

文字で書くとなんだか変な感じだけどね

６と３の間に何が起きたんだ！みたいなｗ

順列Pの基本計算

では、次の計算がどうなるかを確認してみましょう。

簡単ですね！

計算ミスだけ気をつければ簡単に答えが出せます(^^)

階乗！の計算

そして、追加で覚えておきたいことがあります。

（2）の問題のように左と右の数が同じになる場合

このように！を使って表すことができます。

これを4の階乗（かいじょう）と読みます。

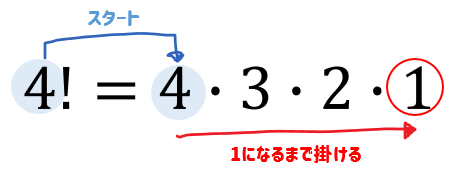
階乗とは、スタートの数から1つずつ減らしていき、その数が1になるまで掛け続けるって意味です。

では、次の問題がどうなるか分かるかな？

6の階乗なので、スタートは6でゴールは1となります。

$$6!=6\cdot5\cdot4\cdot3\cdot2\cdot1=720\cdots(解)$$

となります。

計算部分は大変なので、頑張ってくれ(/・ω・)/

覚えておきたい０の計算

0が含まれている場合の計算はどうなるのでしょうか。

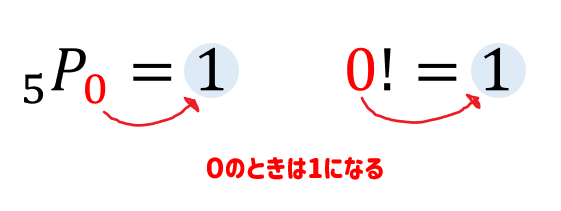
0がでてきたときには1になります。

これはそういうもんだってことで覚えておいてくださいな！

では、次の問題の答えも簡単に求まりますね。

ともに0が含まれているので、計算をすることなく答えが1だと分かります。

$${}_6 \mathrm{ P }_0=1\cdots(解)$$

$$0!=1\cdots(解)$$

nが含まれている順列Pの計算

げっ…\(n\)が入ってるけど、どーすんの！？

となってしまいますが、基本通りに考えてみましょう。

\({}_n \mathrm{ P }_3\)というのは

\(n\)からスタートして、1つずつ数を減らしながら3回かけ算する

っていう意味だよね。

ちなみに、\(n\)から1つ数を減らすと\(n-1\)。

さらに1つ数を減らすと\(n-1-1=n-2\)となりますね。

これを利用すると

$$\begin{eqnarray}{}_n \mathrm{ P }_3=n(n-1)(n-2)\cdots(解) \end{eqnarray}$$

となります。

これは展開せずに答えとする場合が多いので、このままの形でOKです。

と、まぁ\(n\)という文字にまどわされず

基本通りに式を作っていけばOKです。

練習問題に挑戦

では、順列Pの計算についての理解が深まっているかどうか練習問題に挑戦してみましょう！

順列Pの意味とは、どんな場面で使うの？

さて、ここまでは順列Pの計算方法について解説をしてきました。

計算はできるようになったとはいえ

どういった場面で使えるのかを理解しておかないと意味がありませんね。

というわけで、順列Pの意味についてサクッと解説しておきます。

\({}_5 \mathrm{ P }_3\)というのは

「5個から3個を取り出して並べる方法は何通りあるか」

を表しているものになります。

そして、上で紹介してきた計算方法によって

これが何通りあるのかを計算することができるというわけです。

7個から4個を取り出して並べるのは何通りある？

っていうのは、Pを使って表すと\({}_7 \mathrm{ P }_4\)となります。

文章で書くと長いけど、Pを使って表すとスッキリと短く表せますね。

そういった意味でPはとても便利な記号ってわけです。

では、順列Pを用いる文章題をちょっとだけ確認しておきましょう。

「8人の中から3人を選んで並べる」

ということだから、Pを使うと\({}_8 \mathrm{ P }_3\)となりますね。

あとは計算あるのみです。

$${}_8 \mathrm{ P }_3=8\cdot7\cdot6=336通り\cdots(解)$$

「5人の中から5人全員を並べる」

\({}_5 \mathrm{ P }_5\)だから、階乗を用いて\(5!\)ということになりますね。

$$5!=5\cdot4\cdot3\cdot2\cdot1=120通り\cdots(解)$$

まとめ！

お疲れ様でした！

これで順列Pの計算方法についてはバッチリかな？

順列Pの計算はいろんな場面で活躍します。

たくさん練習して、スラスラと計算できるようにしておきましょう。

ファイトだ(/・ω・)/

Pの計算がバッチリになったら、次は組み合わせCの計算だね！

⇒ 組み合わせCの計算のやり方を簡単にサクッと解説するぞ！