今回は約数の積を素因数分解で表すやり方について解説します。
【問題】
(1)200のすべての正の約数の積を素因数分解して表しなさい。
(2)144のすべての正の約数の積を素因数分解して表しなさい。
「約数の個数」「約数の総和」については、こちらの記事でも解説していますが
約数の積ってどうやるの!?って感じですよね(^^;)
なので、どういった考え方で解いていけばよいのかイチから順に解説していきますね。
今回の内容をサクッと理解したい方はこちらの動画がおススメです^^
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
約数の積の考え方
いきなり200、144といった大きな数を扱うと難しく感じちゃうので、まずは20という小さい数を例にあげて考えてみましょう。
【例題】
20のすべての正の約数の積を素因数分解して表しなさい。
20の約数は「1,2,4,5,10,20」の6個ですね。
これらを全部かけた式をつくって、両端からペアをつくっていくと、20が全部で3個できるってことが分かります。
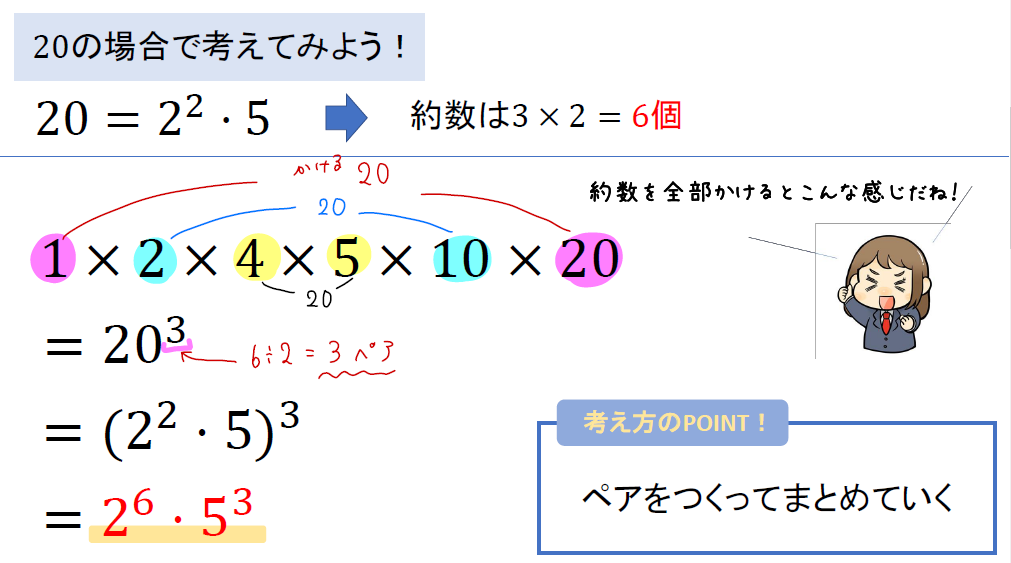
このように約数の両端からペアを作ってまとめていくことで、工夫しながら素因数分解の形に変形していくようになります。
これが約数の積を表すときのコツになります!
では、このコツを利用しながらそれぞれの問題にチャレンジしてみましょう。
(1)の解説~偶数個~
【問題】
(1)200のすべての正の約数の積を素因数分解して表しなさい。

答え
$$2^{18}\cdot 5^{12}$$
まずは素因数分解して、約数の個数を求める。
今回は12個なので、200が6ペア作れることがわかりますね。
そこから\(200^6\)を作って変形していけばOKです。
(2)の解説~奇数個~
【問題】
(2)144のすべての正の約数の積を素因数分解して表しなさい。
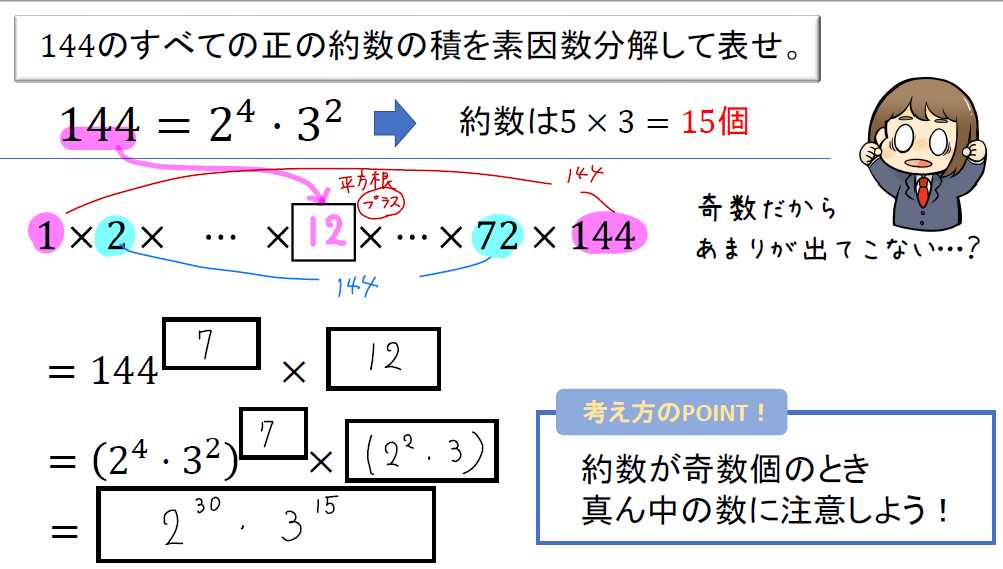
答え
$$2^{30}\cdot 3^{15}$$
約数が奇数個になるときはちょっと注意!
約数を並べたとき、ちょうど真ん中の数がペアにならず余ってしまいます。
(真ん中には元の平方数がきます)
ですので、今回であれば「144が7ペア、12があまり」といった感じになります。
そこから、\(144^7\times 12\) という式をつくって、あとは変形していけばOK!
約数が奇数個になるときは、ペアにならず余ってしまうものがあるので注意ですね!
まとめ
というわけで、今回は約数の積についてサクッと解説しました。
これはやり方を知ってるかどうかが大事な問題です。
今回の記事を通して「ペアを作ればいいんだ!」という知識を手に入れてもらえれば、大きな成長だと思うので僕としては満足です^^
お疲れ様でした(‘ω’)ノ














コメントを残す