集合の要素の個数の最大・最小を求める！イメージ図と不等式を使って考える！

高校数学Ａで学習する集合の単元から

「集合の要素の個数の最大・最小を求める」

について解説していきます。

集合の要素の個数を考える基礎問題は

こちらで解説してるのでご参考くださいね！

さて、今回取り上げる問題はこちら！

最大値、最小値！？

なんだか難しそう…と思うかもしれませんが、

結構、楽勝な問題です(/・ω・)/

イメージ図と不等式を使ってサクッと解けるようにしておきましょう。

今回の内容はこちらの動画でも解説しています！

動画なら手短にサクッと理解できますよ＾＾

\(n(A\cap B)\) の最大値と最小値

\(n(A\cap B)\) というのは、ＡとＢの重なっている部分のこと。

そして、この重なっている部分が最大になるというのは…

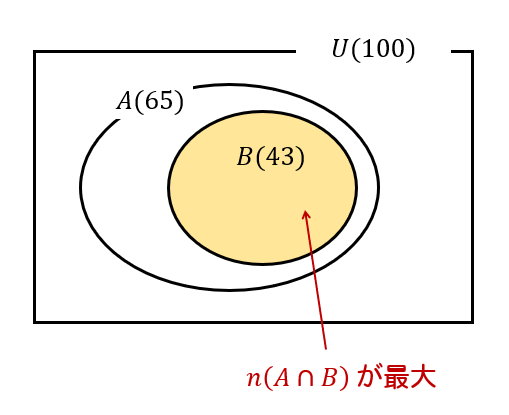
このように、小さい方が大きい方にすっぽりと入っているとき。

かっこよく数式で表すなら、\(A\supset B\) のときですね。

$$\begin{eqnarray}n(A\cap B)&=&n(B)\\[5pt]&=&43\cdots (解) \end{eqnarray}$$

よって、最大は43となります。

最大は小さい方が大きい方にすっぽり入るとき。

つまり、小さい集合の個数と一致するってことになります。

めっちゃ簡単ですね(/・ω・)/

次に最小値を考えてみましょう。

「ＡとＢがなるべく重ならないようにする」ってことですね。

イメージとしては、Ｕという箱の両端からＡとＢを並べていく感じです。

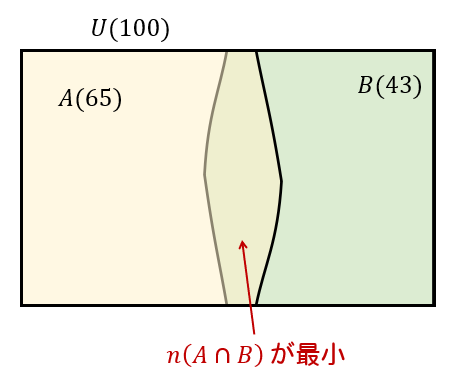
すると、このように真ん中で仕方なく重なっちゃう部分がでてきます。

どれくらいの数が重なってしまうかというと、

AとBの個数を足すと、\(65+43=108\) となり、\(U\) が100の箱なので、8だけ溢れてしまうことが分かります。

つまり、なるべく重ならないように並べていってもどうしても「8」だけは重なってしまうということです。

これが \(A\cap B\) の最小値ですね。

もうちょっと数学っぽく式で表すなら次のようになります。

$$\begin{eqnarray}n(A\cap B)&=&n(A)+n(B)-n(U)\\[5pt]&=&65+43-100\\[5pt]&=&8\cdots(解) \end{eqnarray}$$

ポイント！

• 最大を考えるときは、小さい方が大きい方にすっぽり入るイメージ

• 最小を考えるときは、それぞれの集合を重ならないように並べたときに仕方なく重なってしまうのはどれくらいかを考える。

不等式を使ってかっこよく求める方法

前の章ではイメージ図を使って考えてもらいましたが、

次は、不等式を使ってかっこよくスマートに求める方法も紹介しておきます。

集合の要素の個数は、次のような不等式が成り立ちます。

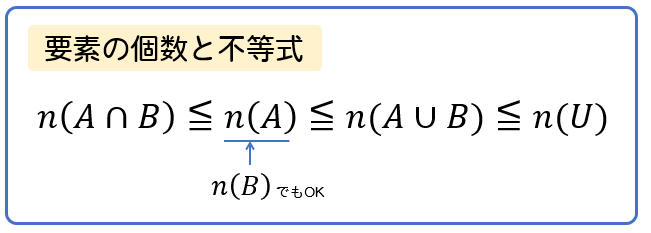
難しそうな式に見えますが、落ち着いて考えてもらえれば

あぁ、そりゃそうだよな。

って思ってもらえると思います。

そして、この不等式を使って \(n(A\cap B)\) の最大・最小を考えてみます。

\(n(A\cap B) =x\) とすると、

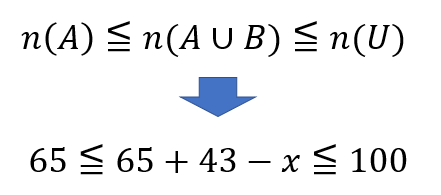
$$\begin{eqnarray}65&≦&108-x≦100\\[5pt]-43&≦&-x≦-8\\[5pt]8&≦&x≦43 \end{eqnarray}$$

このように最大・最小を求めることができます。

ちなみに、\(n(A)≧n(B)\) であることから左端の値には \(n(A)\) を採用しています。

ここは大きい方の個数を当てはめるようにしてください。

不等式を使いこなせると、かなりスマートに計算することができますね！

また、次に紹介する（2）のような問題でも不等式は活躍します。

\(n(\overline{A}\cap B)\) の最大値と最小値

まずは、\(\overline{A}\cap B\) がどこの部分を表しているのか確認しておきましょう。

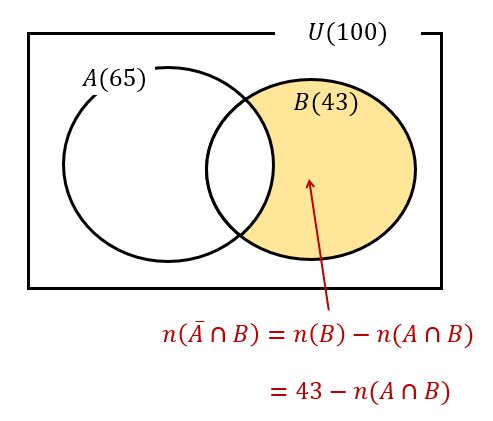
上の画像のように、Bの集合からAとBの共通部分を取り除いた部分のことですね。

つまり、\(n(\overline{A}\cap B)=n(B)-n(A\cap B)=43-n(A\cap B)\) となります。

では、これの最大・最小はどうやって考えていけばよいのでしょうか。

これは、（1）で \(n(A\cap B)\) の最大・最小を求めている場合には楽勝な話です！

\(n(\overline{A}\cap B)\) は、43から \(n(A\cap B)\) を引いた値です。

ってことは、 \(n(A\cap B)\)が最大のときに\(n(\overline{A}\cap B)\) は最小となる。

そして、\(n(A\cap B)\)が最小のときに\(n(\overline{A}\cap B)\) は最大となるってことです。

というわけなので、（1）より

\(n(\overline{A}\cap B)=43-43=0\)

\(n(\overline{A}\cap B)=43-8=35\)

個人的には、不等式を使って最大・最小を求める方法も好きです。

ぜひ、こちらのやり方も覚えておいてくださいな！

不等式で求めたほうが何だかスッキリするというか…

数学っぽくてカッコいいですよねｗ

【練習問題】集合の要素の個数の最大・最小

まとめ！

お疲れ様でした！

集合の要素の個数の最大・最小について理解してもらえましたでしょうか？

基本問題に関しては、しっかりとイメージ図を利用して考えていくことが大事ですね。

また、不等式を使った考え方も理解しておけると、

いろんな問題に対応できるようになって便利ですよ(/・ω・)/

たくさん練習問題を解いて、理解を深めておいてくださいね！