【反復試行の確率】なぜこんな公式になるの？Cを使う理由は？

今回は数学Aで学習する確率の単元から

『反復試行の確率公式』

について学習していきましょう。

反復試行の確率を苦手としている人は多い！

なぜなら公式が難しく見えちゃうから…だね(^^;)

だけど、ちゃんと意味を理解して公式を覚えることができれば

あれ、簡単じゃね！

となるはずです。

今回はそんな反復試行の公式の考え方を１から見ていきましょう。

今回の内容はこちらの動画でも解説しています！

Contents

反復試行の公式
- 公式のなぜ
公式にCを使う理由
練習問題に挑戦！
まとめ
がんばっているのに60点の壁をクリアできない中3生の方へ
- こちらの関連記事はいかがでしょうか？

反復試行の公式

反復試行の公式
1回の施行で事象Aの起こる確率が$p$で、この試行を$n$回繰り返し行うとき、Aがちょうど$r$回起こる確率は
$$\large{{}_n \mathrm{ C }_rp^rq^{n-r}}$$

んーーーー難しいｗ

記号が多すぎて、何を言ってるのか分からんですね(^^;)

なので、この公式の意味を1つずつかみ砕いていきましょう。

それでは次の問題を取り上げて反復試行の考え方について触れていきます。

公式のなぜ

1個のさいころを3回投げるとき、3の目がちょうど2回出る確率を求めよ。

さいころを投げて3の目が出る確率は$\displaystyle{\frac{1}{6}}$であり、3の目以外が出る確率は$\displaystyle{\frac{5}{6}}$となりますね。

更に、さいころを3回投げて3の目がちょうど2回出るというのは次のようなパターンが考えられます。

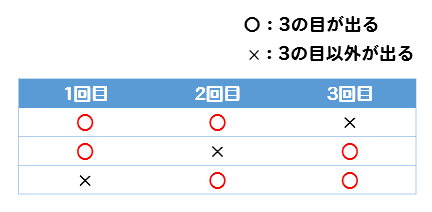
1回目と2回目に出るパターン

1回目と3回目に出るパターン

2回目と3回目に出るパターンの3つが考えられます。

それでは、それぞれのパターンにおいて確率を求めていきましょう。

1回目と2回目に3の目が出る確率は

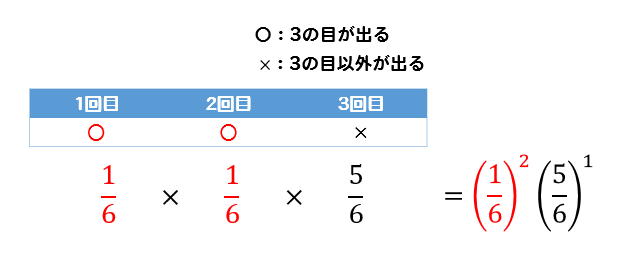
同様に他のパターンも考えると

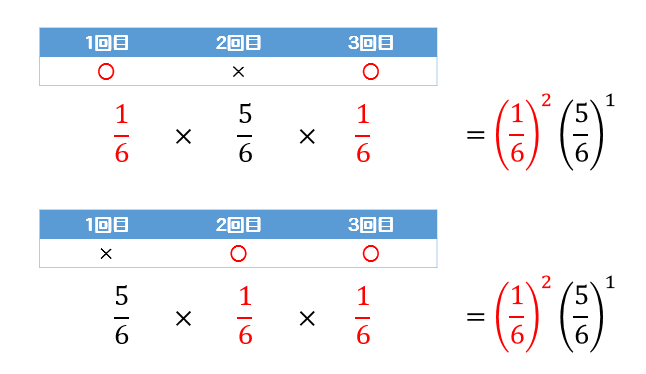
このようになりました。

これらの確率を合計すれば、答えが求まるわけなんですが…

何か気付いたことがありますよね？

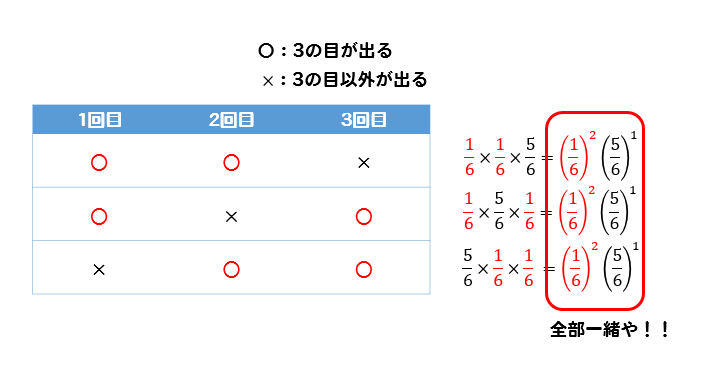
ぜんぶ一緒やんけ！！

ということです。

そうなんです。

反復試行の場合、考えなければいけないパターンはたくさんあるのですが、それぞれのパターンにおいての確率は全部同じになってしまうんですね。

だったら…

1パターンの確率を求めてしまって、あとはそれが何パターンあるのかを計算すればOK！ということになります。

これで、だいぶ楽に計算ができるようになりますね。

更に…

今回は全部で3パターンだということが簡単に分かったけど、これを手作業で数えるのってめんどくね？ってなるわけです。

どうせなら、ここも簡単に計算ができると嬉しいですよね。

そこで出てくるのが、Cです。

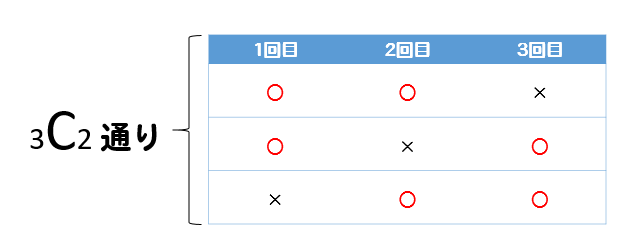
3回中、2回〇になるのが何通りあるか求めたいので

$${}_3 \mathrm{ C }_2=\frac{3\cdot 2}{2\cdot 1}=3$$

を計算することによって、3通りあることがすぐにわかります。

よって、この問題の反復試行はこのように解くことができました。

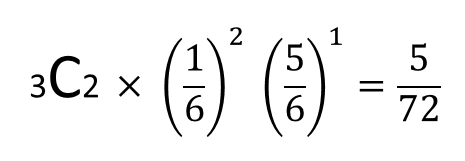
このような考え方をまとめたものが、反復試行の公式になります。

まず、Cを使って何通りのパターンがあるかを求める。

それぞれが何回ずつ出るかを考え確率を求める。

その確率が何通りあるのかを掛け算すれば完成！

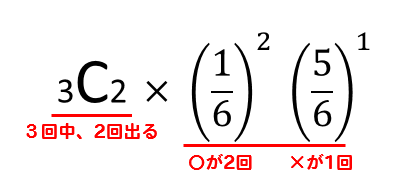
まぁ、そんなに難しいことじゃないよね！

公式にCを使う理由

公式の中にCが出てくる理由は分かりましたか？

ここで出てくるCというのは、反復試行で考えられるパターンが何通りかを計算している部分でしたね。

何回中、何回〇が出てくるのかを考えるのだから

7回中、3回〇が出るという場合には

$$\large{{}_7 \mathrm{ C }_3}$$

9回中、2回〇が出るという場合には

$$\large{{}_9 \mathrm{ C }_2}$$

というようにそれぞれのパターンを計算で求めることができます。

だから、公式の中にCが出てくるのですね！

練習問題に挑戦！

それでは、反復試行の公式を使って練習問題に挑戦してみましょう。

1個のさいころを3回投げるとき、偶数の目が1回出るときの確率を求めよ。

解説＆答えはこちら

答え

$$\frac{3}{8}$$

まず、偶数の目が出る確率は$\displaystyle{\frac{1}{2}}$であり、偶数が出ない（奇数が出る）確率は$\displaystyle{\frac{1}{2}}$となります。

これを用いて考えると

$${}_3 \mathrm{ C }_1\left(\frac{1}{2}\right)^1\left(\frac{1}{2}\right)^2$$

$$=3\times \frac{1}{2}\times \frac{1}{4}$$

$$=\frac{3}{8}$$

2個の赤玉、1個の白玉が入っている袋から玉を1個取り出し、色を調べてから元に戻すことを5回行うとき、ちょうど4回赤玉が出る確率を求めよ。

解説＆答えはこちら

答え

$$\frac{80}{243}$$

まず、赤玉が出る確率は$\displaystyle{\frac{2}{3}}$であり、赤玉が出ない（白玉が出る）確率は$\displaystyle{\frac{1}{3}}$となります。

これを用いて考えると

$${}_5 \mathrm{ C }_4\left(\frac{2}{3}\right)^4\left(\frac{1}{3}\right)^1$$

$$=5\times \frac{16}{81}\times \frac{1}{3}$$

$$=\frac{80}{243}$$

1枚の硬貨を7回投げるとき、6回以上表が出る確率を求めよ。

解説＆答えはこちら

答え

$$\frac{1}{16}$$

まず、表が出る確率は$\displaystyle{\frac{1}{2}}$であり、表が出ない（裏が出る）確率は$\displaystyle{\frac{1}{2}}$となります。

表が6回以上出るときを問われているので

表が6回出るとき、7回出るときをそれぞれ考える必要があります。

表がちょうど6回出るときの確率は

$${}_7 \mathrm{ C }_6\left(\frac{1}{2}\right)^6\left(\frac{1}{2}\right)^1$$

$$=7\times \frac{1}{64}\times \frac{1}{2}$$

$$=\frac{7}{128}$$

表がちょうど7回出るときの確率は

$${}_7 \mathrm{ C }_7\left(\frac{1}{2}\right)^7$$

$$=1\times \frac{1}{128}$$

$$=\frac{1}{128}$$

以上より

$$\frac{7}{128}+\frac{1}{128}=\frac{8}{128}=\frac{1}{16}$$

まとめ

お疲れ様でした！

反復試行の公式は、見た目が難しいんだけど

その理由について知れば、別に難しいものではありませんでしたね。

Cを使って何通りか求める。

それぞれが何回ずつ出るかから確率を出す。

それらを掛ける！

以上！！

しっかりとやり方を覚えておきましょう(/・ω・)/

こちらの記事も合わせてどうぞ！

がんばっているのに60点の壁をクリアできない中3生の方へ

頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。

もしかして、
このような問題に直面していませんか？

模試になると点がガクッと落ちる
復習のやり方が分からない
勉強してもすぐに忘れる
凡ミスが直らない
家だと集中して勉強できない
問題集を買っても、1人で解けなくて途中でやめてしまう
友人が点を伸ばしていて焦る
頑張りたいから何をすればいいか教えて欲しい

僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。

すごく勉強したのに試験の結果が36点…

「どうすればいいか分からない…」
「点を上げれる自信がない…」

自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！

なんと、たった2ヶ月で
36点　⇒　72点
なんと、驚きの36点UPを達成！

何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。

この勉強法を活用した人は、

43点　⇒　69点

67点　⇒　94点

人生初の100点！

このように次々と良い結果を報告してくれています＾＾

Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。

そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。

こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！

もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ

無料でワークをもらう！

数スタの他記事はこちらから