100～200までの整数のうち、次の整数の個数を求めよ。
（1）5の倍数
（2）5の倍数でない
（3）7の倍数
（4）5かつ7の倍数
（5）5または7の倍数
（6）5の倍数であるが7の倍数でない
このように倍数の個数について問われる問題。
どのように考えていけばよいのでしょうか。
この問題は算数、高校数学の両方で学習する内容です。
どちらの方にも理解できるように1問ずつていねいに解説していきますね(^^)
Contents
倍数の個数を考える
（1）～（3）倍数の数え方
100～200までの整数のうち、次の整数の個数を求めよ。
（1）5の倍数
100～200までの間には、どんな5の倍数があるのか考えてみると…
$$\{100,105,110,\cdots,200\}$$
という数が入っていることが分かります。
でも、これっていくつあるのかが分かりにくいです。
なので、次のように掛け算の形にして表してみると分かりやすくなります。
$$\{5\times 20,5\times 21,\cdots,5\times 40\}$$
すると、\(5\times 20\)からスタートして\(5\times 40\)まであるということが読み取れます。
つまり
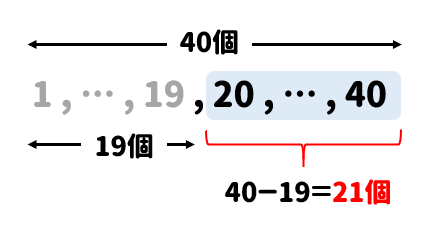
こんな感じで考えて
$$40-19=21個$$
となります。
よくある間違いで、\(40-20=20個\)としてしまう人がいます。
これだと1個多く数えてしまっているので、
上の画像のように1～40の中から20の手前である1から19を取り除いたと考えるようにしてください。
（1）答え
$$21個$$
100～200までの整数のうち、次の整数の個数を求めよ。
（2）5の倍数でない
100～200までの中には、\(200-99=101個\)の整数が入っています。
この中に5の倍数は（1）より21個ありましたね。
つまり、5の倍数でない整数は
$$101-21=80個$$
となります。
「～でない」という場合には、全体の個数から「～である」を引いてあげればOKです。
（2）答え
$$80個$$
100～200までの整数のうち、次の整数の個数を求めよ。
（3）7の倍数
（1）と同様に考えてみましょう。
$$\begin{eqnarray}&&\{105,112,\cdots ,196\}\\[5pt]&=&\{7\times 15, 7\times 16,\cdots ,7\times 28\} \end{eqnarray}$$
よって、7の倍数は
$$28-14=14個$$
となります。
（3）答え
$$14個$$
（4）「かつ」の考え方
100～200までの整数のうち、次の整数の個数を求めよ。
（4）5かつ7の倍数
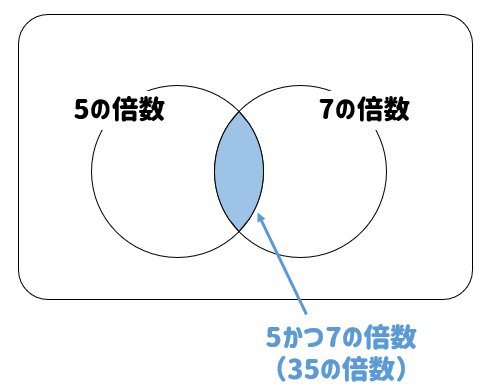
「かつ」の場合には最小公倍数を考えることになります。
今回の問題では、「5かつ7の倍数 ⇔ 35の倍数」となります。
図で書くと、2つが重なっている部分ってことですね。
$$\begin{eqnarray}&&\{105,140,175\}\\[5pt]&=&\{7\times 15, 7\times 16,7\times 17\} \end{eqnarray}$$
よって、35の倍数（5かつ7の倍数）は
$$17-14=3個$$
となります。
まぁ、これくらいの数であれば目で数えたほうが早いですね(^^;)
（4）答え
$$3個$$
（5）「または」の考え方
100～200までの整数のうち、次の整数の個数を求めよ。
（5）5または7の倍数
「または」の場合には次のように考えましょう。
（5の倍数）＋（7の倍数）－（5かつ7の倍数）
図で書くと分かりやすいです。
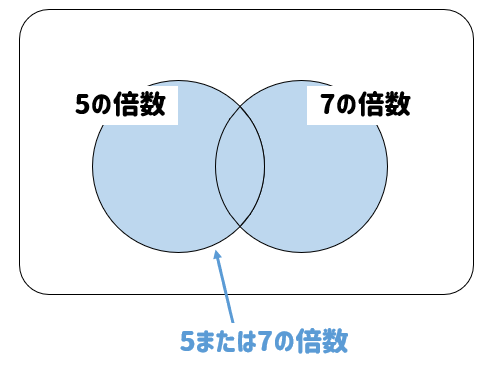
「または」というのは色がついているすべての部分のことを表しています。
なので、5の倍数と7の倍数の個数を足し合わせます。
しかし、そのまま足してしまうと重なっている部分がダブってしまいます。
なので、ダブったところを取り除くために「かつ」の部分を引いてあげるのです。
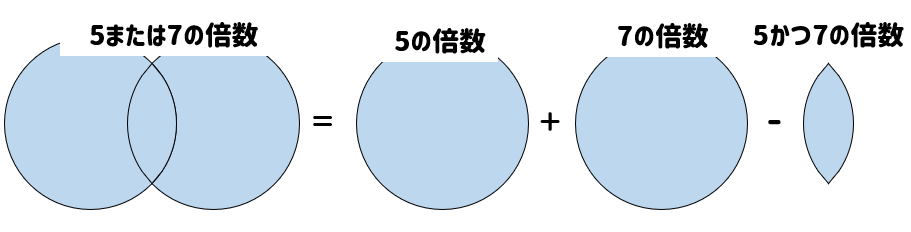
（1）（3）（4）の答えを利用すると
$$21+14-3=32個$$
となります。
（5）答え
$$32個$$
（6）「～ではあるが～ではない」の考え方
100～200までの整数のうち、次の整数の個数を求めよ。
（6）5の倍数であるが7の倍数でない
これは少しややこしい表現ではありますが
「5の倍数の中から7の倍数を取り除いたもの」
ってことになります。
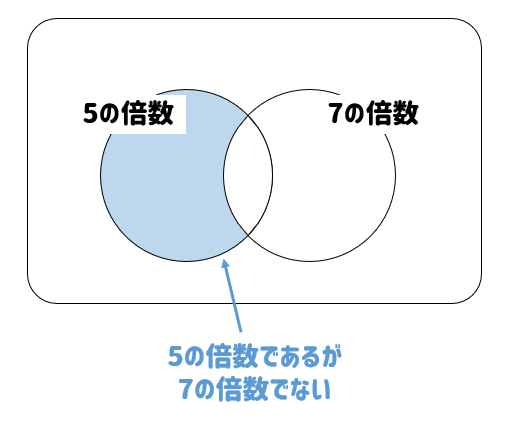
つまり、5の倍数から35の倍数を引いてあげればOKということになります。
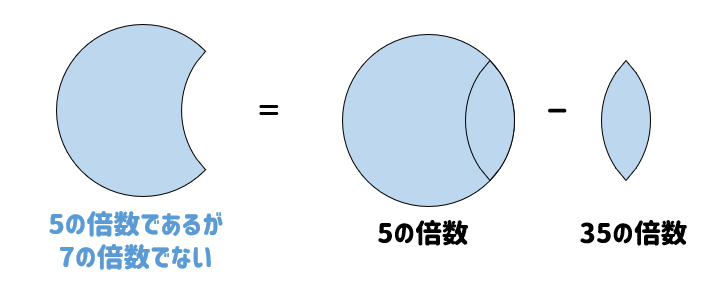
よって、（1）（3）より
$$21-3=18個$$
（6）答え
$$18個$$
まとめ！
今回は倍数の数え方についてパターン別に解説しました。
（1）で解説したように、個数の数え方には注意です。
20～40を数えるというときには、
「1～40」引く「1～19」というイメージを持っておきましょう。
「または」「～であるが～でない」など
ややこしい言い回しが出てきた場合には図を書いて考えてみるとよいですね。
問われている部分がどこなのか、色をつけて考えると分かりやすくなります(/・ω・)/
高校入試で使える公式集をプレゼント！
高校入試で使える公式をまとめた教材を作成しました！
定期テスト、入試で高得点を取るためには絶対に知っておきたいものばかりを集めています。
学校では教えてくれないような公式もありますよ(/・ω・)/
これは知らないと損をするかも…！？
無料の中学生メルマガ講座にご登録いただいた方に、
高校入試で使える公式集をプレゼントさせていただいております。
こちらから公式集を無料で手に入れちゃってください！
ご登録いただいたメールアドレスに教材を送らせていただきます。
登録は1分もあれば完了します。
ぜひ、こちらから中学生メルマガ講座に登録してみてくださいね(^^)
コメントを残す