【数学A】集合の要素の個数の問題「できた・できない・どちらも～」

高校数学Aで学習する集合の単元から

「集合の要素の個数を求める問題」

について解説していきます。

取り上げる問題はこちら！

この問題を解くためには、イメージを書いておくのが大事です！

倍数の個数を求める問題はこちらで解説しています。

>倍数の個数を求める問題、どうやって考えればいい？？

ぜひ、ご参考ください(^^)

今回の問題はこちらの動画でも解説しています。

サクッと効率よく身につけたいなら動画がおススメです！

集合の要素の個数（1）の解説！

まずは、問題の情報を元にイメージ図をかいてみましょう！

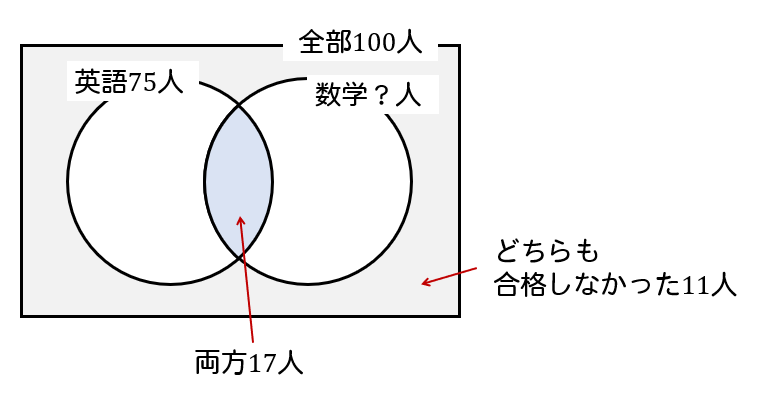
そして、「少なくとも1教科に合格した生徒」というのは、

「英語に合格」または「数学に合格」のどちらか、または両方の生徒のことなので

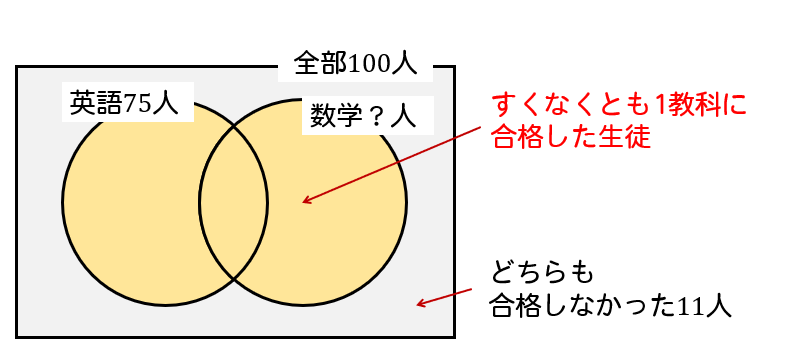
ここの部分だってことが分かりますね。

これが分かれば、人数を求めるのは簡単！

全体の人数から「どちらにも合格しなかった」人数をを引けば求めることができますね。

よって、\(100-11=89\)人となります。

もうちょっと数学っぽく、式を用いて計算するなら次のように書くことができます。

式で書こうとするとちょっと難しく見えますね(^^;)

まぁ、イメージを書いて、図から個数を読み取れるのであれば大丈夫だと思います！

集合の要素の個数（2）の解説！

数学の試験に合格した生徒は、

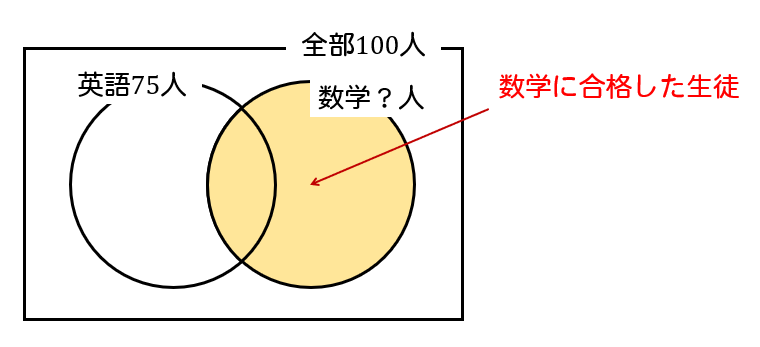
ここの部分のことですね。

（1）より、円2つの中には全部で89人の生徒がいると分かっています。

ですので、次の式に当てはめていけば数学の合格者数を求めることができます。

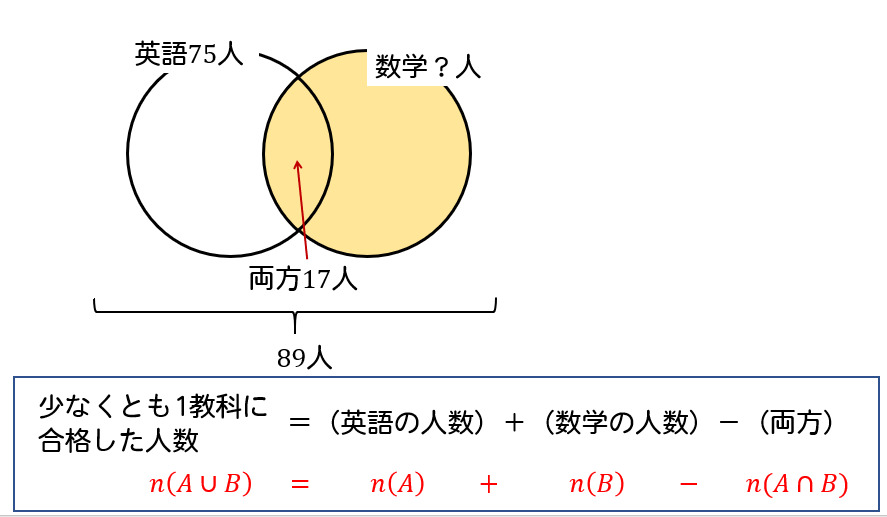
$$\begin{eqnarray}89&=&75+n(B)-17\\[5pt]n(B)&=&89-75+17\\[5pt]&=&31人 \end{eqnarray}$$

和集合の要素の個数が絡んでくるときには、

\(n(A\cup B)=n(A)+n(B)-n(A\cap B)\) の形を利用していくようになるので、

これは絶対に覚えておいてくださいね！

集合の要素の個数【練習問題】

まとめ！

お疲れ様でした！

集合の要素の個数を考えるときには、イメージ図を利用するのが一番です。

数式で計算式を作ると、ちょっと難しく見えちゃうんもんね(^^;)

まぁ、慣れてくれば数式を利用した方が計算が速くなりますので、

まずはたくさん練習問題をこなしていきましょう！