【じゅず順列】問題の解き方はどうやる？円順列との違いは？

今回は高校数学Aで学習する場合の数の単元から「じゅず順列」についてイチから解説します！

取り上げる問題はこちら！

円順列との違いについて理解しながら進めていきましょう＾＾

今回の内容はこちらの動画でも解説しています！

じゅず順列と円順列の違い

円順列とは回転させたときに一致するものを1通りとして数える順列のことでしたね。

これに対して、じゅず順列とは回転させて一致するものに加え、ひっくり返したときに一致するものも1通りとして数える順列のことです。

首飾りのようなものをつくるときには席順とは異なり、そのもの自体をひっくり返すことができるので「じゅず順列」の考え方になります。

言葉だけでは伝わりにくいので…

具体例を見ながらそれぞれの違いをチェックしてみましょう。

例えば、4色の玉を並べるとき

円順列だと次のように6通りになります。

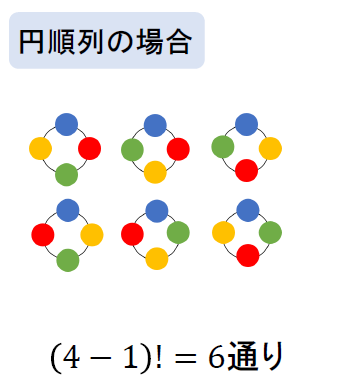
一方で、じゅず順列の場合

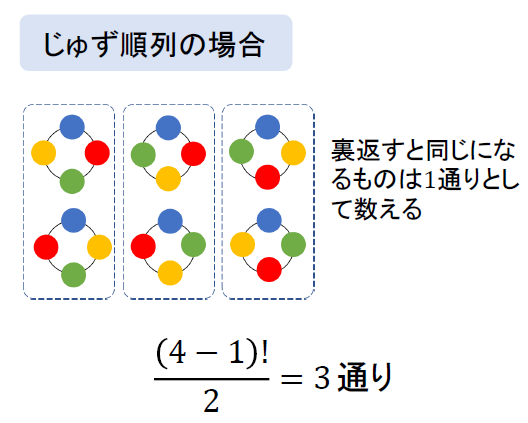
先ほど求めた円順列の中から、枠線で囲ったパターンはひっくり返すと一致させることができます。

これらをまとめて1通りとして数えるようになるので、総数は円順列の半分になってしまいます。

ちょっとかっこよくまとめておくとこんな感じです。

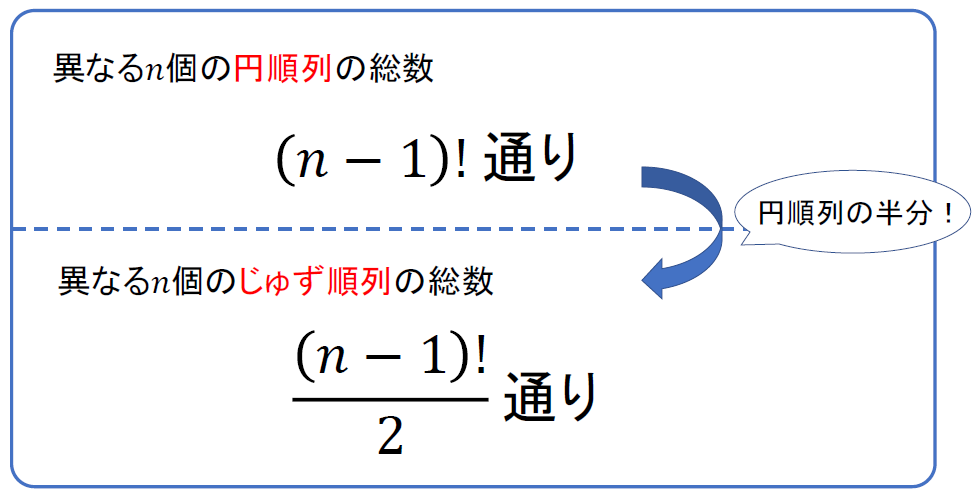
では、じゅず順列の特徴をおさえたところで、冒頭で紹介した問題を解いてみましょう。

5色の円順列を求めて、それを半分にすればいいので

$$\frac{(5-1)!}{2}=\frac{4\cdot 3\cdot 2\cdot 1}{2}=\color{red}{12通り}$$

簡単でしたね＾＾

では練習問題にチャレンジして今回の理解度を深めておきましょう。

練習問題にチャレンジ！

円順列なのか、じゅず順列なのか

よーく判断して解いてみましょう！

まとめ

お疲れ様でした！

じゅず順列について理解してもらえましたか？？

基本問題については「円順列の半分だ！」と覚えておけば大丈夫です＾＾

ただし…

今後もうちょっと難しいじゅず順列の問題も出てくるので、応用力を身につけたい方はこちらの記事もチェックしてみてください。

⇒ なぜ？同じものを含む順列の公式と使い方について問題解説！