一次関数と反比例の融合問題の解き方を解説！

今回は中2で学習する一次関数の単元から「一次関数と反比例の融合問題」について解説します。

取り上げる問題はこちら！

【問題①】

図のように、$y=\frac{a}{x}$のグラフと$y=4x+b$のグラフが2点P,Qで交わっている。$y=4x+b$のグラフと$x$軸との交点Rの$x$座標は$-1$、交点Rの$x$座標が$1$であるとき、$a$の値を求めなさい。

---

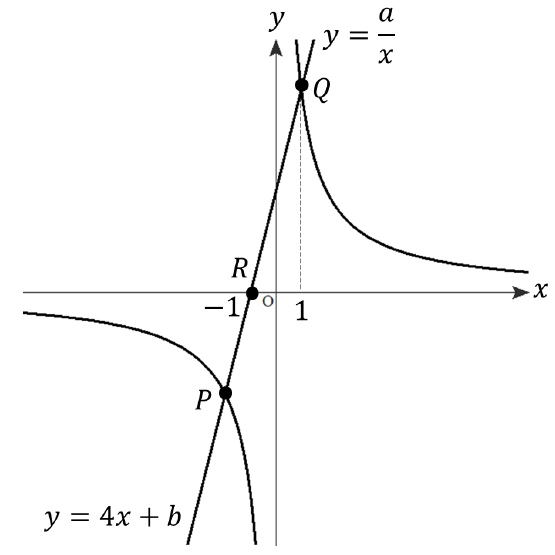
【問題②】

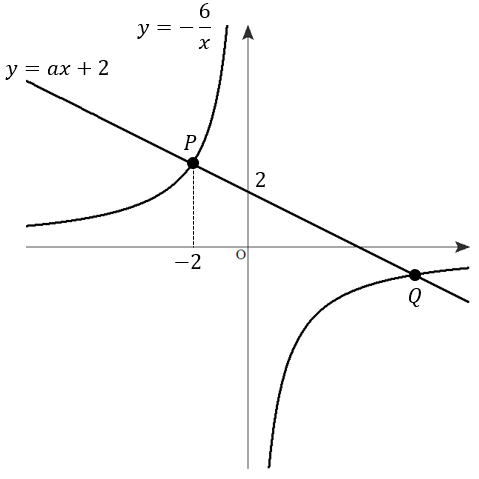
図のように、$y=-\frac{6}{x}$のグラフと直線$y=ax+2$が、2点P,Qで交わっている。Pの$x$座標が$-2$であるとき、$a$の値を求めなさい。

今回の問題はこちらの動画で解説しています！

【問題①】解き方をチェック！

図のように、$y=\frac{a}{x}$のグラフと$y=4x+b$のグラフが2点P,Qで交わっている。$y=4x+b$のグラフと$x$軸との交点Rの$x$座標は$-1$、交点Rの$x$座標が$1$であるとき、$a$の値を求めなさい。

P、Q、Rと3つの点がありますが、$x,y$座標がともにわかっている点R$(-1,0)$を活用して、$b$の値を求めにいきます！

点Rを通っている直線の式 $y=4x+b$ に$x=-1, y=0$を代入すると

$$\begin{eqnarray}0&=&-4+b\\[5pt]4&=&b \end{eqnarray}$$

このように$b$の値を求めることができます。

これによって直線の式が $y=4x+4$ と求まったので、次に点Qの座標を求めます。

$x=1$を直線の式に代入すると

$$\begin{eqnarray}y&=&4+4\\[5pt]y&=&8 \end{eqnarray}$$

よって、点Qの座標は$(1,8)$と求まります。

$y=\frac{a}{x}$のグラフ上にある点Qの座標（$x=1,y=8$）を式に代入すると

$$\begin{eqnarray}8&=&\frac{a}{1}\\[5pt]a&=&8 \end{eqnarray}$$

このように$a$の値が求まります。

座標を求める、座標を式に代入する

この2つを意識しながら、グラフを見てみると解法の糸口が見つかりますね！

【問題②】解き方をチェック！

図のように、$y=-\frac{6}{x}$のグラフと直線$y=ax+2$が、2点P,Qで交わっている。Pの$x$座標が$-2$であるとき、$a$の値を求めなさい。

まずは点Pの座標を求めましょう！

$x=-2$ を$y=-\frac{6}{x}$ に代入すると

$$\begin{eqnarray}y&=&-\frac{6}{-2}\\[5pt]y&=&3 \end{eqnarray}$$

よって、点Pの座標は$(-2,3)$ とわかります。

そして、この座標を直線の式$y=ax+2$に代入すると

$$\begin{eqnarray}3&=&-2a+2\\[5pt]1&=&-2a\\[5pt]a&=&-\frac{1}{2} \end{eqnarray}$$

このように$a$の値が求まります！

まとめ

お疲れ様でした！

直線と反比例が組み合わさると、見た目が複雑でイヤになっちゃいますね(^^;)

ですが、見るべきポイントが分かっていれば今回のように簡単に答えを出すことができます。

記事内でもお伝えしましたが、

座標を求める、座標を式に代入する

この意識を持っていれば自然と見るべきポイントが分かってくると思いますよ＾＾