【数学A】展開したときの項の数の求め方は？

答えの求め方は、とっても簡単！

\((a+b+c)\) の中には、\(a,b,c\) の3つ。

\((x+y)\) の中には、\(x,y\) の2つ。

よって、\(3\times 2=6個\cdots (解)\)  となります。

では、なぜこのような計算で展開したときの項数を求めることができるのでしょうか。

その考え方について解説していきます。

また、記事の最後にはちょっと難しい練習問題も用意しています。

そこで理解を深めておきましょう。

今回の内容はこちらの動画で(‘◇’)ゞもチェックできます(‘◇’)ゞ

展開したときの項の数の求め方

式の展開とは、次のように分配法則を使って計算するんでしたね。

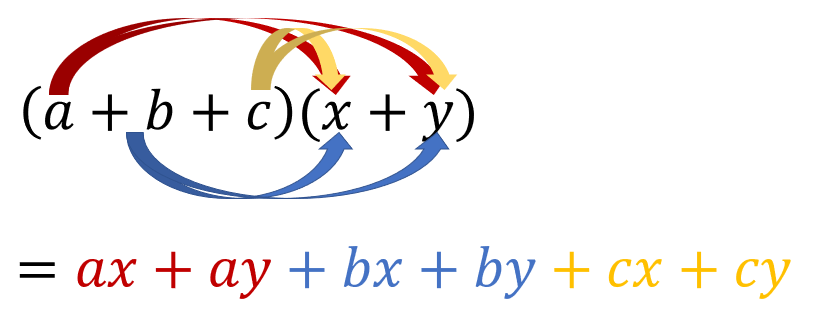
ってことは…

この分配法則の矢印の数だけ、項が出てくるってことになるよね。

展開したときに同類項が出てると、「矢印の数＝項数」とならなくなりますが、それは後ほど扱います。

では、矢印の個数はどのように考えればよいかというと

このように1つの項に対して、もう一方のカッコの中にある項の数だけ矢印ができるはずです。

となると、

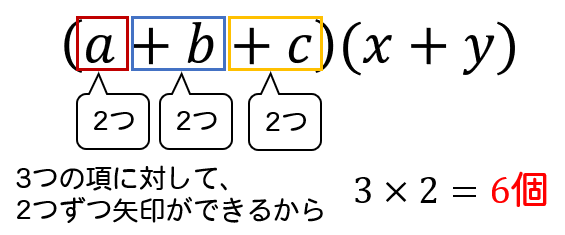
こんな感じで矢印の合計（項の数）を求めることができるってわけですね。

つまり、

カッコの中にある項の数をそれぞれ掛けると、展開したときの項の数を求めることができます。

これは、カッコが3つ以上になっても考え方は同じです。

ただし、次のような場合にはちょっと注意が必要です。

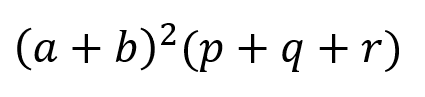
2乗だからこうすればいいんでしょー

って考えると罠にはまってしまいます(^^;)

2乗の部分は展開をすると同類項が出てくるので項数が3つになります。

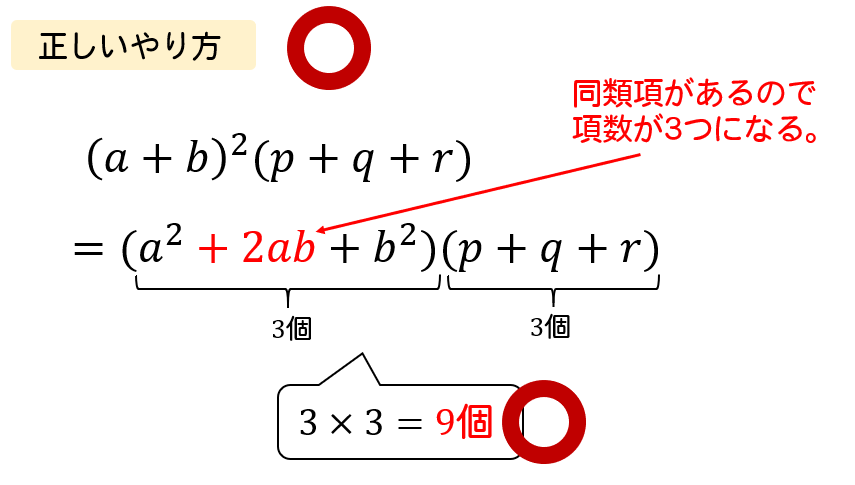
このように、2乗が出てきた場合には項数に気を付けて計算をしていくようにしましょう！

練習問題に挑戦！

まとめ！

お疲れ様でした！

これで展開したときの項の数についてはバッチリかな？

それぞれのカッコ内の項数をそれぞれ掛ければOK。

答えを求める計算については楽勝ですよね。

サクッと理解して、得点アップだ(/・ω・)/