【二次方程式の利用】花壇の道幅を求める文章問題を解説！

今回は、『二次方程式』の単元から

利用問題である道幅を考える問題に挑戦してみよう！

それでは、早速問題を見ていきましょう。

問題

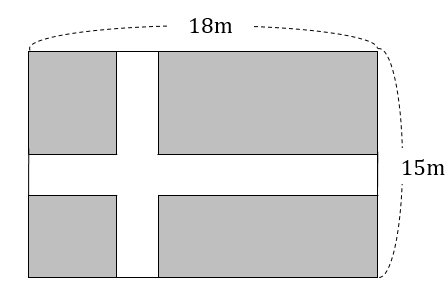
縦の長さが15m、横の長さが18mの長方形の土地があります。これに下の図のように、縦と横に同じ幅の道をつくり、残りを花壇にします。花壇の面積を180m²になるようにするには、道幅を何mにすればよいでしょうか。

今回の内容はこちらの動画でも解説しています。

サクッと理解したい方はこちらをどうぞ(‘◇’)ゞ

道幅の問題の考え方

んーーー

花壇の面積って言われても

花壇が4か所もあるから分かりにくい…

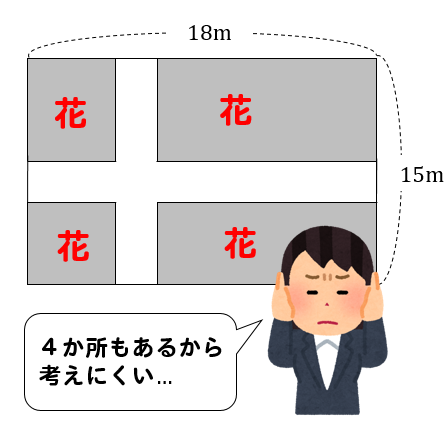
ってなっちゃうよね。

そういうときは、道を動かして

花壇を1か所に集めちゃおう！

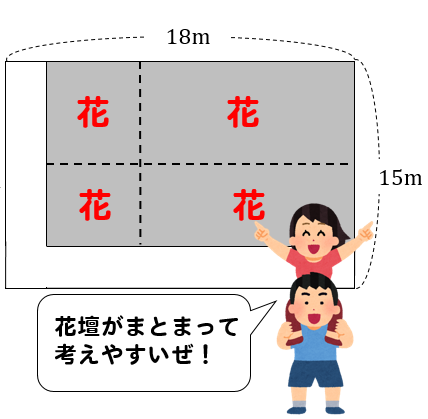
そうすることで

面積を考えやすくなるよね！

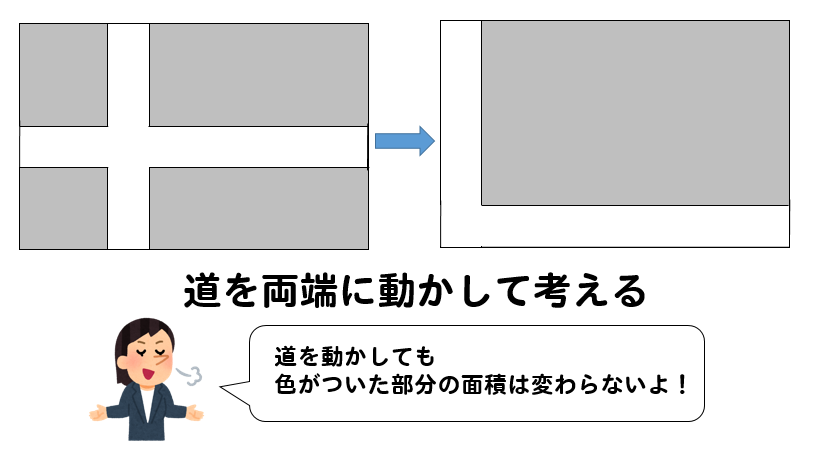
とういうことで

道幅を考えるような問題では

まず、道を両端に動かしてから面積を考えるようにしていきましょう。

道幅問題の解説！

それでは、今回の問題を考えていきます。

道幅を\(x\)mとすると

１つにまとまった花壇の横の長さは\((18-x)\)m、縦の長さは\((15-x)\)mと表すことができます。

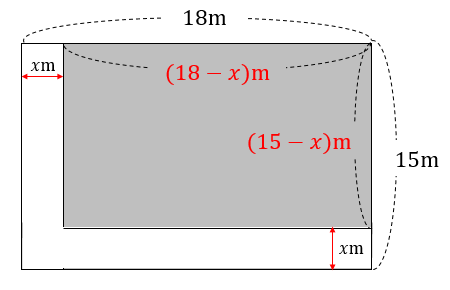
よって、花壇の面積は

$$(18-x)\times (15-x)$$

と表すことができます。

問題では、花壇の面積が180m²になるといっているので

$$(18-x)(15-x)=180$$

という方程式が作れます。

あとは、この方程式を解いていきましょう。

$$(18-x)(15-x)=180$$

$$270-33x+x^2=180$$

$$x^2-33x+90=0$$

$$(x-3)(x-30)=0$$

$$x=3,30$$

道幅は3mと30mだということが

方程式からわかりました。

でも、そもそもの土地が横18m、縦15mなのに

それよりも大きな30mの道幅なんて作れるはずがないよね。

ということで

方程式では3m、30mと2つの答えが出てきましたが

問題のシチュエーション的に30mの道幅はありえないから

今回の問題の答えは3mとなります。

二次方程式の文章問題では

このように問題のシチュエーションに合っているか確かめることが大切です！

道が2本に増えたらどうなる？？

それでは、今度はこちらの問題を見ていきましょう。

問題

縦8ｍ、横12mの長方形の土地があります。下の図のように、縦に2本、横に1本の同じ幅の道をつくり、残りの部分を花壇にします。花壇の面積と道の面積が同じになるようにするには、道の幅を何mにすればよいですか。

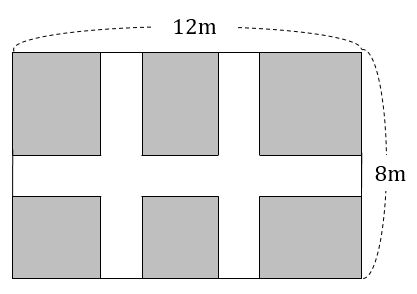
道が2本に増えたとしても、考え方は同じです。

全ての道を端に動かしましょう。

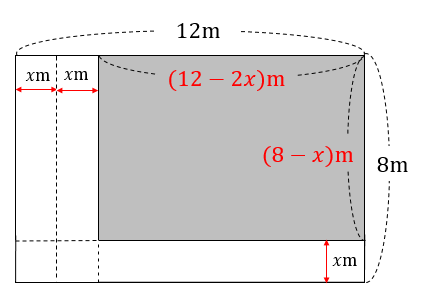
今回は、花壇の面積と道の面積が等しくなるということから

それぞれの面積を表していきましょう。

まず、花壇の面積は

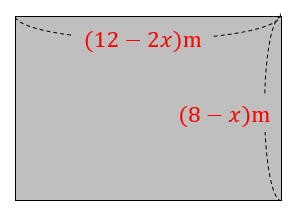
$$(12-2x)\times (8-x)$$

となります。

道の面積は

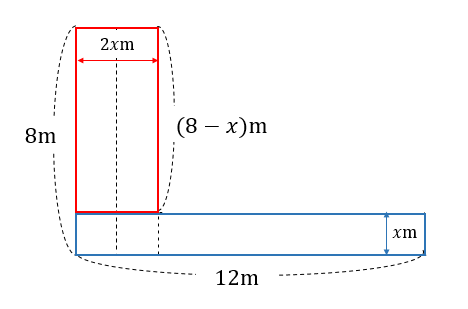
形が少し複雑なので、赤い図形と青い図形に分けて求めていきます。

まず、赤い図形の面積は

$$2x\times (8-x)$$

青い図形の面積は

$$12\times x$$

よって、道の面積は両方を足して

$$2x(8-x)+12x$$

と表すことができます。

花壇の面積と道の面積が等しくなることから

$$(12-2x)(8-x)=2x(8-x)+12x$$

となります。

あとは、この方程式を解いていきましょう。

$$(12-2x)(8-x)=2x(8-x)+12x$$

$$96-28x+2x^2=28x-2x^2$$

$$4x^2-56x+96=0$$

$$x^2-14x+24=0$$

$$(x-12)(x-2)=0$$

$$x=2,12$$

\(x=12\)は問題に合わないので

答えは2mとなります。

【追加演習】二次方程式の文章題をパターン別に攻略せよ！

今回は二次方程式の文章題特訓として、パターン別の演習課題を用意しました。

ここでは定期テストによく出題される「ある数、自然について」「図形」「箱の容積」「道幅」「動点」といった問題を取り上げています。これらが完璧に解けるようになれば、自信をもってテストに挑めるようになりますよ(‘ω’)ノ

動画解説も用意しているので、苦手な文章題も挫折することなく最後まで取り組めるはず！がんばってください＾＾

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

二次方程式　道幅の文章問題　まとめ

お疲れ様でした！

二次方程式の道幅の文章問題は

定期テストでよく出題されます。

見た目は難しそうですが

考え方はとっても簡単な問題です。

道を端に動かして考える！

これだけですね。

道が増えても、考え方は同じだからね！

たくさん練習して、必ず解けるようにしておきましょう。

ファイトだー(/・ω・)/