今回は中1数学で学習する
「図形の回転移動」
についてまとめておきます。
回転移動ってどんな移動?
回転移動の作図ってどうやるの?
回転移動したときに重ねられる図形はどれ?
これらの疑問に対して、1つずつ答えていきますね(^^)
回転移動の特徴
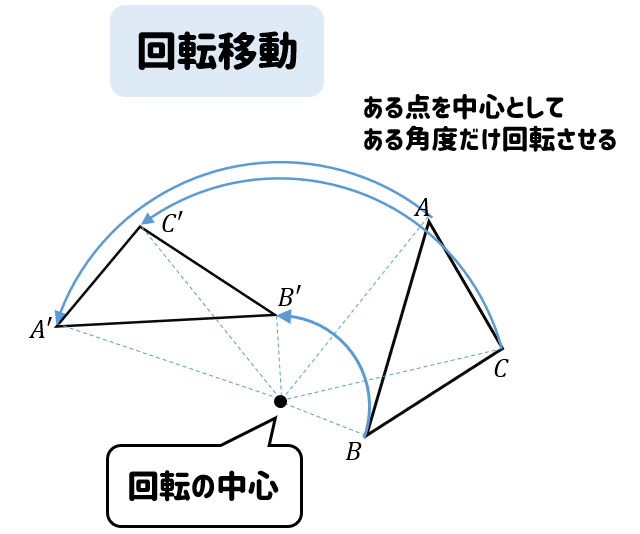
回転移動とは、ある点を中心として
ある角度だけ回転させる移動のことです。
このとき、中心としたある点のことを回転の中心といいます。
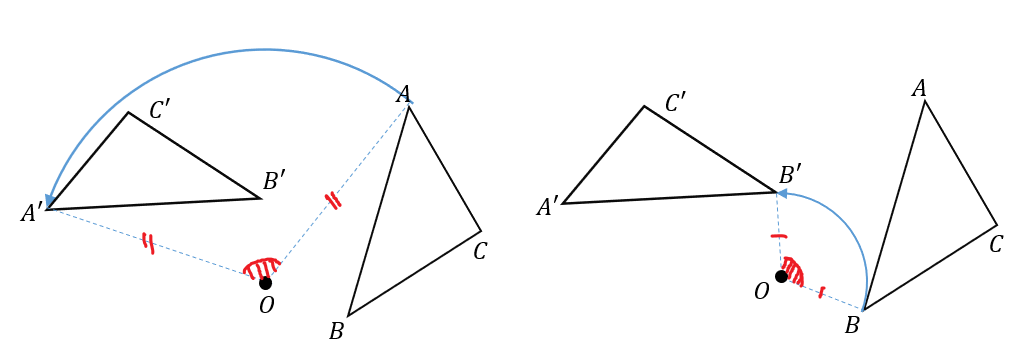
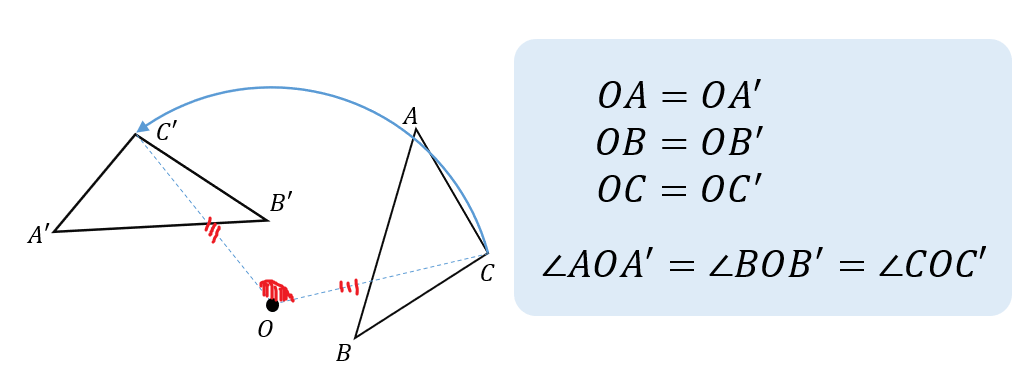
また、対応する頂点と回転の中心を結んだとき
それぞれの長さが等しくなり、なす角はすべて同じになります。
回転移動の中でも
180°に回転させるときには点対称移動といいます。
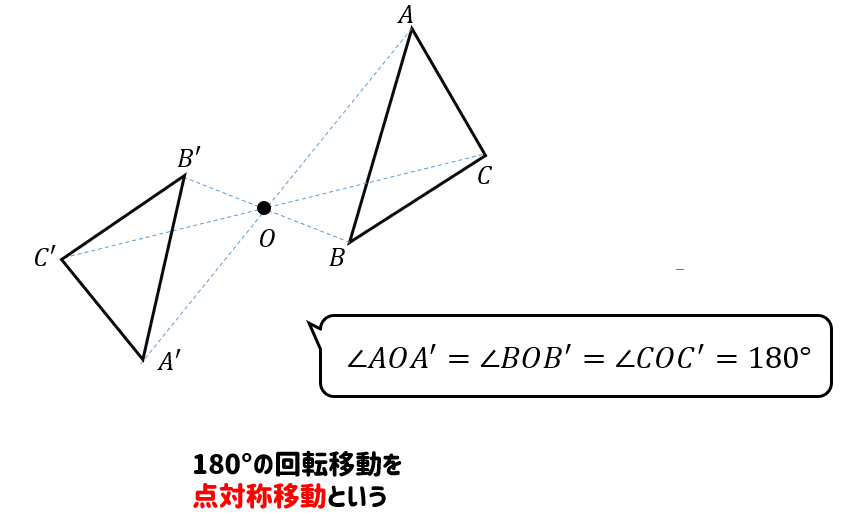
点対称移動した図形を作図せよ。
と言われたら、180°に回転移動させた図形を作図せよってことですね!
回転移動の作図
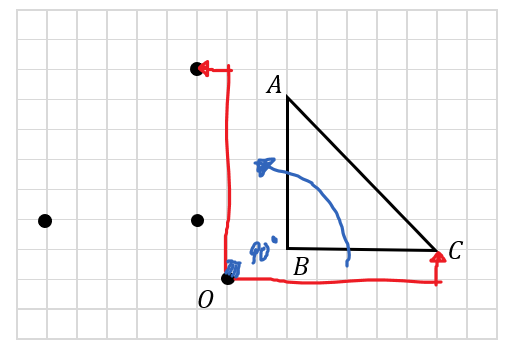
次の図の△ABCを、点をOを中心として反時計回りに90°回転移動した三角形を作図しなさい。
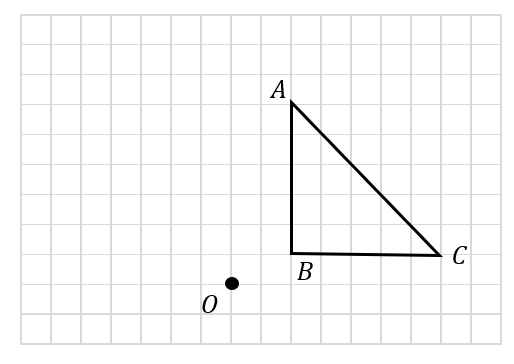
90°の回転移動では
中心から頂点までの矢印を作って考える
というのがポイントです。
どういうことなのか図を見ながら確認してみましょう。
まずは頂点Aを移動させてみます。
点Oから頂点Aまでの矢印を作ってみます。
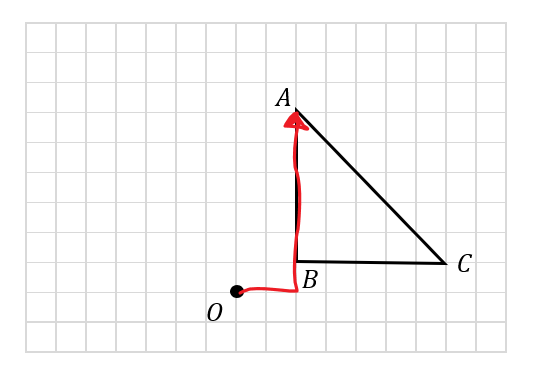
すると、こんな感じで矢印が作れます。
そして、この矢印をパタンと90°倒す感じで点を移動させます。
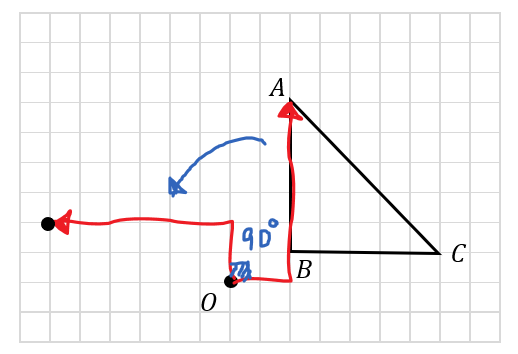
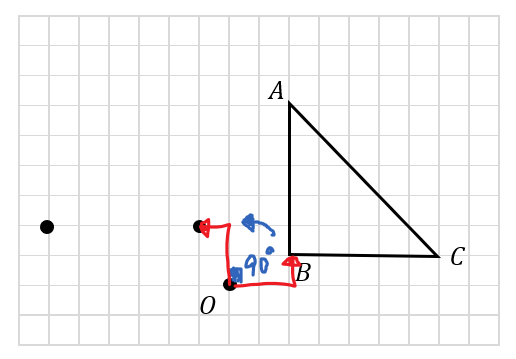
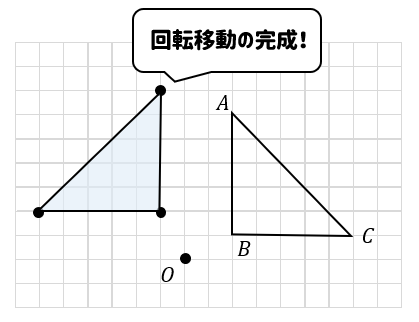
あとは、点Bと点Cも同じように移動させていけば90°の回転移動が完成します。
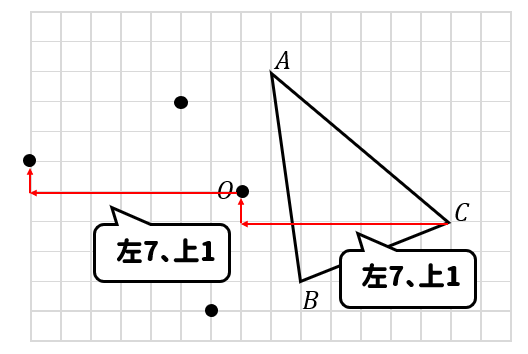
次の図の△ABCを、点をOを中心として点対称移動した三角形を作図しなさい。
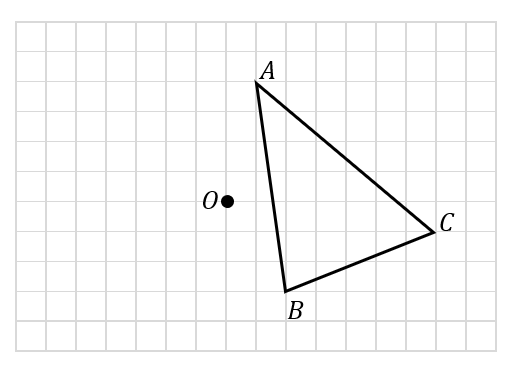
点対称移動は簡単!
各頂点から中心までの移動を調べ、中心から同じだけ移動したところに点を取ります。
まずは頂点Aの移動を考えてみましょう。
点Aから点Oまでは、左1と下4だけ移動すればいいですね。
今度は点Oから反対側に、これと同じだけ移動したところに点を取ります。
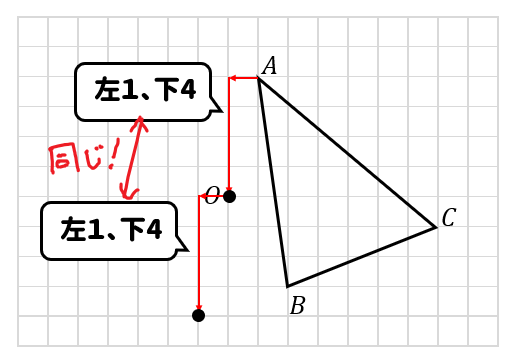
これを点B、点Cでも同じように移動させながら点を取っていきましょう。
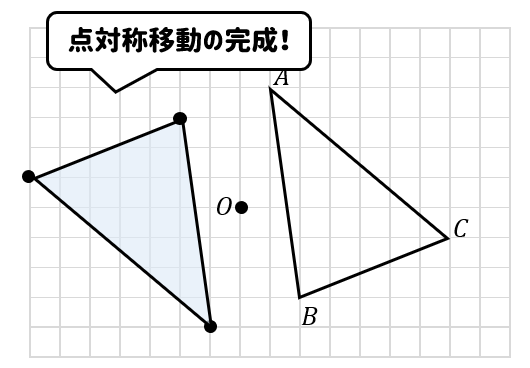
最後に点を結ぶと、点対称移動の完成です!
また、回転移動した図形ではなく
回転の中心を作図せよという問題もあります。
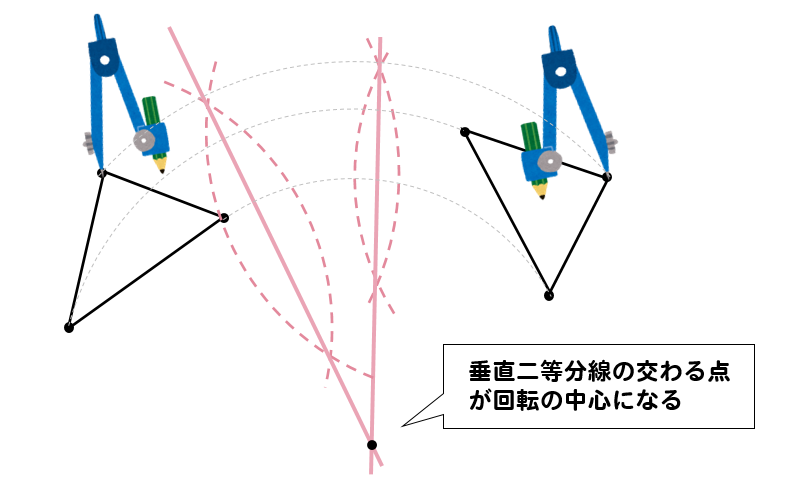
回転の中心は、対応する点の垂直二等分線が交わる点
となります。覚えておきましょう!
中心の作図はこちらの記事でも詳しく解説してるので参考にしてみてください(/・ω・)/
⇒ 【作図】回転移動の中心を求める方法とは?作図の方法を解説!

回転移動して重ねられる図形はどれ?
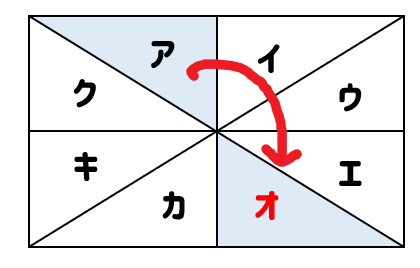
次の図において、アの図形を点Oを中心とする回転移動をして重ねることができる図形を答えなさい。
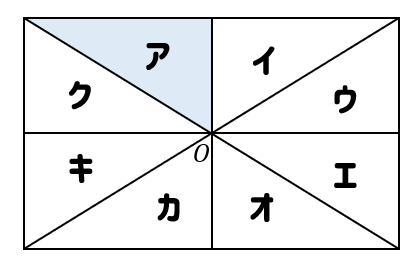
回転移動とは、その名の通り回転させる移動のことでしたね。
なので、図形アを回転させたときに重なる図形を見つければOKです。
すると、次のように図形オと重なることが分かります。
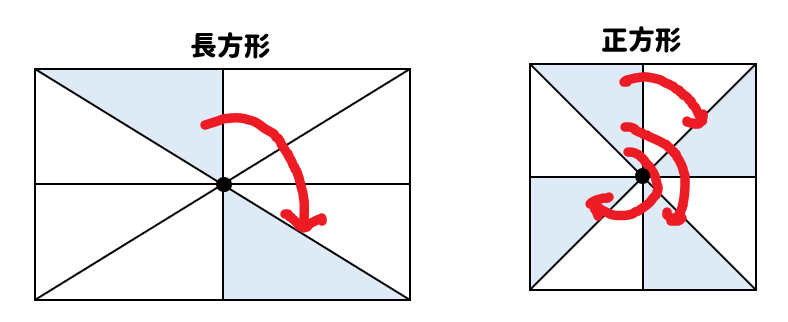
もしも、図形が正方形のときには次のように重なる図形が多くなりますね。
まとめ!
最後にもう1度、回転移動の特徴を確認しておきましょう!

回転移動とは、ある点を中心として図形をある角度だけ回転させる移動のこと。
このとき、中心とした点のことを回転の中心といいます。
また、180°の回転移動を点対称移動というので覚えておきましょう!
回転移動の作図はちょっと難しい…
特に90°の回転は慣れが必要です。

このように中心から頂点までの矢印を作って
その矢印を90°だけパタンと倒すイメージで点をとりましょう。
点対称移動の作図は、各頂点から中心までの移動を考え
点をとるようにしましょう。

















えぇぇええぇええええぇえ回転移動で困ってた自分がバカに思えるくらいわかりやすいですすすすす
回転移動って難しいですよね…(^^;)
でも、上手く理解してもらえたみたいで嬉しい^^
回転移動難しいですね
たしかにね…
回転移動は難しいけれどもこれを見て教科書に書いてある意味が分かりました!!
これを見て教科書に書いてある意味が分かりました!!
50分間授業受けてわかんなかった事がこのサイトですぐに理解できた。ありがとうございました( * . .)”
お役に立てて嬉しいです^^
定期テスト勉強で回転移動が分からず困っていましたが、これを見て理解出来ました!
分かりやすかったです
ありがとうございます♀️
お役に立てて嬉しいです^^
テスト応援してます!
予習をしていて、教科書にも回転移動の作図の仕方が載っていなくて、困っていました!
ありがとうございますとても分かりやすかったです!
ありがとうございます^^
回転移動むずい
すごくわかりやすいですありがとうございます
すごくわかりやすいですAR