今回は中学1年生で学習する空間図形の単元から
「ねじれの位置」
というものについて解説していきます。
ねじれって何だよ…
って思っちゃいますが、ちゃんと意味を理解すれば簡単な話だよ(^^)
この記事を通して、ねじれの位置をマスターしちゃいましょう!
ねじれの位置の意味
空間内にある直線は次の3つに分類することができます。
2つの直線が交わる、平行である場合
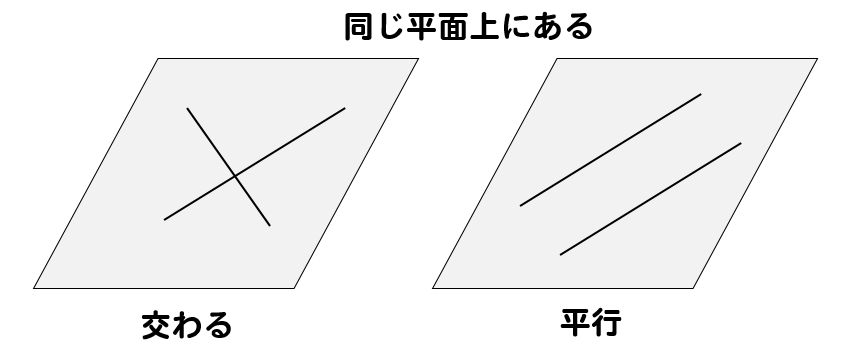
このように2直線は同じ平面上にあるということが言えます。
2直線が同じ平面上にあるというのは、その2直線の上に平らな板を置くことができるという意味ですね。
そして、もう1つが2直線が交わらず、平行でもない場合です。
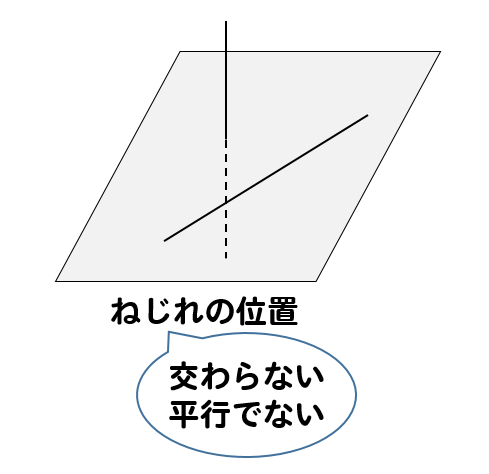
このような位置関係にある2直線をねじれの位置と言います。
つまり、ねじれの位置とは
交わらない
平行でもない
という2直線のことを言います。
ちょっと難しい言い方をすると
同じ平面上にない
と言うこともできます。
ねじれの位置の見つけ方
それでは問題を使って、ねじれの位置を見つける練習をしていましょう。
次の直方体において、辺AEとねじれの位置にある辺を見つけましょう。
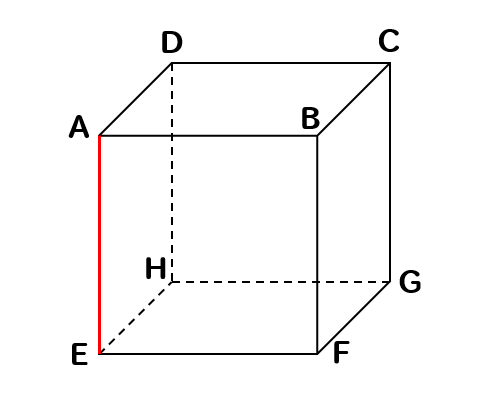
ねじれの位置とは
交わらないし、平行でもない辺のことでしたね。
つまり
辺AEと交わる辺、平行な辺を見つける。
それ以外の辺がねじれの位置!
というように考えていくと見つけやすいです。
まずは辺AEと交わる辺を見つけて除外していきましょう。
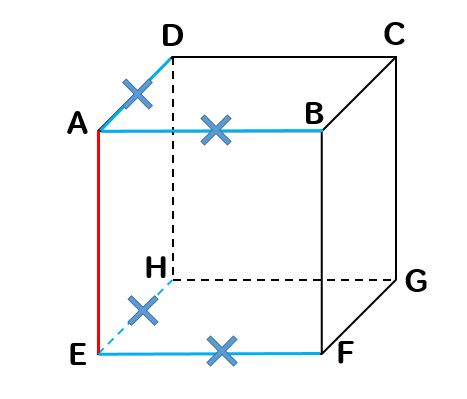
すると、このように4つの辺が除外されます。
次に、辺AEと平行な辺を見つけて除外しましょう。
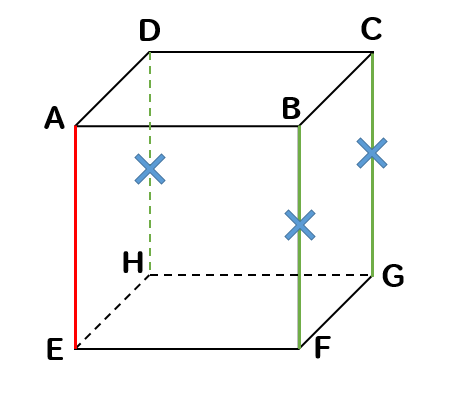
すると、このように3つの辺が除外されます。
以上より
辺AEと交わる辺、平行な辺を取り除くと
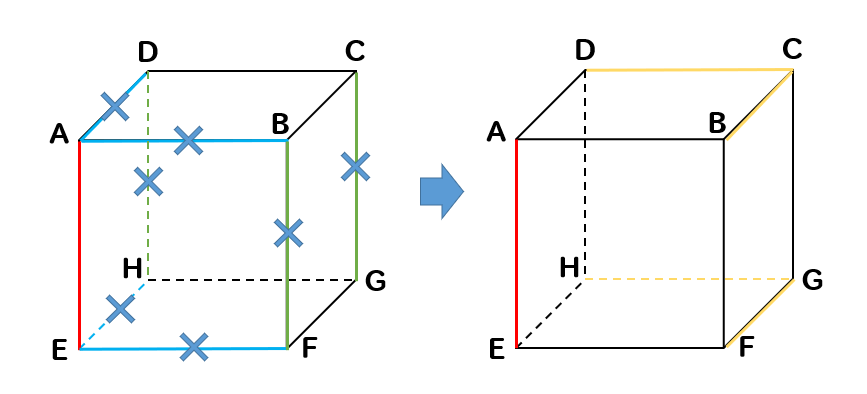
辺BC、辺DC、辺HG、辺FGが残りました。
これがねじれの位置ということになります。
ねじれの位置を見つけたいとき
交わる辺、平行な辺を取り除いて残ったものを見つける!
これで簡単に見つけることができますね(^^)

ねじれの位置(三角柱)
次は三角柱について、ねじれの位置を見つけてみましょう。
辺ABとねじれの位置にある辺を見つけましょう。
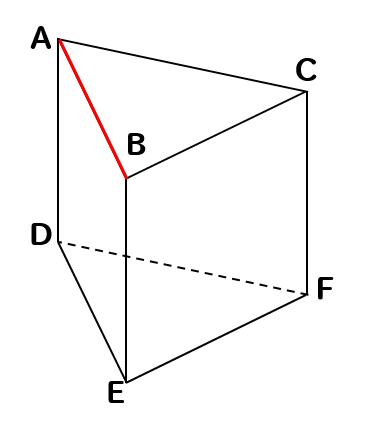
まずは、辺ABと交わる辺を除外します。
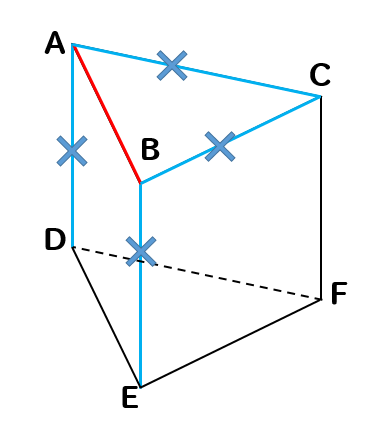
すると、このように4つの辺が取り除かれます。
次に辺ABと平行な辺を除外します。
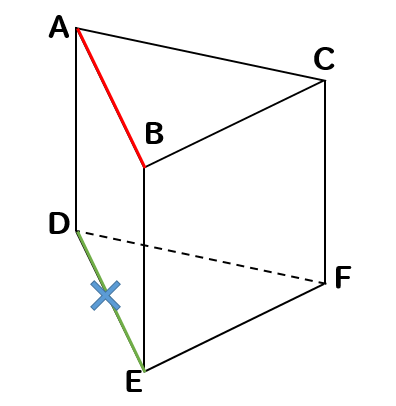
すると、このように1つの辺が取り除かれます。
以上より、残った辺がねじれの位置となります。
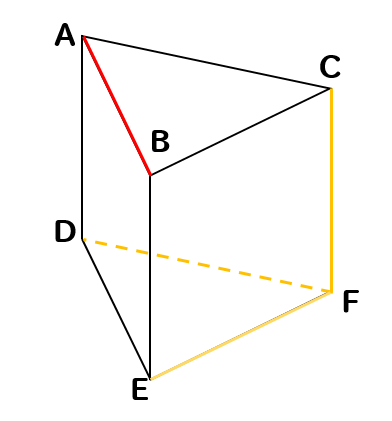
よって、辺DF、辺EF、辺CFがねじれの位置になります。
ねじれの位置(三角錐)
次は三角錐です!
次の三角錐において辺ABとねじれの位置にある辺を見つけましょう。
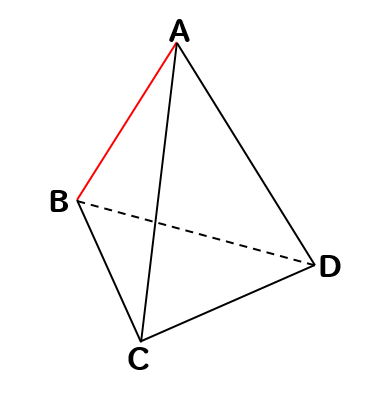
辺ABと交わる辺を除外しましょう。
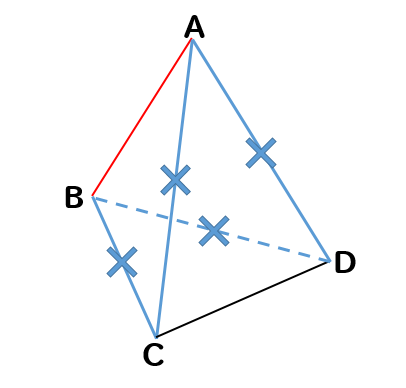
すると、このように4つの辺が取り除かれます。
辺ABと平行な辺はないので、残った辺は…
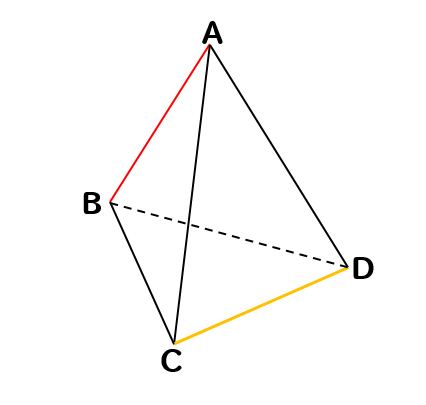
辺CDがねじれの位置となります。
ねじれの位置(五角柱)
次は五角柱だ!
次の五角柱において、辺ABとねじれの位置にある辺を見つけましょう。
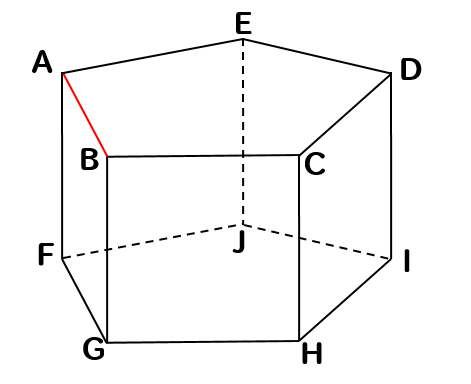
まずは、辺ABと交わる辺を除外します。
ここで注意しておきたいのは、ぱっと見て交わっているように見えなくても
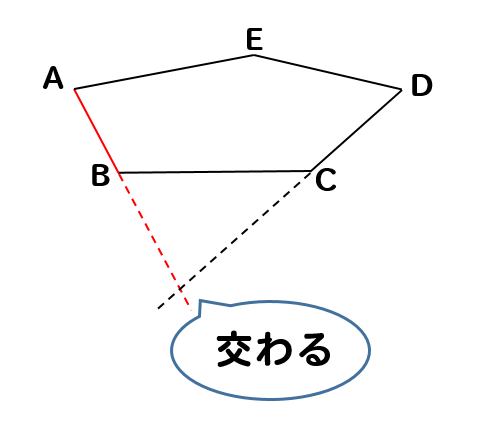
このように辺を伸ばしたときに交わってしまうものは除外してやりましょう。
すると、辺ABと交わる辺は
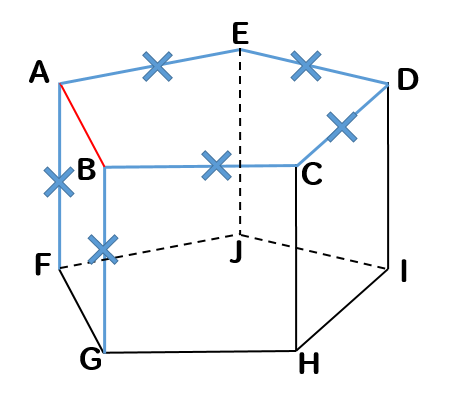
このようになりますね。
次に辺ABと平行な辺を除外しましょう。
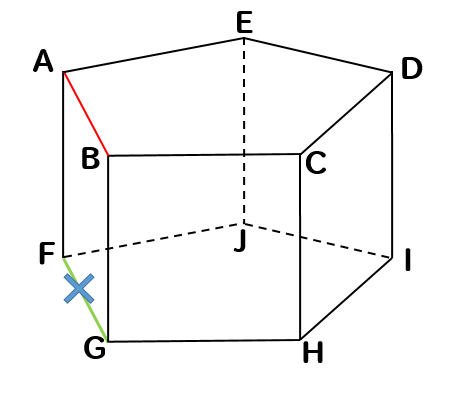
すると、このように1つ取り除かれます。
以上より、残った辺は
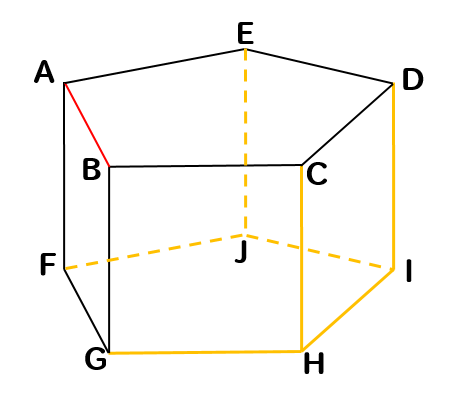
辺EJ、辺DI、辺CH、辺FJ、辺JI、辺GH、辺HIの7つの辺がねじれの位置となります。
台形を底面に持つ四角柱
次はちょっと応用な立体です。
次の立体において、辺ABとねじれの位置にある辺を見つけていきましょう。
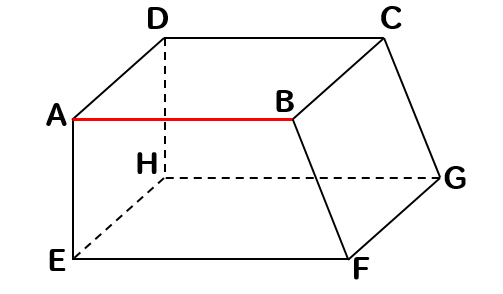
まずは、辺ABと交わっている辺を除外します。
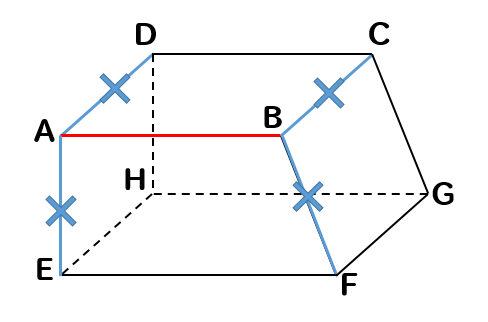
すると、このように4つの辺が取り除かれます。
次に辺ABと平行である辺を除外しましょう。
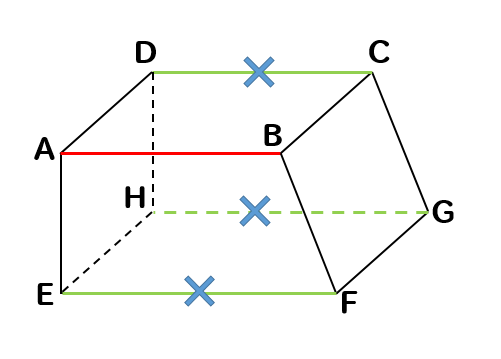
すると、このように3つの辺が取り除かれます。
以上より、残った辺は…
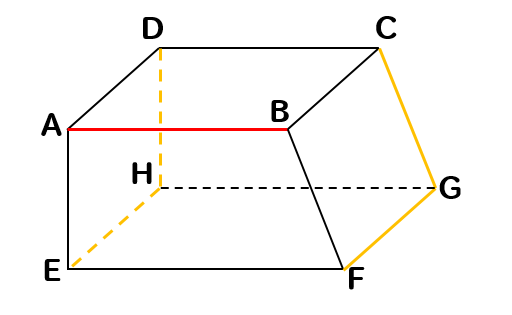
辺DH、辺CG、辺FG、辺EHがねじれの位置となります。
立方体から三角錐を切り取った立体
次の立体において、辺ABとねじれの位置にある辺を見つけましょう。
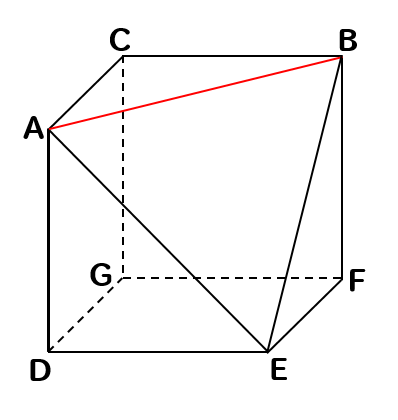
まずは、辺ABと交わるところを除外します。
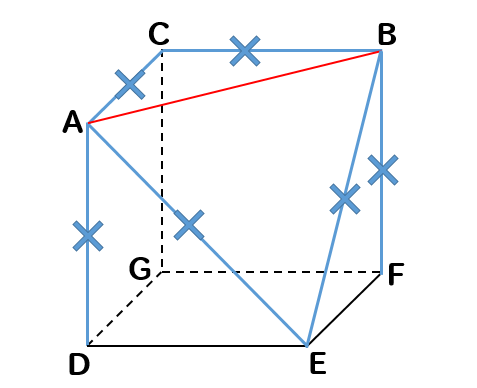
そして、辺ABと平行な辺はないので
残った辺は…
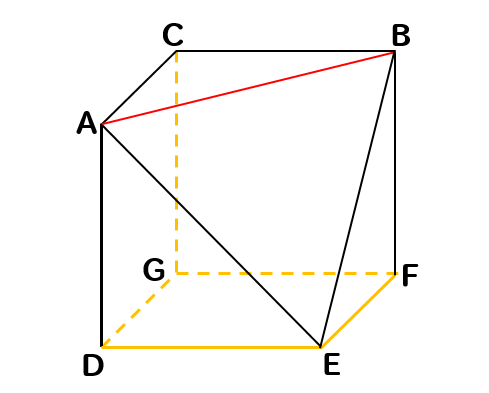
辺CG、辺DG、辺DE、辺EF、辺FGがねじれの位置となります。
まとめ
お疲れ様でした!
いろいろな立体において、ねじれの位置を見つける練習をしてみましたが理解は深まりましたか?
見つけ方の手順はシンプルでしたね。
- 交わる辺を除外
- 平行な辺を除外
- 残った辺がねじれの位置だ!
この3つの手順を踏めば、どんな立体であろうが大丈夫!
すぐにねじれの位置を見つけることができます(^^)

















マジでわかりやすかったですわかりやすかったです
ありがとうございます!!
教科書では意味が分からなかったのですが、このサイトのおかげで理解できました!本当にありがとうございます!!