おうぎ形の周りの長さを求めなさい。
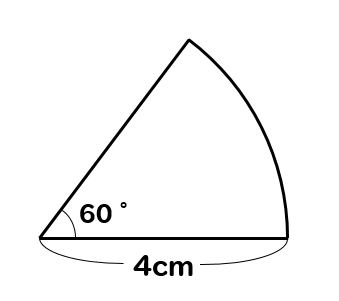
そんなの楽勝じゃーん！
ちょっと待って！！
周りの長さって、どこの部分かわかる？
えっ？
今回の記事は、こちらの動画でも解説しています(/・ω・)/
おうぎ形の周りの長さって？
勘違いしている人が多いので、ちょっと確認しておこう。
おうぎ形の周りの長さというのは
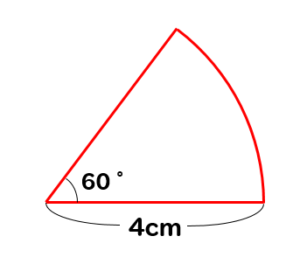
この赤線部分ですね。
つまり
弧の長さと半径2個分を合わせた長さのことです。
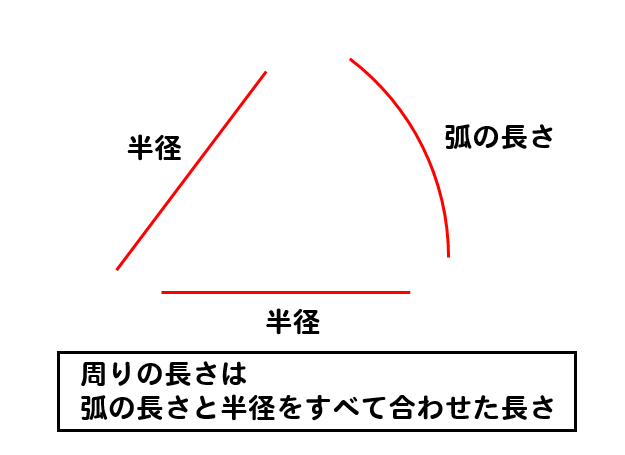
周りの長さと弧の長さを混同している人がいるので気を付けてくださいね。
それでは、おうぎ形の公式をまとめておくので
これを参考に問題に挑戦してみよう！
r：半径 a：中心角
おうぎ形の弧の長さ
$$2\pi r\times\frac{a}{360}$$
おうぎ形の面積
$$\pi r^2\times\frac{a}{360}$$
おうぎ形の周りの長さ
$$2\pi r\times\frac{a}{360}+2r$$
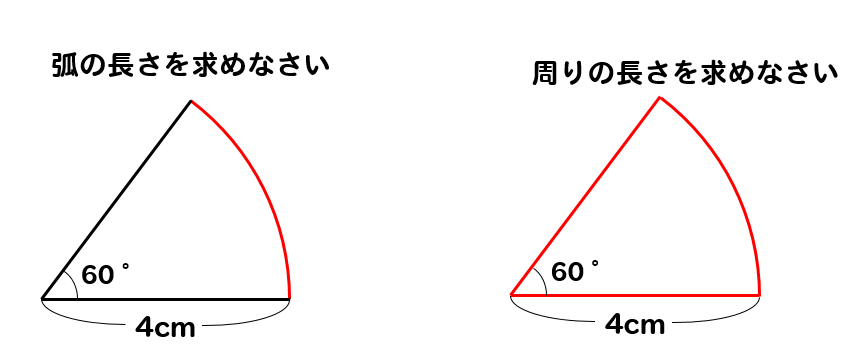
問題に挑戦してみよう！
問題
次のおうぎ形の周りの長さを求めなさい。
周りの長さとは、弧の長さと半径を2個分合わせた長さのことでしたね。
まずは弧の長さを求めてみましょう。
弧の長さの公式に当てはめてみると
$$2\pi\times4\times\frac{60}{360}$$
$$=8\pi\times\frac{1}{6}$$
$$=\frac{4}{3}\pi$$
弧の長さは\(\frac{4}{3}\pi\)とわかります。
ここに半径2個分を加えてやれば
周りの長さになります。
よって
$$\frac{4}{3}\pi+4\times2$$
$$=\frac{4}{3}\pi+8$$
よって、答えは\(\frac{4}{3}\pi+8\)(cm)となります。
見た目が変な感じですが、これでOKです！
πがついている文字と＋8はこれ以上計算できないですからね(^^)
まとめ
おうぎ形の周りの長さを求めるときには
弧の長さを求めるだけでなく
半径を2個分加えてやることを忘れないようにしてくださいね。
出てくる答えも
文字と数の足し算という
見た目が変な感じになりますが
それで合っているので大丈夫！
間違っても
こんな計算をしないように気を付けてくださいね。
おうぎ形の周りの長さを求める方法とは？ ←今回の記事
効率よく学習を進めていきたい方は必見！
この記事を通して、学習していただいた方の中にはもっといろんな単元の学習を進めていきたい！
という素晴らしい学習意欲を持っておられる方もいる事でしょう。
だけど
どこの単元を学習すればよいのだろうか。
何を使って学習すればよいのだろうか。
勉強を頑張りたいけど 何をしたらよいか悩んでしまって
手が止まってしまう…
そんなお悩みをお持ちの方もおられるのではないでしょうか。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで
どの単元を学習すればよいのか 何を解けばよいのか
そういった悩みを全て解決することができます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
- 費用が安い！月額980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
今までの悩みを解決し、効率よく学習を進めていきましょう。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
数スタの公式LINEを開設しました！
数スタのオンラインショップ開設！
⇒ 数スタ STORE
中3受験生向けの演習課題を無料配布中！