今回は中2で学習する
『平面図形』の単元から
おうぎ形を取り上げていきます。
おうぎ形といえば
この公式ですね。
もう覚えてくれたことと思いますが。
覚えていないと、学校の先生が
こんな恐い顔になっちゃうから
しっかり覚えておこうね。笑
ところで
おうぎ形といえば
公式を覚えておけば大丈夫！
という印象が強いのですが
こういう場合、どうしますか？
おうぎ形の半径を求めなさい。
あれ…
半径の公式なんてあったっけ…？？
というわけで
今回は、おうぎ形の半径を求める問題をピックアップして解説していきます。
いくぞー！
今回の記事は、こちらの動画でも解説しています(/・ω・)/
弧の長さから半径を求める問題
問題
中心角120°で弧の長さが4π㎝であるおうぎ形の半径を求めなさい。
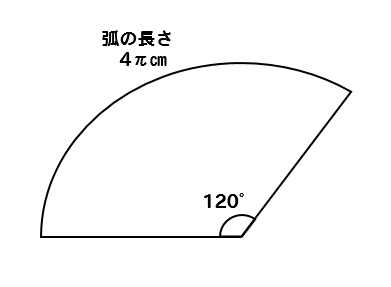
問題文に、弧の長さと中心角が与えられていて
これをヒントに半径を求めろというわけです。
この問題のポイントは
半径をxとして、方程式を作って解く！
弧の長さが与えられているので
弧の長さの公式にx、数を当てはめていきましょう。
(半径を公式通りrとして計算してもOKだからね)
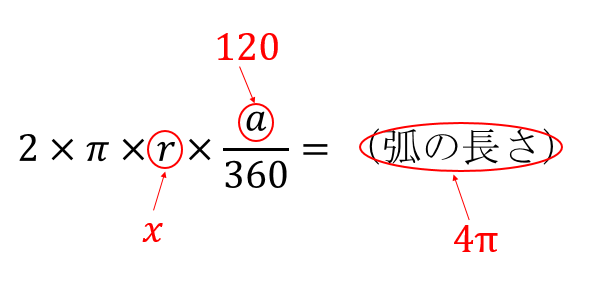
すると、このような方程式ができあがります。
$$2\pi x\times\frac{120}{360}=4\pi$$
あとは、この方程式を解いてxの値を求めれば終わりです！
$$2\pi x\times\frac{120}{360}=4\pi$$
$$2\pi x\times\frac{1}{3}=4\pi$$
両辺をπで割って、消しちゃいましょう。
$$2x\times\frac{1}{3}=4$$
両辺に3を掛けて分数を消します。
$$2x=12$$
$$x=6$$
よって、半径は6㎝と求めることができました！
半径を求める問題であっても
特に新しい公式を用いるわけではありません。
この公式を覚えておけば大丈夫です。
先生が怒るから、絶対に覚えておこう。
面積から半径を求める問題
注意！
この問題は中3で学習する『二次方程式』の知識を使います。
中1の方は、まだ解けなくても大丈夫です。
でも、まぁ、いずれはね。
問題
面積がπ㎝²、中心角が40°であるおうぎ形の半径を求めなさい。
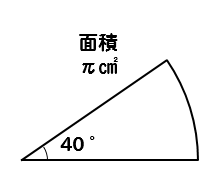
今度は面積が与えられているので
おうぎ形の面積の公式に当てはめていきましょう。
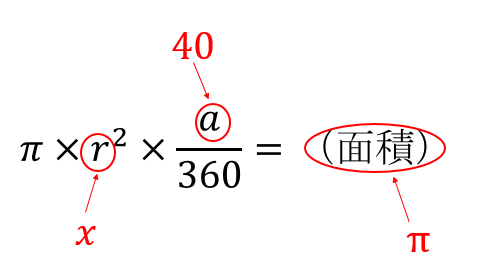
すると、このような方程式ができあがります。
$$\pi\times x^2\times \frac{40}{360}=\pi$$
これを解いていきましょう！
$$\pi x^2\times\frac{1}{9}=\pi$$
両辺をπで割って消しちゃいます。
$$\frac{1}{9}x^2=1$$
両辺に9を掛けて分数を消します。
$$x^2=9$$
$$x=\pm 3$$
ただし
半径の値は＋になるので
$$x=3$$
よって、半径は3㎝となりました。
最後に二次方程式の計算が少しだけ出てくるだけで
基本はさっきの問題と一緒でしたね(^^)
まとめ
半径を求める問題においても
大事なのは、この公式でしたね。
半径を求める問題以外でも
中心角を求める問題でも必須となるので
必ず覚えて、使えるようになっておこう！
おうぎ形の半径を求める問題を解説！←今回の記事
円周率をπとし、面積が３π、中心角が80°であるおうぎ形の半径の長さを求めなさい。
コメントありがとうございます(^^)
Twitter上に解説をアップしました。
多分、合っているとおもうのですが…ご参考くださいませ。
式の解説してくれてありがとう。
宿題に役立ちました。
お役に立てて嬉しいです！
すごい分かりやすかったので問題がスラスラ解けました。
ありがとうごさいました。
それはよかった！
嬉しいコメントありがとうございます(^^)
役に立ちましたありがとうございます
お役に立てて良かったです！！