高校数学Ⅰで学習する2次不等式の単元から
「絶対不等式の解き方」
について解説していきます。
絶対不等式とは、どのような値をとっても成り立つ不等式のことをいいます。
そして、この絶対不等式を利用した次のような問いがよく出題されます。
すべての実数\(x\)について成り立つような定数\(k\)の範囲を求めよ。
では、今回の記事では絶対不等式を利用した問題をパターン別に例題を用いて解説していきます。
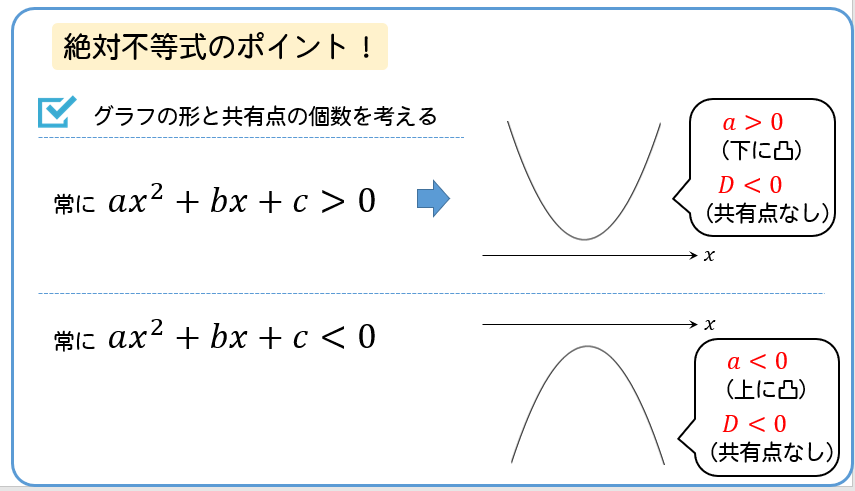
絶対不等式の問題を考える上でのポイントは以下の通りです。
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
絶対不等式の問題(グラフの形が決まっている)
【問題】
すべての実数 \(x\) について,2次不等式 \(x^2+2kx-3k+4>0\) が成り立つような定数 \(k\) の値の範囲を求めよ。
\(x^2\) の係数が正であることから、グラフの形が下凸の放物線であることは簡単に読み取れますね。
そして、このグラフが常に「\(>0\)」となるのは、
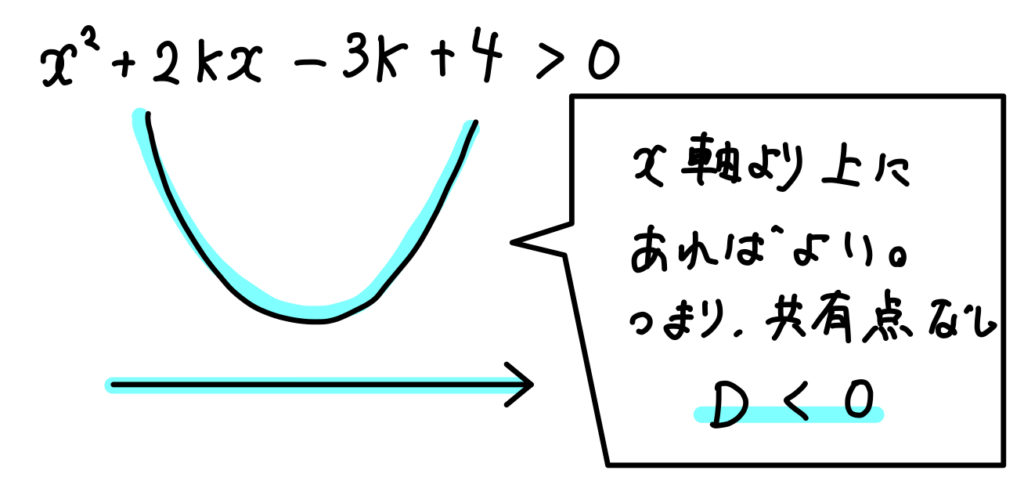
このように、\(x\)軸の上側にあればよい。
つまり、\(x\)軸との共有点を持たなければよいってことが読み取れます。
よって、判別式の値が負となる範囲を求めていきましょう。
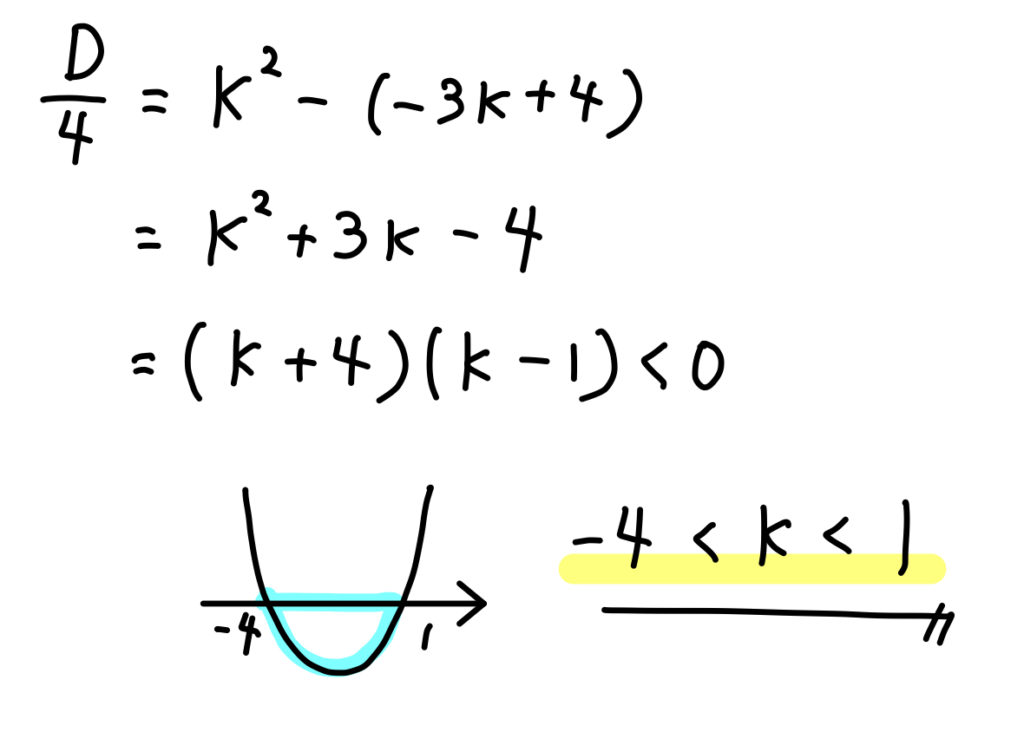
【問題】
すべての実数 \(x\) について,2次不等式 \(-x^2+mx+2m<0\) が成り立つような定数 \(m\) の値の範囲を求めよ。
今回の問題では、\(x^2\)の係数が負となるので、
常に「\(<0\)」となるためには、次のように考えていきましょう。

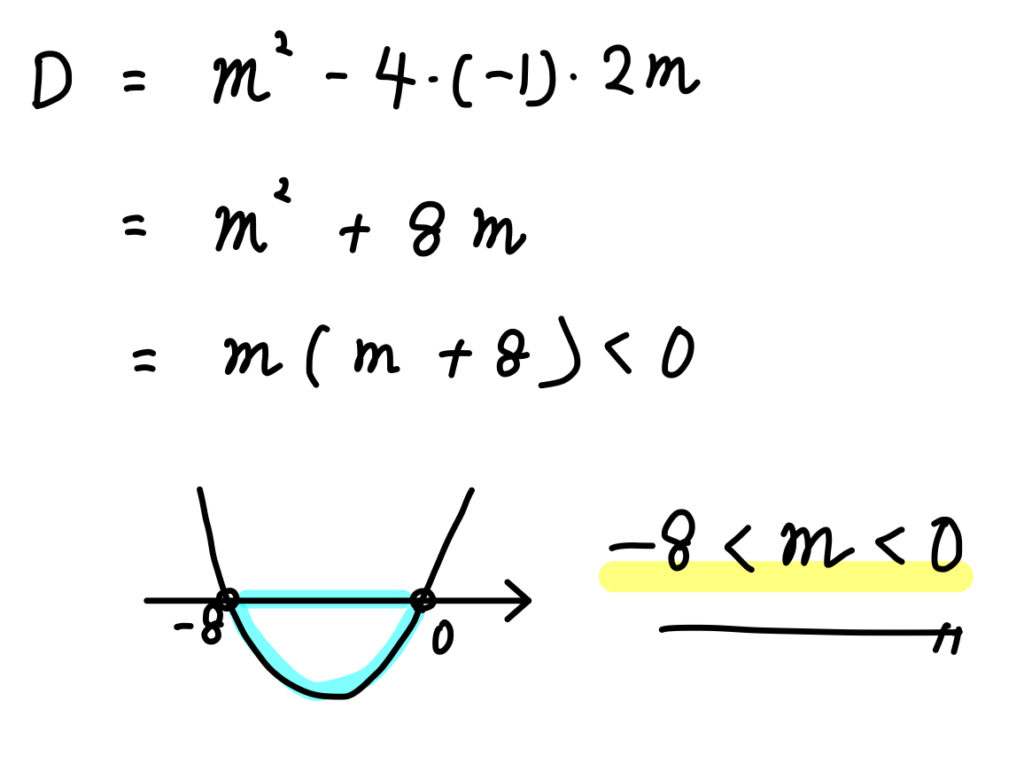
絶対不等式の不等号が「\(≧, ≦\)」のときには、次の例題のように判別式が「\(≧0、≦0\)」となることに気を付けてくださいね。
【問題】
すべての実数 \(x\) について,2次不等式 \(x^2-2x≧kx-4\) が成り立つような定数 \(k\) の値の範囲を求めよ。
まずは不等式を整理して、右辺が0になるようにしましょう。
$$\begin{eqnarray}x^2-2x&≧&kx-4\\[5pt]x^2-(2+k)x+4&≧&0 \end{eqnarray}$$
下凸のグラフで「\(≧0\)」となるには、\(x\)軸との共有点は0個または1個となればOKです。
よって、判別式は「\(D≦0\)」となればよいですね。
$$\begin{eqnarray}D&=& (2+k)^2-4\cdot4\\[5pt]&=&4+4k+k^2-16\\[5pt]&=&k^2+4k-12\\[5pt]&=&(k+6)(k-2)≦0\\[5pt]&&-6≦k≦2\cdots(解)\end{eqnarray}$$
以上のように、グラフの形が決まっているときには、\(x\)軸との共有点の個数を考えて判別式を計算していけばよいですね!
楽勝、楽勝~♪
絶対不等式の問題(グラフの形を判断する)
【問題】
すべての実数 \(x\) について,2次不等式 \(kx^2+(k+1)x+k+1>0\) が成り立つような定数 \(k\) の値の範囲を求めよ。
今回の問題では、\(x^2\)の係数が文字になっているため、不等号の向きからグラフの形を判断する必要があります。
「\(\cdots >0\)」になるためには、
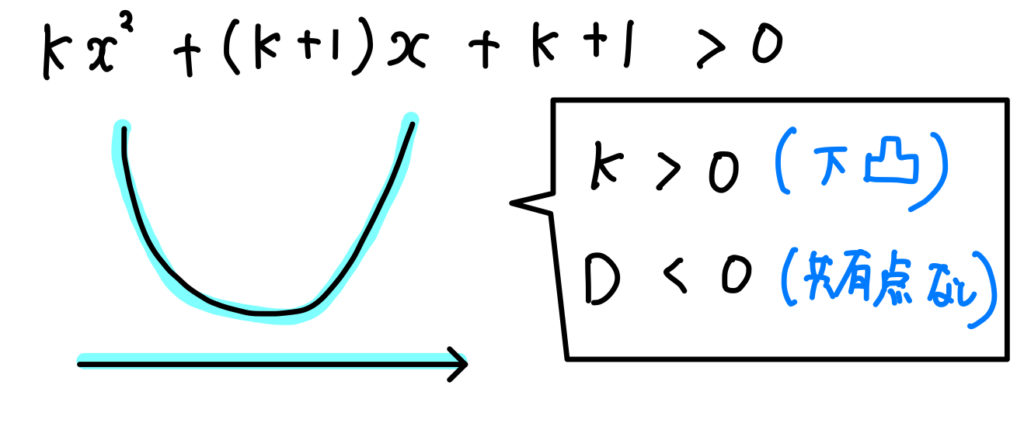
このような条件を満たす必要があります。
条件が読み取れたら、あとは判別式を使って計算していきましょう。
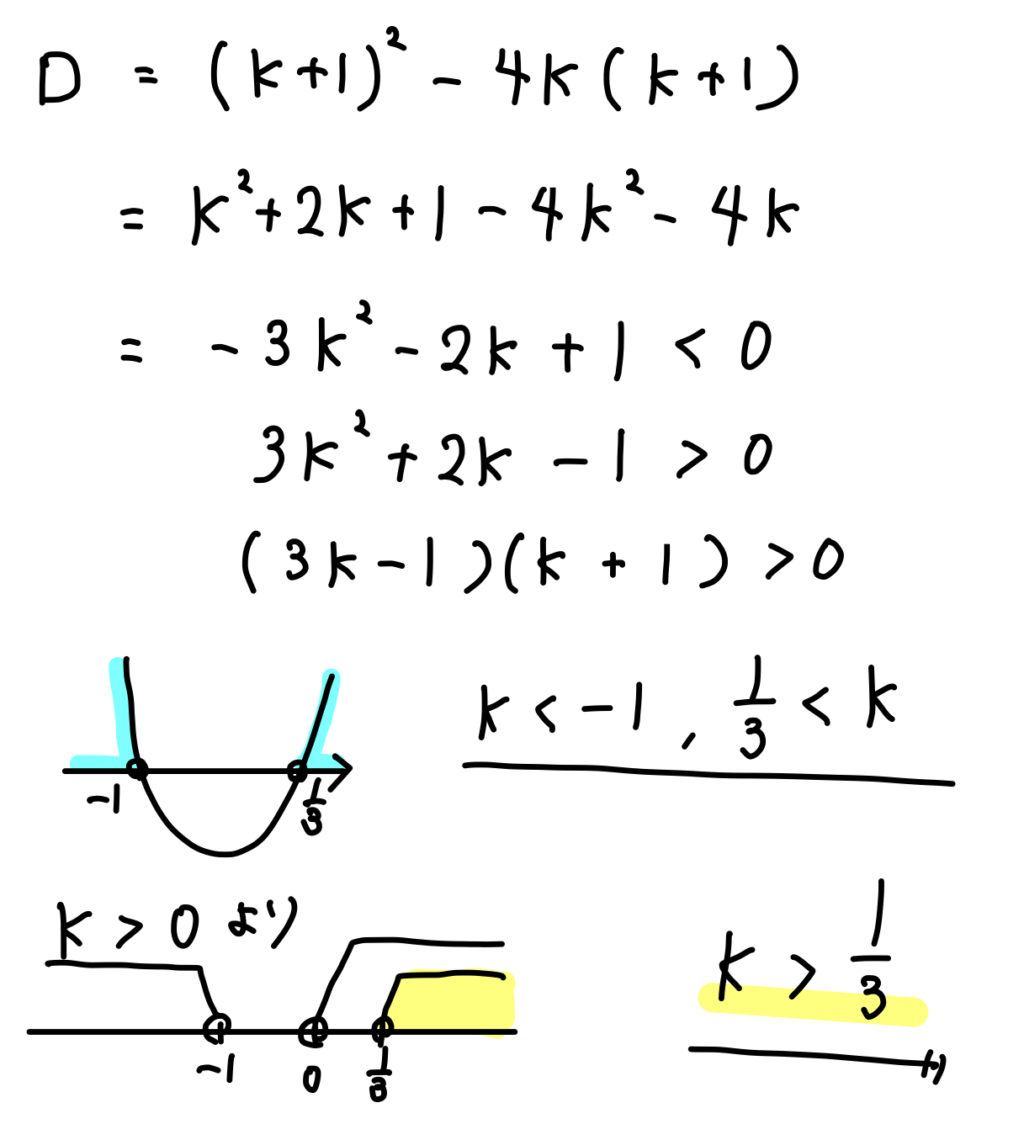
【問題】
すべての実数 \(x\) について,2次不等式 \(kx^2+(k+1)x+2k-1<0\) が成り立つような定数 \(k\) の値の範囲を求めよ。
「\(\cdots <0\)」になるためには、
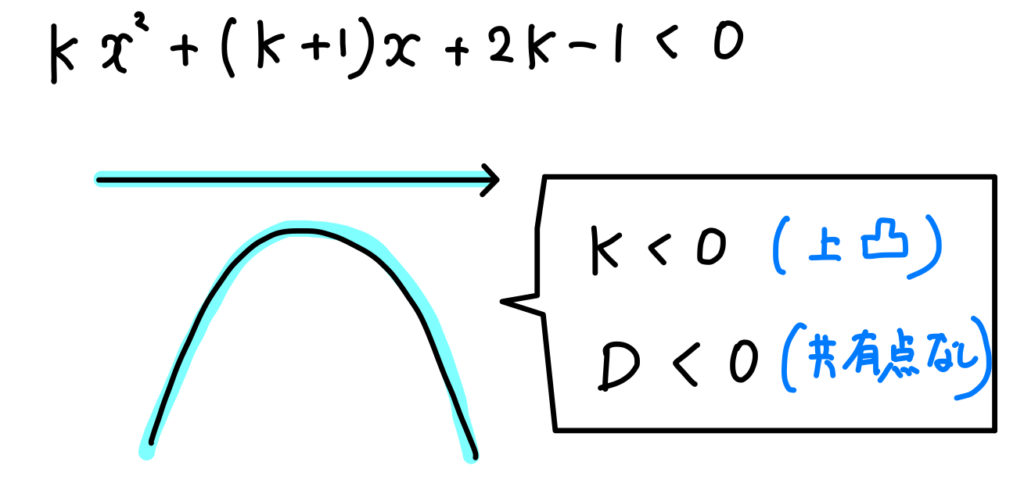
このような条件を満たす必要があります。
条件が読み取れたら、あとは判別式を使って計算していきましょう。
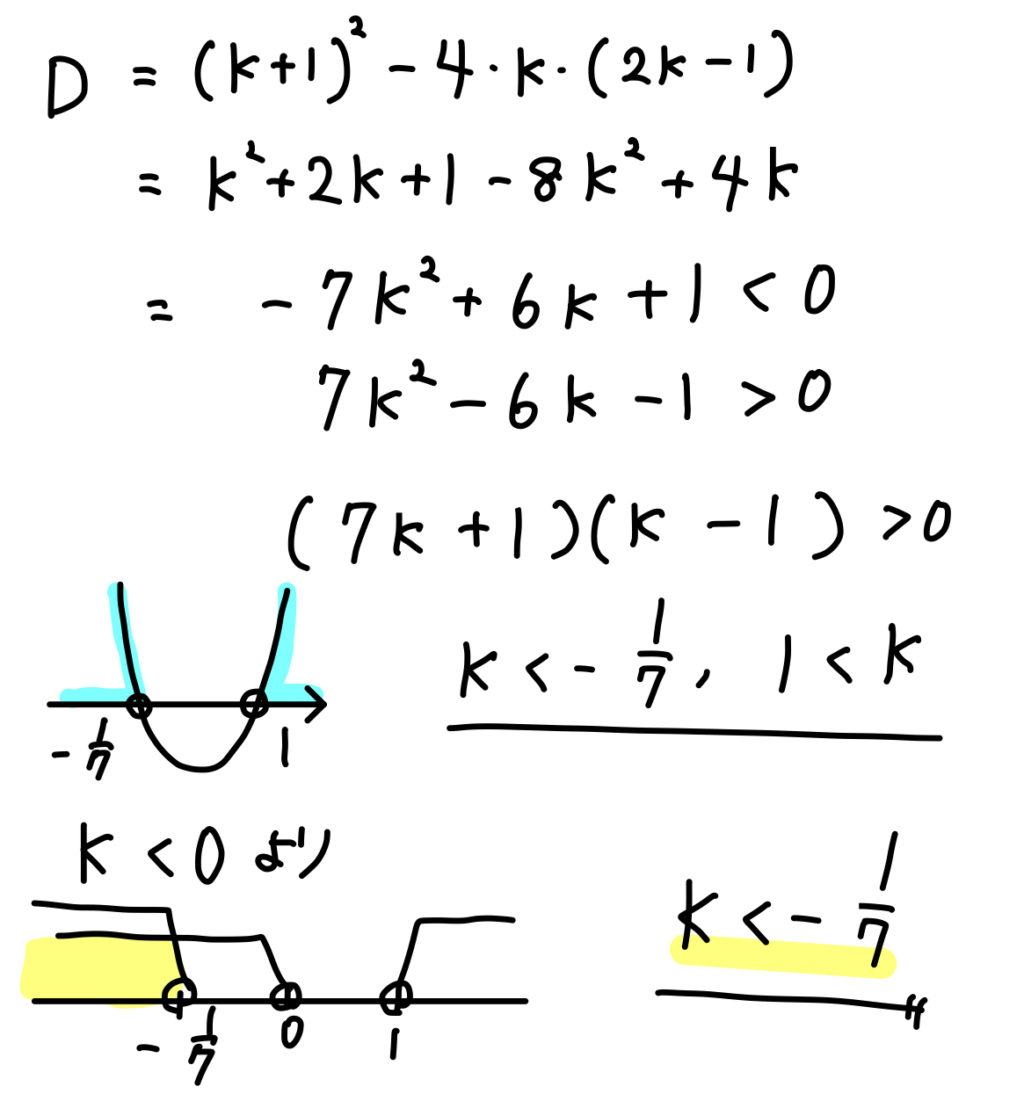
以上のように、\(x^2\)の係数が文字となっている場合には、
判別式だけでなく、グラフの形も判断し、2つの条件を組み合わせて範囲を求めていくようになります。
絶対不等式の問題(1次、2次不等式の場合分け)
【問題】
すべての実数 \(x\) について,不等式 \(ax^2-2\sqrt{3}x+a+2≦0\) が成り立つような定数 \(a\) の値の範囲を求めよ。
あれ、さっきの問題と何が違うの?
と思った方もいるかもしれませんが、問題文をよく見てみると…
「不等式 \(ax^2-2\sqrt{3}x+a+2≦0\)」
と記述されており、今までのように「2次不等式」と書かれていません。
つまり、\(ax^2-2\sqrt{3}x+a+2≦0\) は\(x^2\) の係数が0となり、1次不等式となる場合も考える必要があるということです。
というわけで、
- \(a=0\) ⇒ 1次不等式になる場合
- \(a≠0\) ⇒ 2次不等式になる場合

1次不等式になる場合、すべての実数 \(x\) について不等式を成り立たせることができないので不適。
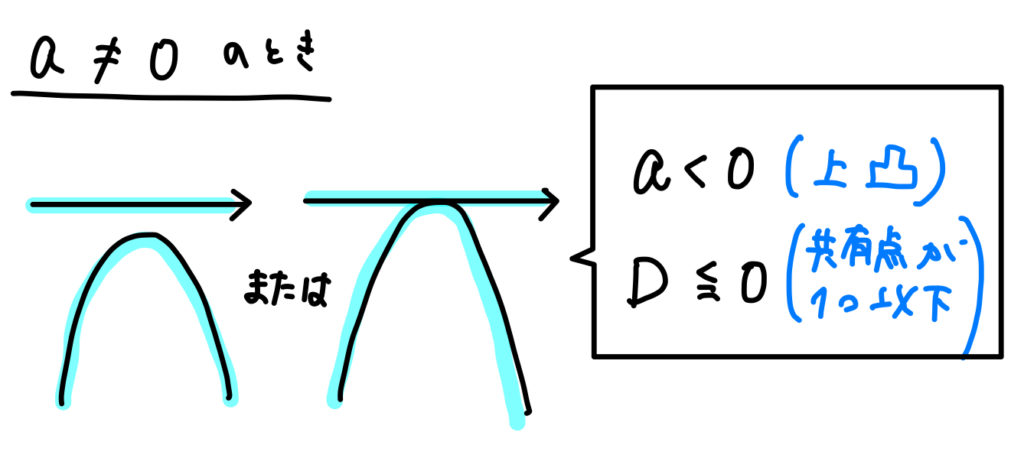
そして、2次不等式になる場合。
「\(≦0\)」を満たすためには上のような条件となります。
よって、計算を進めていくと、
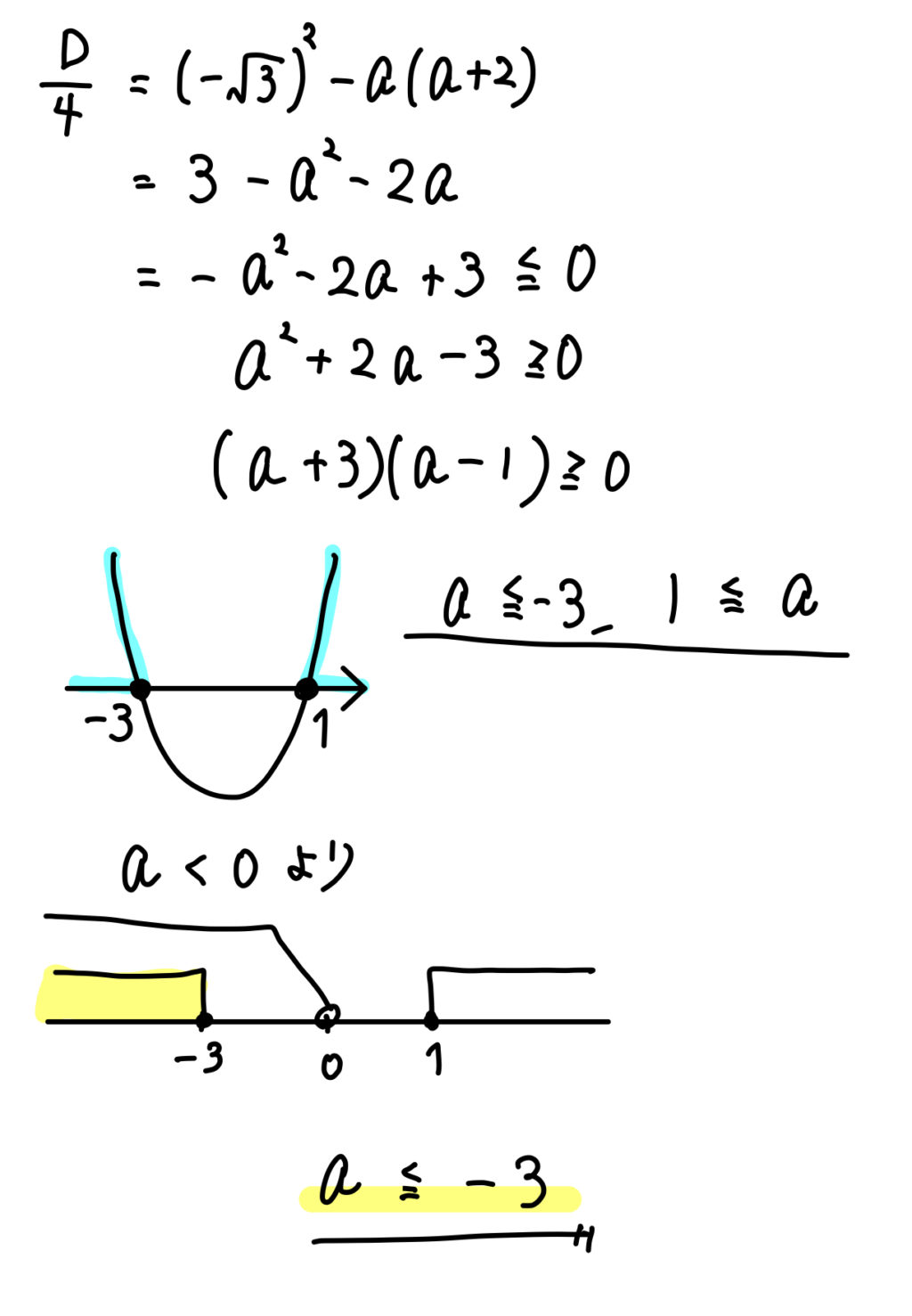
【問題】
すべての実数 \(x\) について,不等式 \((k-2)x^2+2(k-1)x+3k-5>0\) が成り立つような定数 \(k\) の値の範囲を求めよ。
\(x^2\) の係数 \((k-2)\) が0になる場合、そうでない場合で分けて考えていきましょう。

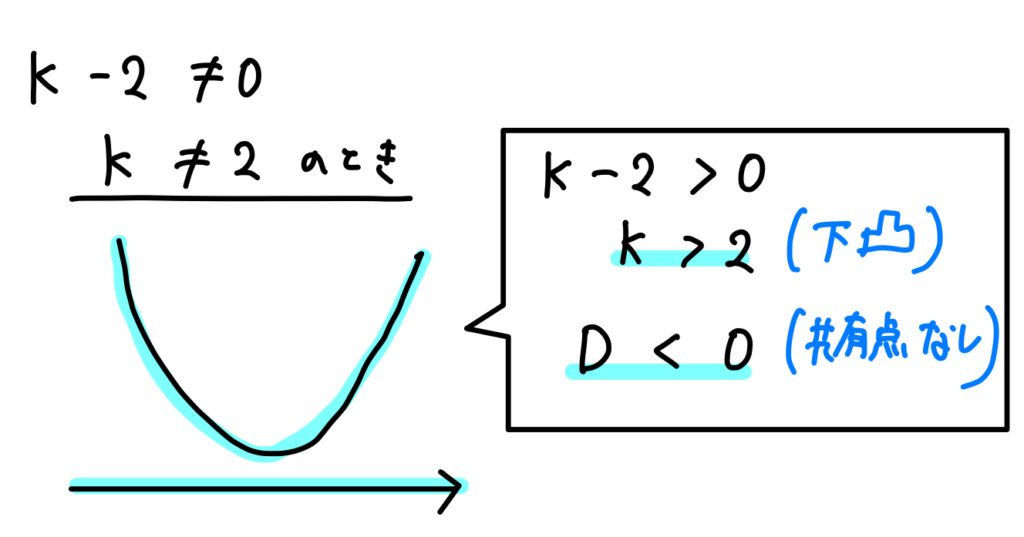
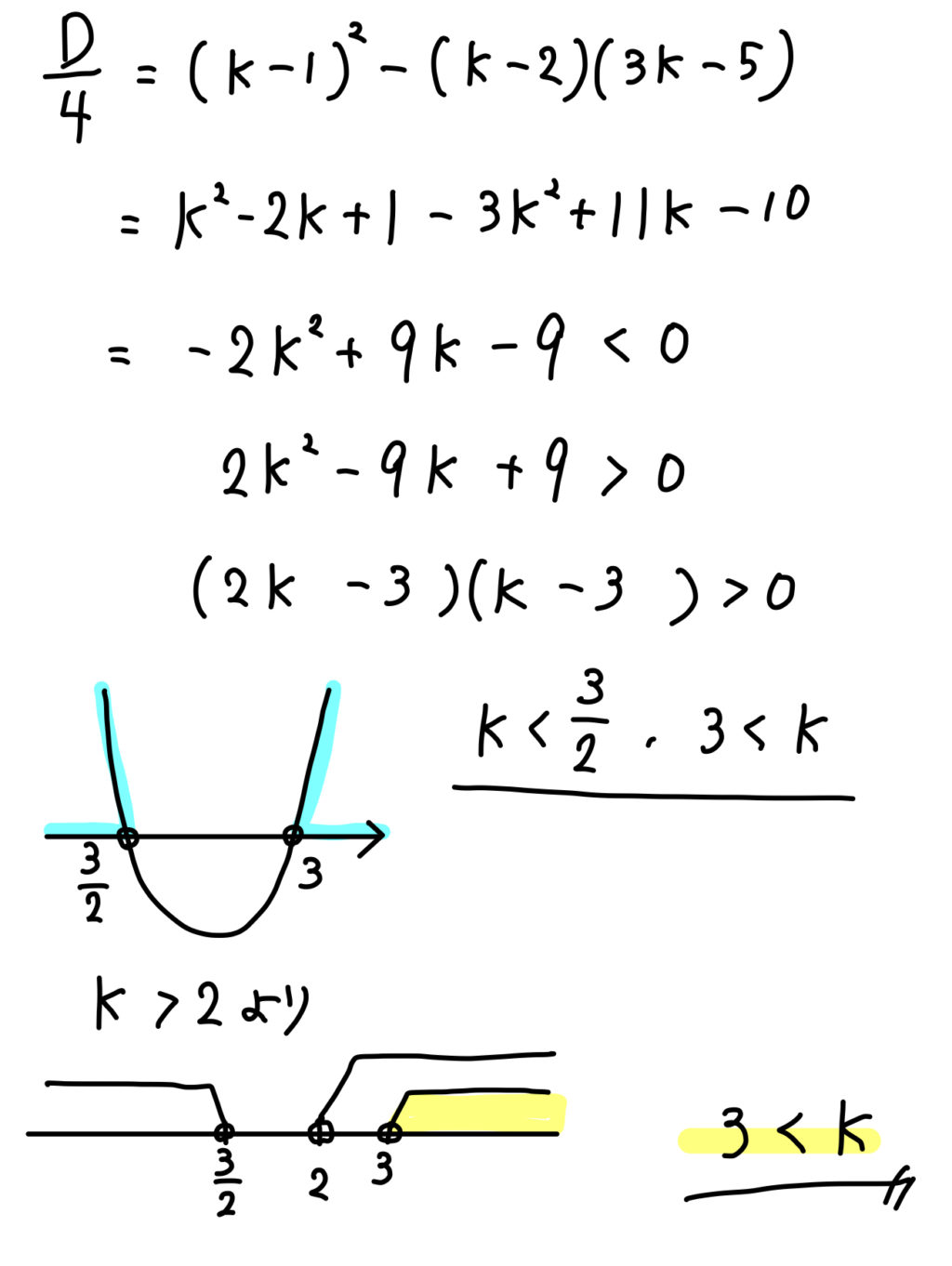
以上のように、問題文の記述をよく見て「不等式」としか書かれていない場合には、\(x^2\)の係数が0になり、1次不等式となる場合も考えていくようにしましょう。
まとめ!
お疲れ様でした!
絶対不等式を利用した問題は、グラフを使ってイメージ図を書いてみることが大事ですね。
常に「\(>0\)」ってどういうことだろう?
グラフにしてみるとどんなイメージかな?
って感じでグラフをかいてみると簡単に条件を読み取ることができますよ。
また、与えられている不等式が「2次不等式」なのか。
それとも、ただの「不等式」なのか。
ここも大きな違いとなってくるので、問題文をよく見るようにしておいてくださいね!
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説! ←今回の記事
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















x^2-2x≧kx+4の問題のDの範囲ってD≧0じゃなくてD≦0じゃないんですか?
D≧0だと共有点が1つか2つになると思うのですが…
おっしゃる通りです…
間違えていたので訂正しておきました!
ご指摘ありがとうございますm(__)m
よかったです!
いえいえ!参考になりました!