高校数学Ⅰで学習する2次不等式の単元から
「文字係数の2次不等式」
について解説していきます。
今回取り上げる問題はこちら!
【問題】
次の \(x\)についての2次不等式を解け。
(1)\(x^2-(2a+1)x+a^2+a<0\)
(2)\(x^2-(a+1)x+a≧0\)
(3)\(x^2-3ax+2a^2+a-1>0\)
(4)\(ax^2≦ax\)
【問題】
\(x^2-2x-3≦0\) , \(x^2-2(a+1)x+a^2+2a≦0\) を同時に満たす \(x\) が存在するような定数\(a\)の範囲を求めよ。
サクッと解ける基礎問題から、場合分けが必要なパターンまで。
それぞれの解き方、考え方について理解を深めておきましょう。
2次不等式の基礎についてはこちらを確認!
今回の問題はこちらの動画でも解説しています(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
問題(1)文字の大小を区別せよ!
次の \(x\)についての2次不等式を解け。
(1)\(x^2-(2a+1)x+a^2+a<0\)
解き方の流れは、これまでの2次不等式を同じです。
因数分解または解の公式を利用して、「\(=0\)」になる値を求めます。
ただし、今回の問題では次のように文字を含んだ値が出てくるので、ちょっと注意が必要です。

ポイントとしては、\(x=a,a+1\) が求まったところ。
\(a\),\(a+1\) の大小関係を理解できるかどうかですね。
\(a\)がどんな値になるかは分かりませんが、
どんな値であっても、それに1を加えた数(\(a+1\))の方が大きくなるってことは明らかですよね。
大小関係が分かれば、放物線のグラフを書くことができるようになるので、あとは今まで通り範囲を求めていけばOKってことになりますね!
問題(2)(3)文字の大小について場合分け!
【問題】
次の \(x\)についての2次不等式を解け。
(2)\(x^2-(a+1)x+a≧0\)
まずは因数分解をして、「\(=0\)」になる値を求めます。
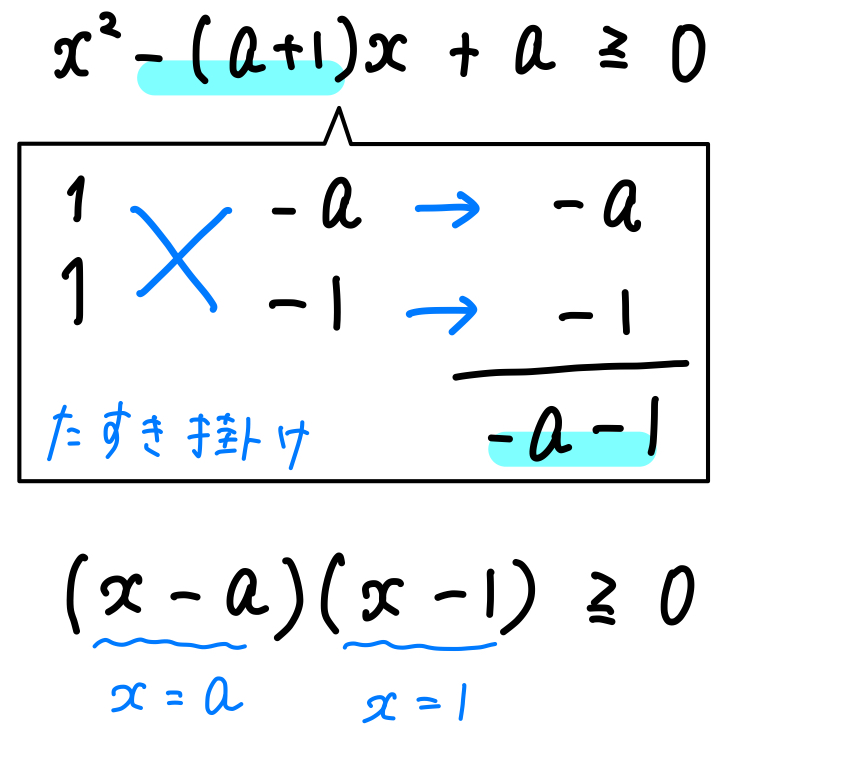
すると、\(x=a,1\) という値が求まります。
しかし、ここで困ったことが…
大小関係が分からん!
ということになります。\(a\) と \(1\) どっちが大きいか判断がつきません。
なので、仕方なく次のように場合分けをして進めていきます。
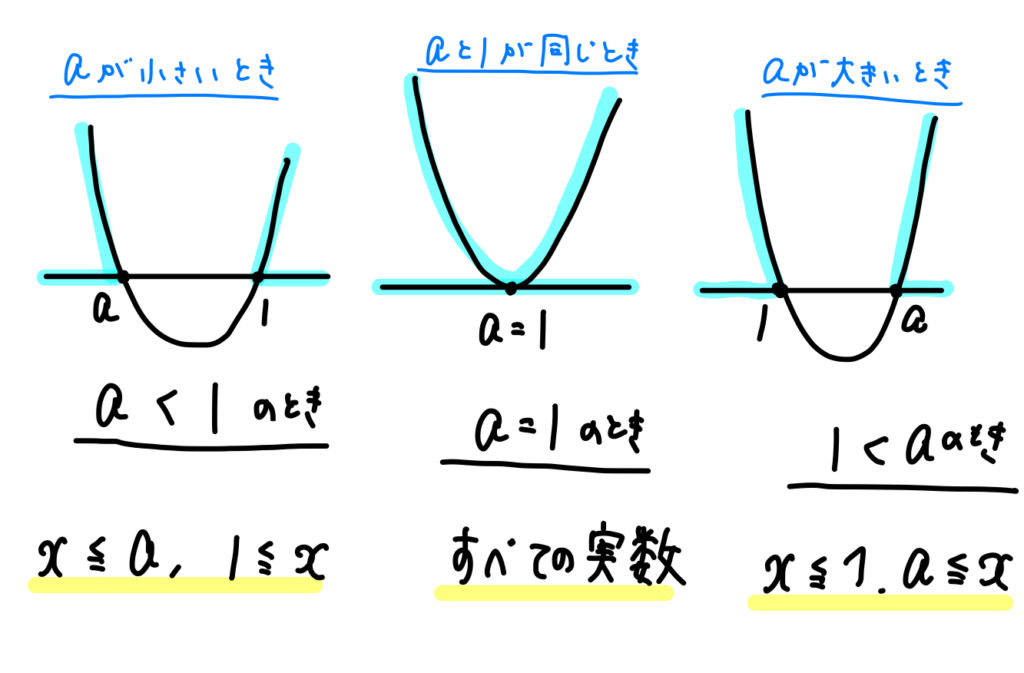
場合分けの方法としては、
- \(a\)の方が小さいパターン ⇒ \(a<1\) のとき
- \(a\)と\(1\) が同じになるパターン ⇒ \(a=1\) のとき
- \(a\)の方が大きいパターン ⇒ \(a>1\) のとき
こんな感じで考えていけばいいですね!
では、次も同じパターンになるので練習としてご活用ください。
【問題】
次の \(x\)についての2次不等式を解け。
(3)\(x^2-3ax+2a^2+a-1>0\)

問題(4)文字の正負によって場合分け!
【問題】
次の \(x\)についての2次不等式を解け。
(4)\(ax^2≦ax\)
まずは因数分解をして、「\(=0\)」になる値を求めます。

すると、\(x=0,1\) という値はすぐに求まるのですが、
\(x^2\)の係数である \(a\) に符号が分からないので範囲が求まりません。
そこで、\(a\)を場合分けして消してしまおう!という考えになります。
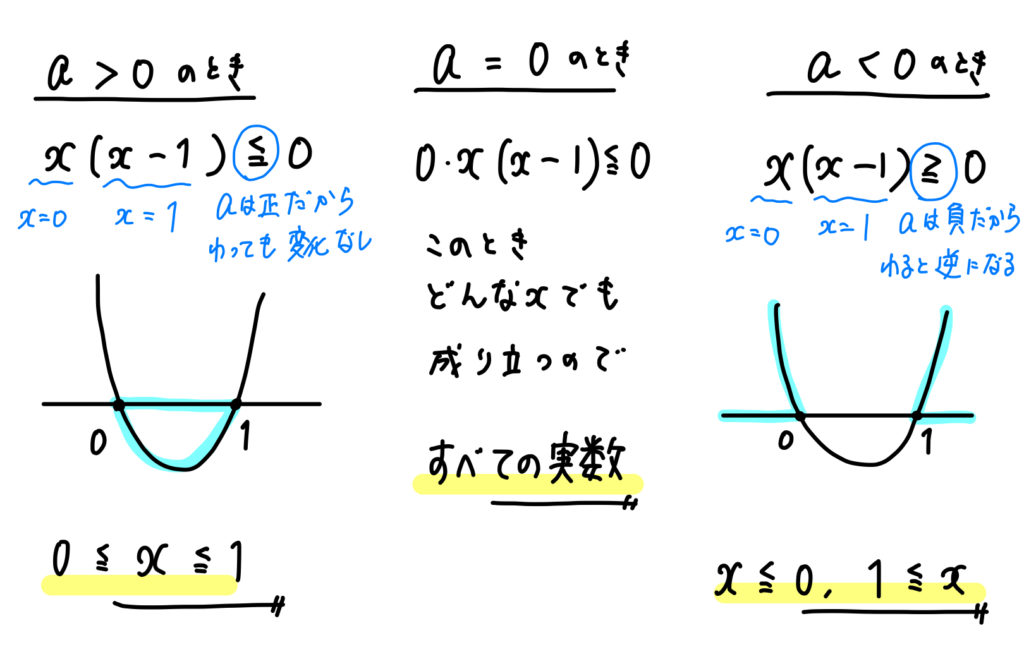
場合分けの方法としては、
- \(a\)が正 ⇒ 割っても不等号の向き変わらない
- \(a\)が0 ⇒ 割れないので、\(0\)を代入して不等式を考える
- \(a\)が負 ⇒ 割ると不等号の向きが変わる
こんな感じで考えていけばいいですね!
問題(5)数直線を使って範囲を考える!
【問題】
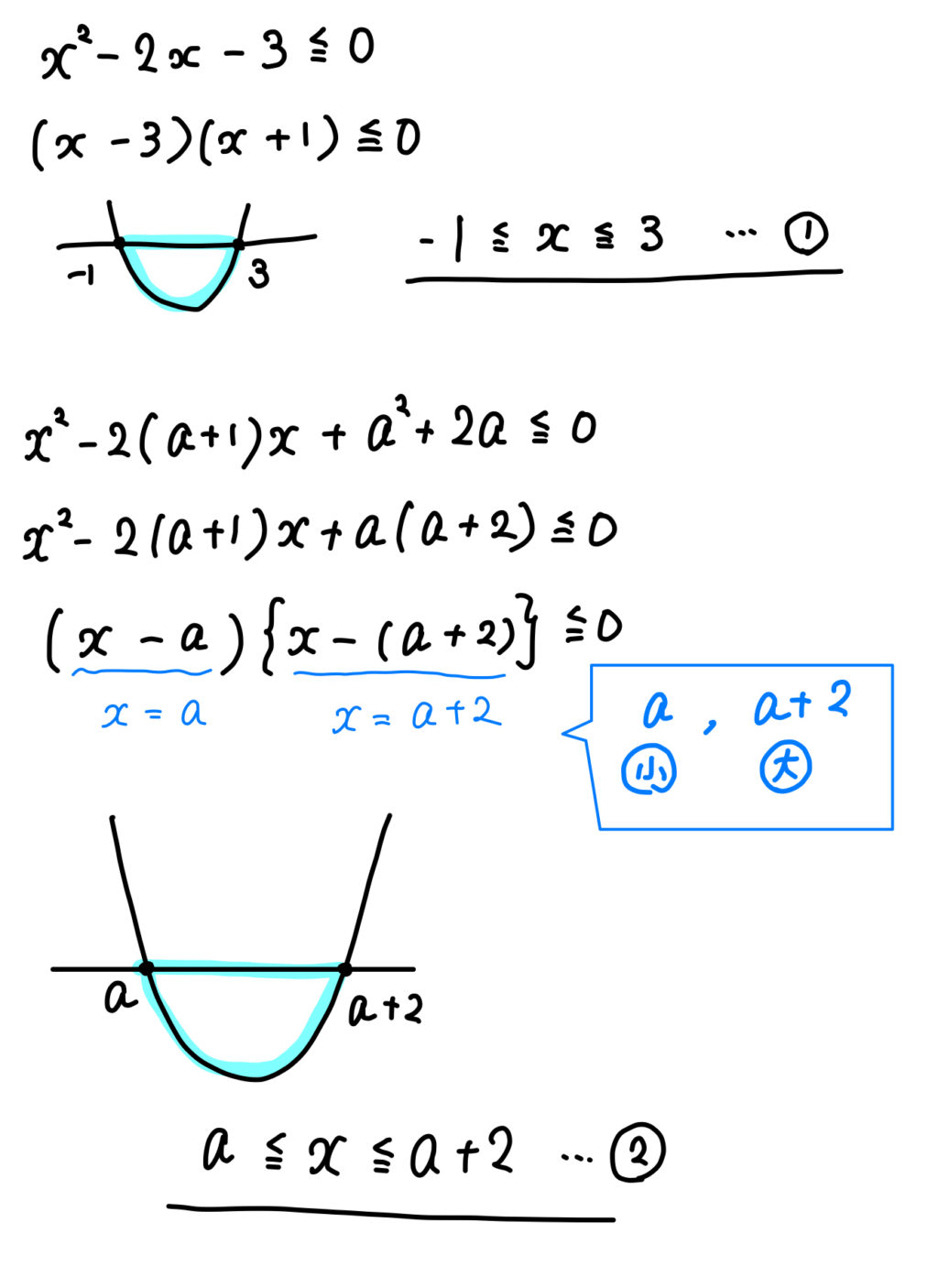
\(x^2-2x-3≦0\) , \(x^2-2(a+1)x+a^2+2a≦0\) を同時に満たす \(x\) が存在するような定数\(a\)の範囲を求めよ。
まずは、それぞれの不等式を解いて範囲を求めておきましょう。
これらの範囲を同時に満たすというのは、
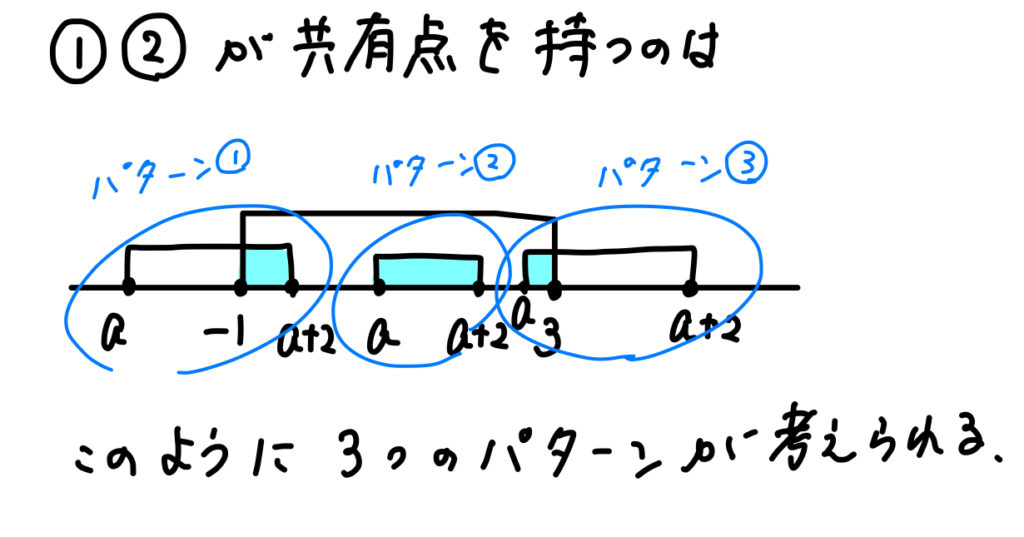
このように3つのパターンが考えられます。
しかし、これらをパターンごとに条件式を作っていくのはちょっと複雑で大変そうですよね(^^;)
なので一旦、「共有点を持たない」という逆を考えていくことにしましょう。
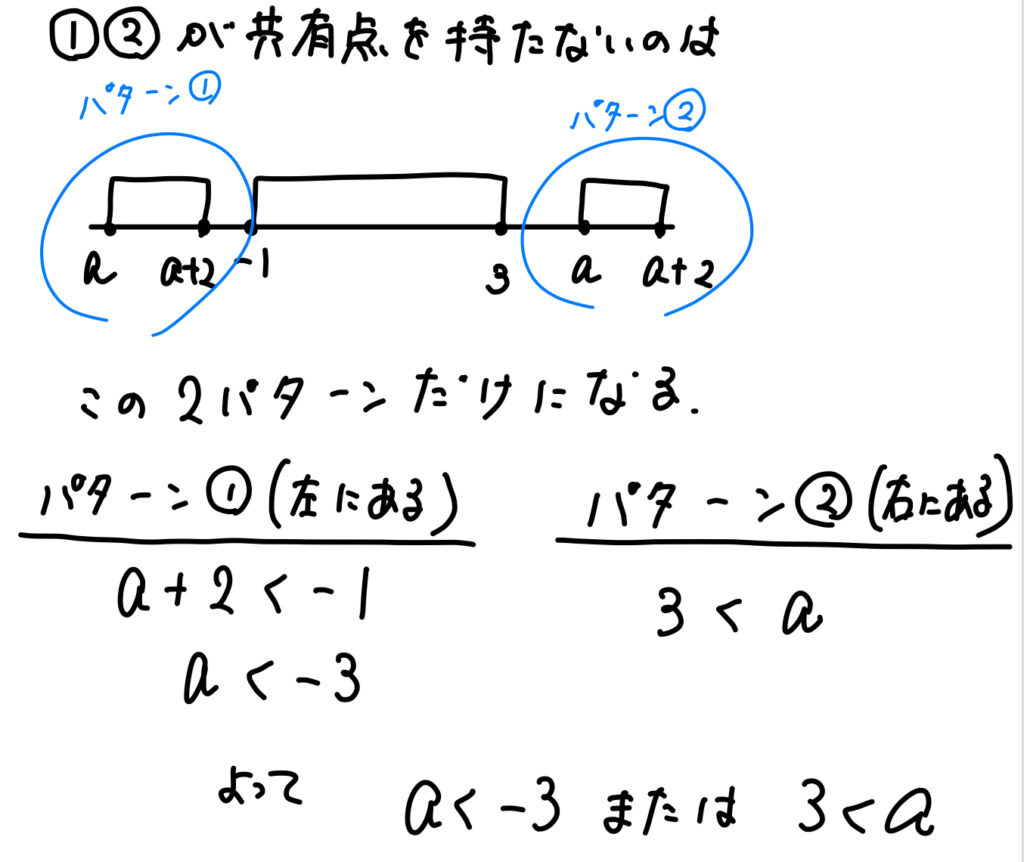
すると、共有点を持たないというのは、
このように2パターンしかなく、条件式も簡単に作ることができます。
共有点を持たない ⇒ \(a<-3\) または \(3<a\) ですので
共有点を持つのは、上記の範囲以外ということになり、
\(-3≦a≦3\) となります。
まとめ!
お疲れ様でした!
文字係数の2次不等式についての解説でしたが、
正直、この辺はちょっと難しいよね(^^;)
よくご質問をいただく問題でもあります。
ですが、ここの問題を理解して、サクサク解けるようにしておけば高得点、高偏差値を狙っていくことができるようになります。
なので、たくさん練習して理解を深めておきましょうね(/・ω・)/
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は?? ←今回の記事
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















コメントを残す