【反復試行の確率】数直線、点の移動を考えるサイコロ問題の解き方は？

今回は高校数学Aで学習する確率の単元から

『数直線上を点が移動する確率』

について解説していきます。

取り上げる問題はこちらだ！

今回の内容はこちらの動画でも解説しています！

数直線、点が動く確率の考え方と解き方！

5以上の目が出ると正の向きに2進む。

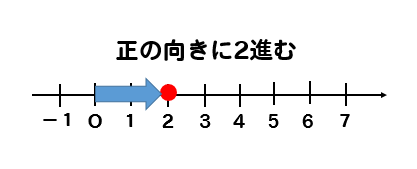
他の目が出ると負の向きに1進む。

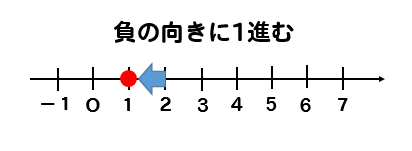
これを5回繰り返し

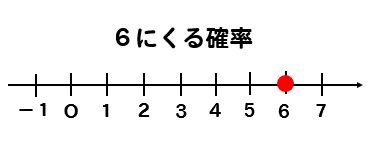
点Pが座標6の上にいる確率を考えたい。

これを解いていくためにはサイコロを6回投げたとき

5以上の目、他の目がそれぞれ何回ずつ出たのかを求める必要があります。

5以上の目が\(x\)回、他の目が\(y\)回出るとちょうど6の座標にくるとすると。

サイコロを合計で6回投げているので、\(x+y=6\)という式ができます。

更に

正の方向に2進むのが\(x\)回だから、\(+2x\)進んだことになり

負の方向に1進むのが\(y\)回だから、\(-y\)進んだことになります。

よって、合計で\(2x-y\)進むと表せます。

つまり、\(2x-y=6\)という式ができます。

以上より、連立方程式を用いて次のように表せます。

\begin{eqnarray} \left\{ \begin{array}{l} x + y = 6 \\ 2x – y = 6 \end{array} \right. \end{eqnarray}

この方程式を解くと

$$x=4,　y=2$$

ということが分かります。

つまり

5以上の目が4回

他の目が2回出れば点Pは6の場所にくるということが分かりました。

ここまで分かれば、あとは反復試行の公式に当てはめて考えていきます。

5以上の目が出る確率は、\(\displaystyle{\frac{1}{3}}\)であり

他の目が出る確率は、\(\displaystyle{\frac{2}{3}}\)であるから

$${}_6 \mathrm{ C }_4\left(\frac{1}{3}\right)^4\left(\frac{2}{3}\right)^2$$

$$=15\times  \frac{1}{81}\times \frac{4}{9}$$

$$=\frac{20}{243}$$

以上！

数直線を動く問題では、それぞれが何回ずつ動くのかを求める必要があります。

何回ずつ動くかが分かれば反復試行の公式に当てはめていけばOKです。

それでは、練習問題を通して理解を深めていきましょう。

練習問題で理解を深める！

まとめ！

お疲れ様でした！

数直線上を点が動く確率の問題では

この手順を踏めば簡単に求めることができますね(^^)

たくさん練習して、確実に解けるようにしておきましょう。

ファイトだ(/・ω・)/