今回は高校数学Ⅱで学習する内容から
『パスカルの三角形を用いて二項定理を考える』
という話を取り上げていきます。
パスカルの三角形というのは
こんな風に数がピラミッドのように並んでいるものでしたね。
それでは、このパスカルの三角形とはどのように数を並べていけば良いのか？
また、どんな場面で役に立つのでしょうか？
Contents
パスカルの三角形の作り方、覚え方！
それでは、パスカルの三角形を5段目まで作ってみましょう。
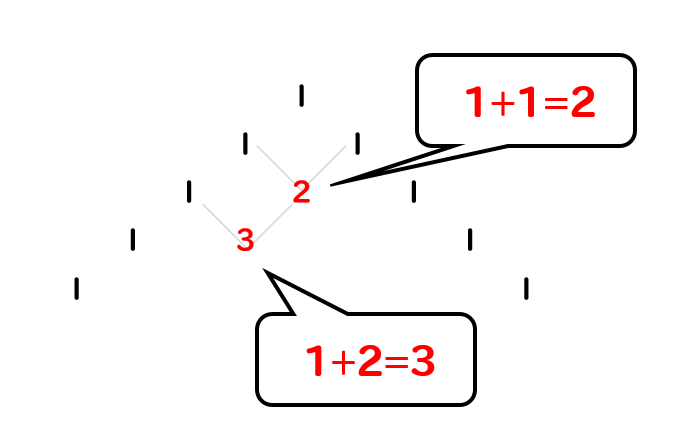
両端に１を書く
まずは、5段目まで両端に１を書いていきます。
間に数を埋める。
上の段にある数の間に、それぞれの数を足した値を書いていく。
完成！
これでパスカルの三角形は完成となります。
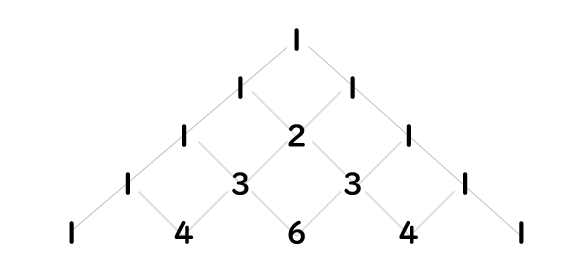
すごく簡単でしたね。
パスカルの三角形 作り方手順
- 各段の両端に１を書く
- 上の段にある数の間に和の値を書く
- 完成！
パスカルの三角形の使い道
それでは、このパスカルの三角形というものが
どういった場面で役に立つのか、それは…
展開公式の係数を調べることができる！
という点です。
例えば、\((a+b)^4\)の展開を考える場合
パスカルの三角形の5段目を見ると
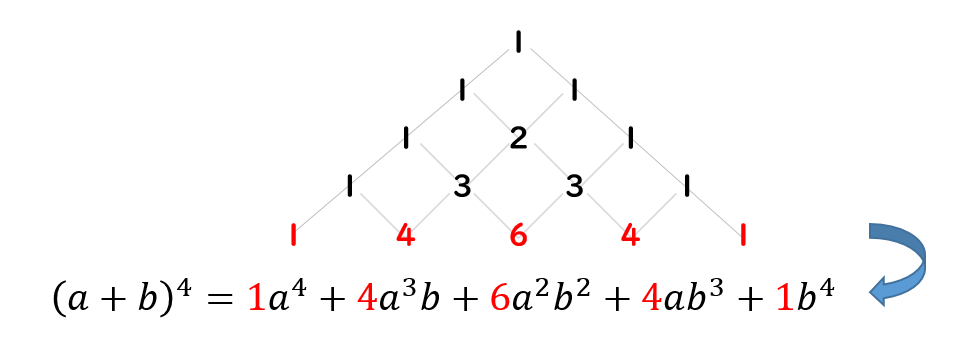
このように数が対応しているのです。
とっても便利ですね！！
パスカルの三角形を書くことで、複雑な展開公式であっても簡単に係数を調べてあげることができます。
それぞれこのように対応しています。
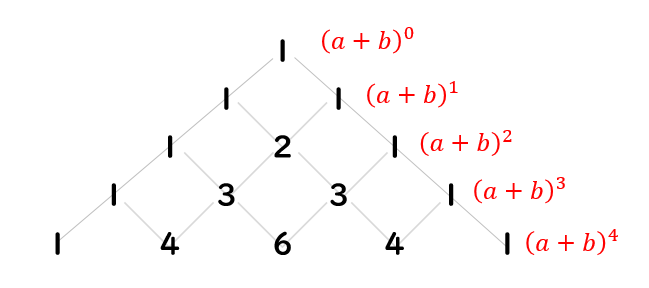
それでは、パスカルの三角形を使って展開の計算をやってみましょう！
練習問題に挑戦！
パスカルの三角形を用いて、次の展開式を求めよ。
$$(x+1)^5$$
$$(2x-1)^4$$
まとめ
パスカルの三角形が作れるようになると、展開公式を簡単に解けるようになりますね！
展開の計算で困ってしまったときには、ぜひとも利用してください(^^)
効率よく学習を進めていきたい方は必見！
この記事を通して、学習していただいた方の中にはもっといろんな単元の学習を進めていきたい！
という素晴らしい学習意欲を持っておられる方もいる事でしょう。
だけど
どこの単元を学習すればよいのだろうか。
何を使って学習すればよいのだろうか。
勉強を頑張りたいけど 何をしたらよいか悩んでしまって
手が止まってしまう…
そんなお悩みをお持ちの方もおられるのではないでしょうか。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで
どの単元を学習すればよいのか 何を解けばよいのか
そういった悩みを全て解決することができます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
スタディサプリ 7つのメリット
- 費用が安い！月額1980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
今までの悩みを解決し、効率よく学習を進めていきましょう。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
数スタの公式LINEを開設しました！