和差算とは、数量の和や差が分かっているとき、それぞれの数がどうなっているのかを求める計算です。
どんな問題なのかというと
こんな感じ！
んー、ややこしいっていうか。
どうやって求めるん！？って感じだねｗ
今回の記事では、和差算の解き方、考え方について例題を使って説明していきます。
【和差算とは】解き方、考え方を解説！
それでは、先ほどの問題の解き方について説明していきます。
AくんとBくんの持っている金額は合わせて800円。AくんはBくんよりも140円多く持っています。2人が持っている金額は、それぞれいくらか求めましょう。
AくんとBくんの合計が800円。
Aくんの方がBくんよりも140円多いということで
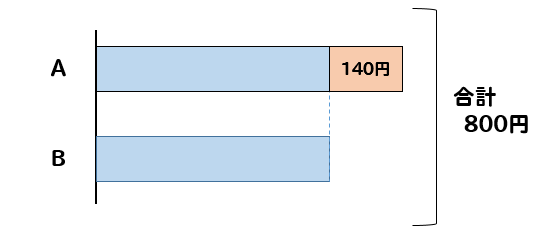
イメージとしてはこんな感じだね。
それでは、この状態からAくんの140円を取り除いたらどうなるでしょうか。
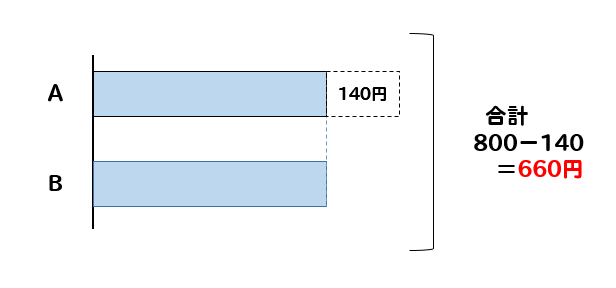
AくんとBくんの持っている金額が等しくなり、合計は140円だけ少なくなり660円となります。
このとき、2人の持っている金額は等しいから
$$660\div2=330円$$
このように合計金額を半分にすることでBくんが持っている金額を求めることができます。
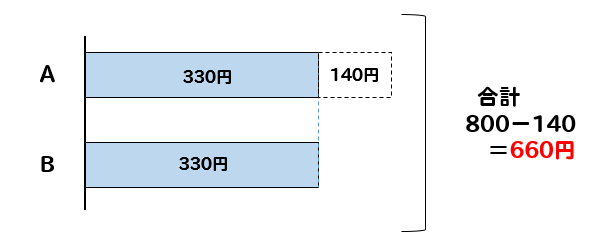
すると、Aくんの持っていた金額は
$$330+140=470円$$
ということが分かりますね！
答え
Aくん：470円 Bくん：330円
これが和差算の考え方です。
多い方から差の分を取り除き、それぞれを同じ数にする。
そのときの合計から、小さい方の数を求めることができる。
この考え方を思いつくのは難しいですが、知ってしまえば利用することは簡単です(^^)
それでは、サクッと練習問題に挑戦してみましょう。
練習問題に挑戦！
【和差算とは】比べる数が多い場合の例題！
A、B、Cの3人で、900円を次のように分けました。AはBよりも15円多く、CはBより20円少ない。このとき、3人はそれぞれ何円ずつ受け取ったか求めましょう。
比べる数が増えたとしても、考え方は同じです。次のイメージ図を見ながら考えてみましょう。
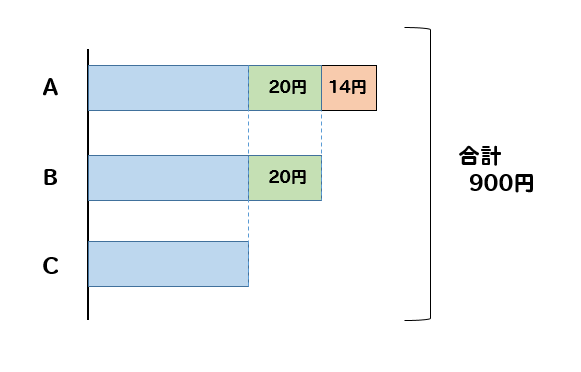
一番少ないCを基準として、AとBの多くなっている部分を取り除いてしまいます。
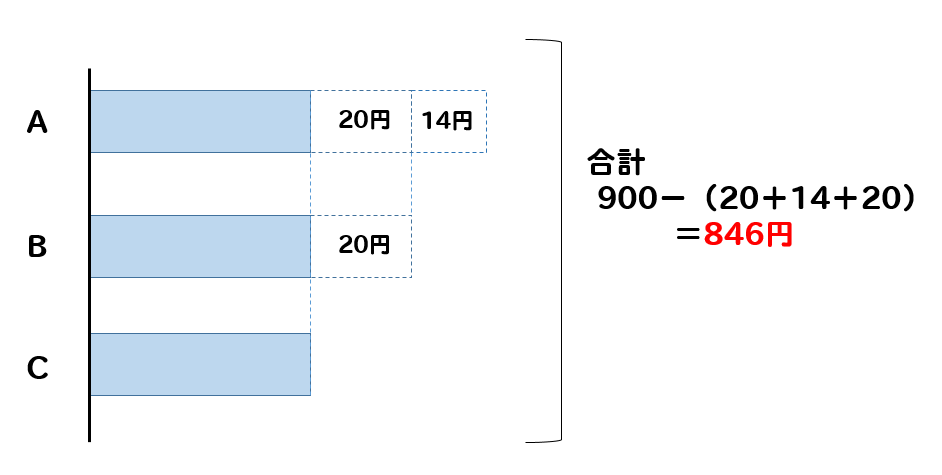
すると、Aからは34円、Bからは20円が取り除かれます。
よって、合計金額は54円だけ取り除かれ、846円となります。
あとは、これを3等分することで一番少なかったCの金額を求めることができます。
$$846\div 3=282円$$
A、BはCの金額を元にしてそれぞれ次のように求めることができます。
Aの金額は
$$282+(20+14)=316円$$
Bの金額は
$$282+20=302円$$
答え
A：316円 B：302円 C：282円
今回の場合も、基準を作って差の分だけ取り除く！
これが解き方のポイントになりますね(^^)
それでは、理解を深めるためにサクッと練習問題に挑戦してみましょう。
練習問題に挑戦！
【和差算とは】考え方、解き方まとめ！
お疲れ様でした！
考え方が分かれば、問題を解くのは簡単でしたね(^^)
一番小さい数に基準を揃えて、大きい数から差の文だけ取り除く。
そこから、等分して基準の数を見つける！
これが和差算の考え方、解き方でした。
あとはいろんな問題に挑戦し、理解を深めていきましょう。
中学受験に必須な特殊算を学びたいなら
植木算、和差算、消去算、つるかめ算、過不足算、方陣算、旅人算、損益算、濃度算、日暦算、相当算、還元算、平均算、仕事算、倍数算、ニュートン算、流水算、通過算、時計算
中学受験を乗り切るためには、こんなにもたくさんの特殊算を身につけなければいけません。
しかも、学校学習の中では教えてくれないものばかり。
塾に通えない子供たちは独学で学習していかなければなりません。
これは正直、かなりキツイ…
だから、スタディサプリを使ってサクッと身につけてしまいましょう。
上で紹介した特殊算を１から丁寧に解説、そして演習問題で理解を深めることができます。
中学受験を乗り切るため、特殊算を身につけたいならスタディサプリが利用してみましょう！
これからは聴いて学ぶ時代！？
Audibleで世界が変わった！これからは音声で勉強する時代へ！？
2018.11.10