【算数】場合の数の解き方は？問題別に考え方を解説！

今回は、小学生で学習する『場合の数』の問題について解説していくよ！

 

問題のパターン別に解説していくので、それぞれの問題での考え方解き方をしっかりと身につけていこう！

 

順番を考える場合の数

 

順番を考えるときには樹形図を使って考えていきましょう！

まず、Aが先頭になる並び方から考えてみましょう。

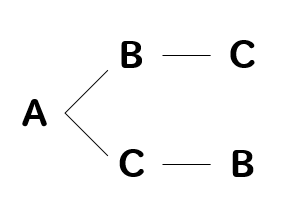
すると、このように

ABC、ACBと2通りの並べ方があることがわかりますね。

よって、（1）の答えは2通りとなります。

 

次に、全体を考えていきます。

Aを先頭にして並べる方法が2通りでした。

ということは同じように考えて

Bを先頭にした場合も2通り

Cを先頭にした場合も2通りあると考えることができます。

 

よって、全体は

となります。

 

全体の場合の数を考える場合には

いちいち樹形図を書いていると手間になってしまいます。

今回のように、先頭を１つ固定した場合の樹形図を書いて、そこから全体を計算していくと簡単に求めることができますよ＾＾

 

 

 

数字を並べて整数を作る場合の数

 

こちらの問題も先ほどと同様、先頭にくる数を固定して考えてみましょう。

まずは、１が先頭にくる場合を樹形図を使って考えると

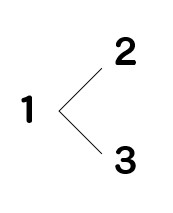
12、13という2通りの2けたの数を作ることができます。

同じように２、３が先頭の場合にも2通り。

 

よって

$$3\times 2=6通り$$

ということが分かりますね＾＾

 

 

先ほどと同じような問題に見えますが、ちょっと注意したいことがあります。

それは、０が含まれていること！

０は先頭に持ってくることができません！

だって、０が先頭になると２けたではなくなっちゃうもんね。

 

それでは、０に注意して考えていきましょう。

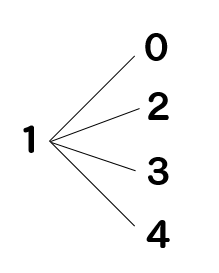
１を先頭にした場合

10、12、13の3通りの数を作ることができます。

同じように先頭が２，３のときも3通りできるので

$$3\times 3=9通り$$

となります。

先頭に持ってこれる数が１、２、３の3通りしかないことに注意ですね！

 

 

 

組み合わせを考える場合の数

 

今回は、組み合わせを考える問題となっています。

つまり、ペアを作るということなので

AとBを選んだ場合とBとAを選んだ場合は、それぞれ同じものだとして考えます。

 

だって、AとBがいるグループとBとAがいるグループ

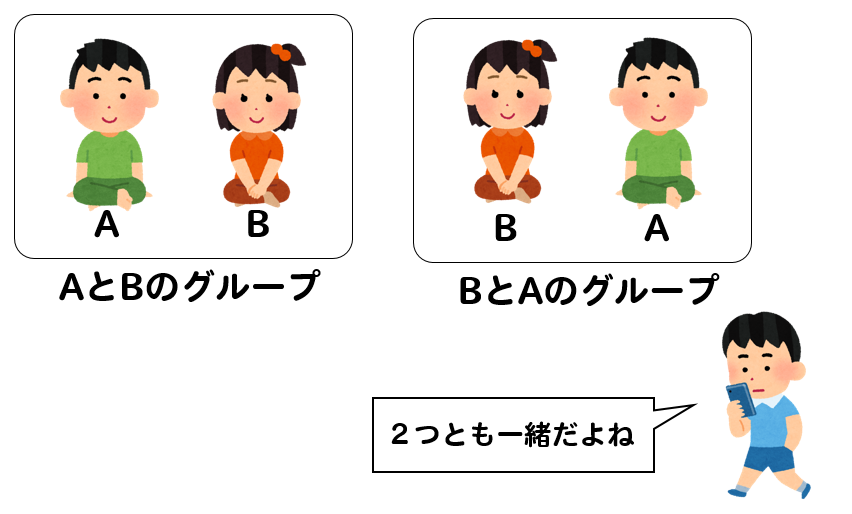
それぞれ中身は同じだもんね。

ペアを作るという場合の数においては、このように順番は関係ありません。

そこに注意して考えていきましょう。

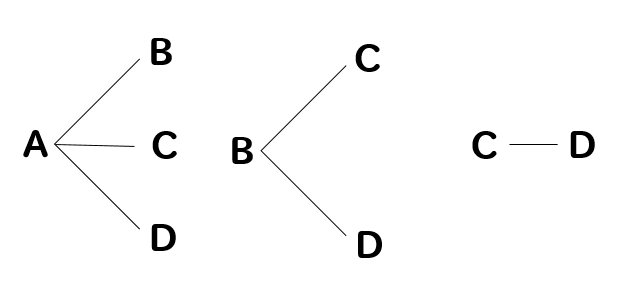
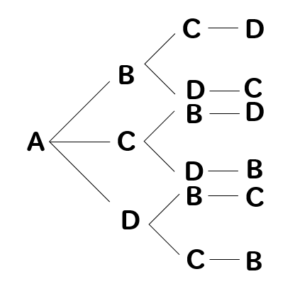
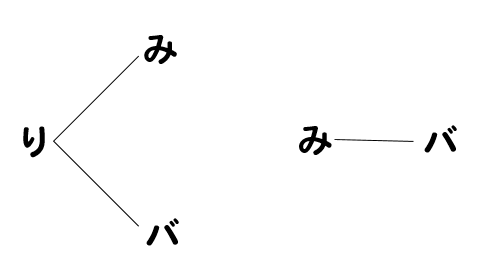
すると、樹形図はこんな感じになります。

逆にしただけのものは、省いていくから少しずつ減っていく形になっちゃうね。

よって、全部で6通りということになります。

 

 

 

似た問題なんだけど、注意したいのが次。

 

今回も選ぶという問題なので、さっきと同じように考えてしまいがちです。

しかし、選ばれた2人には委員長と副委員長という役職がついています。

 

つまり

AとBが選ばれた場合でも

Aが委員長、Bが副委員長

Bが委員長、Aが副委員長

という2通りのパターンが考えられます。

 

よって、この問題では

AとB、BとAは別物として考えていきます。

そのため、樹形図ではこんな感じ。

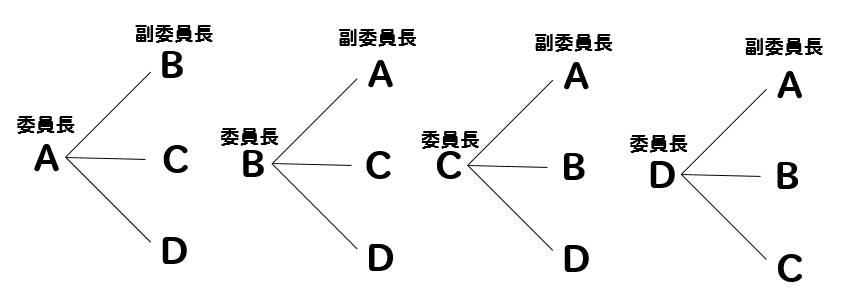
全部で12通りあることが分かります。

 

 

 

問題文に「選ぶ」という言葉があれば必ず組み合わせ！とは限りません。

問題をよく読んで

AとB、BとAそれぞれ入れ替えても同じだ！と考えられるなら組み合わせ。

入れ替えると違うものだ！と考えられるなら順番を数えるときと同じように求めてください！

 

 

対戦回数を考える場合の数

 

総当たり戦の試合をするとき、全部で何試合行われるかを考える問題です。

ちょっと難しいように思えますが、考え方はシンプルです。

先ほど考えた、ペアを作る問題と同じように考えていきましょう。

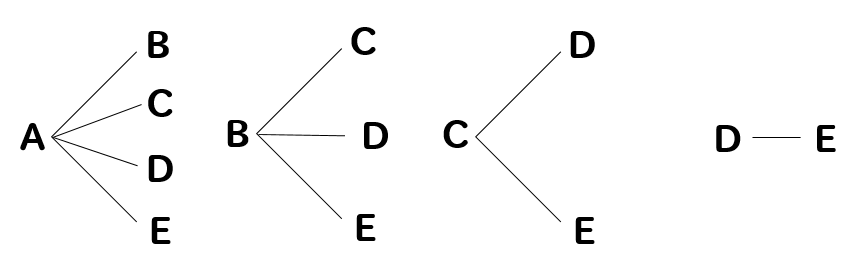
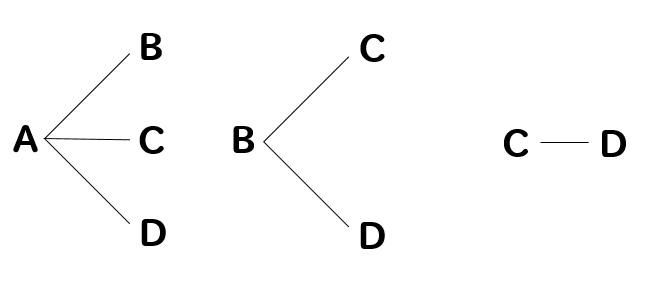
樹形図を使って考えると、このように10通りということが分かりますね(^^)

 

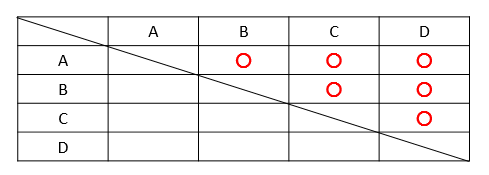
対戦表のように、表を使って考えると

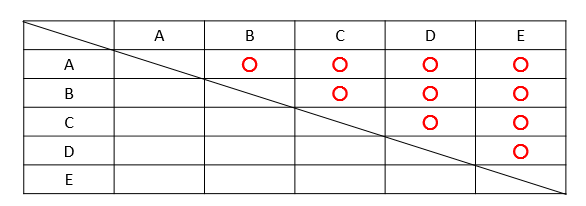
このように全部で10試合あるっていうことが読み取れますね。

 

 

選ばない！？場合の数

 

3人を選ぶ！？

そんなのどうやって樹形図書くんだろう…と困ってしまいますが発想を転換してみましょう。

 

4人の中から3人を選ぶというのは

見方を変えると『1人選ばれない』ということですよね。

（1人だけ選ばれないなんて、かわいそう…）

 

つまり

Aが選ばれない＝B、C、Dが選ばれる

Bが選ばれない＝A、C、Dが選ばれる

Cが選ばれない＝A、B、Dが選ばれる

Dが選ばれない＝A、B、Cが選ばれる

の全部で4通りあることがわかります。

 

このように、問題の見方を変えることで簡単に解くことができる場合もあります(^^)

 

 

まとめ

お疲れ様でした！

今回は、小学校で学習する場合の数について問題解説をしていきました。

 

習ったばかりの頃は、樹形図を書くのにも一苦労すると思いますが、とにかく練習あるのみです！

中学でも同じような問題を学習することになるので、今のうちにしっかりと理解を深めておくことが大切です(^^)

 

ファイトだー(/・ω・)/