今回は、旅人算とよばれる問題の中から
往復するときは？2回目に出会うのは？
というパターンの解き方について解説していきます。
ちょっと変わった視点で解いていく問題なので、解答を見ても…
？？
となってしまう方も多いようです(^^;)
この記事では、なるべーく丁寧に説明をつけていきますので、１つ１つ理解していきましょう。
Contents
【旅人算】往復するときの解き方は？
往復をして2人が初めて出会うときを考えると
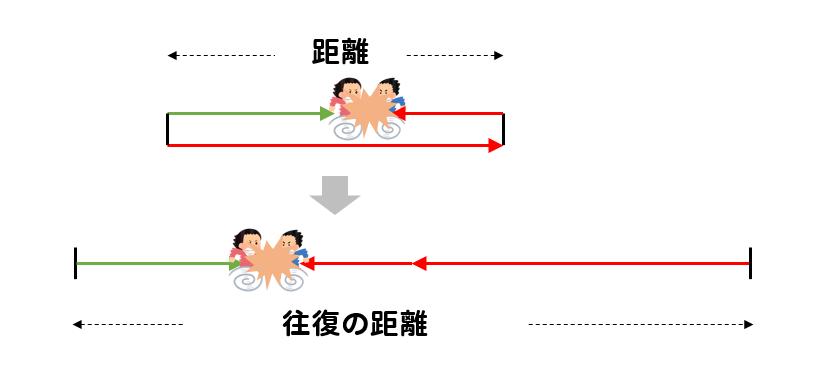
このようなイメージになります。
つまり、2人が進んできた道のりを合わせると往復の道のりに等しくなる。
ということです。
この問題において、往復の距離とは
$$1650\times 2=3300m$$
のことですね。
つまり、2人が出会うというのは、2人の進んできた道のりの合計が3300mになったときということです。
では次に、2人はどれくらいのペースで進んでいっているのかを考えます。
AくんとBさんが出発してから1分後の状況を考えてみましょう。
Aくんは分速60mだから、60m進んでおり
Bさんは分速50mだから、50m進んでいます。
つまり、1分後には2人合わせて110m進んだことになります。
ということは！
2人が合わせて3300m進むためには
$$3300\div 110=30分$$
30分の時間がかかるということが求まりました。
よって、2人が出会うのは出発してから30分後となります。
このような手順で求めていきましょう(^^)
ポイントとしては、往復して2人が出会うまでに進んできた道のりが往復の距離と等しくなっていること。
そして、2人が1分間に合わせてどれくらいのペースで進んでいるのかを求めることです。
では、サクッと練習問題を解いてみましょう。
練習問題に挑戦！
【旅人算】往復、2回目に出会うときの解き方は？
なんじゃこりゃ、ややこしいな…って感じですが、落ち着いて考えていきましょう(^^;)
まず！
お互い、別々の場所から反対方向に向かって進んでいるので初めて出会うというのは次のようなシチュエーションになります。
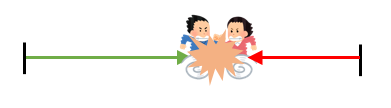
そして、2回目に出会うというのは次のようなシチュエーションになります。
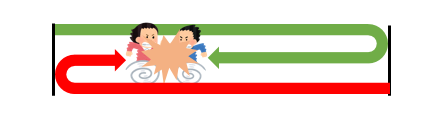
これを引き延ばして考えてみると
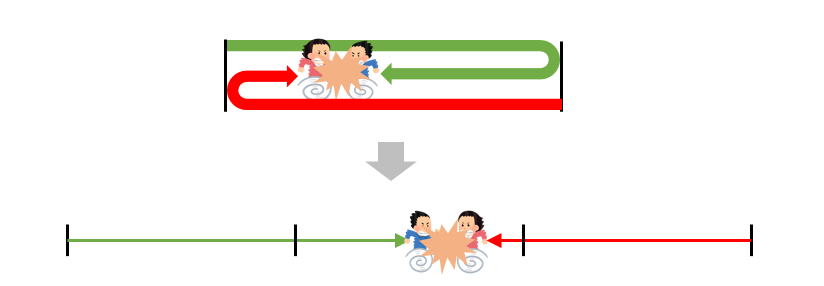
このように、2人の進んできた道のりの合計が家と駅までの3倍になっていることが分かります。
つまり、2人の進んだ道のりの合計が \(12\times 3=36km\) になったとき、2人は2回目に出会うということになります。
2人は1時間にそれぞれ6㎞、4㎞ずつ進むことから2人合わせると10㎞ずつ進むということが分かります。
よって
$$36\div10=3.6時間$$
2人が2回目に出会うのは3.6時間後ということが求まりました。
これを時間と分に分けて考えると
$$3.6時間=3時間36分$$
となりました。
この問題でのポイントは、2人が2回目に出会うまでに進んできた道のりの合計がどれくらいになっているのかを考えることです。
頭の中ではイメージしづらいと思うので、迷ったら絵に書いてみるといいですね！
では、サクッと練習問題に挑戦してみましょう。
練習問題に挑戦！
【旅人算】往復、2回目に出会うときの問題まとめ！
お疲れ様でした！
往復を考える問題では、頭の中でのイメージが難しい…
なので、迷ったときには絵を描いて、2人が進んできた道のりがどういった値になっているのかを考えることが大事です。
たくさん練習して理解を深めておきましょう！
また、旅人算には他にもたくさんのパターンの問題があります。
- 2人が出会う
- 2人が追いつく
- 池の周りを回る
- 往復する
他のパターンについては、こちらの記事でまとめているのでご参考ください。
中学受験に必須な特殊算を学びたいなら
植木算、和差算、消去算、つるかめ算、過不足算、方陣算、旅人算、損益算、濃度算、日暦算、相当算、還元算、平均算、仕事算、倍数算、ニュートン算、流水算、通過算、時計算
中学受験を乗り切るためには、こんなにもたくさんの特殊算を身につけなければいけません。
しかも、学校学習の中では教えてくれないものばかり。
塾に通えない子供たちは独学で学習していかなければなりません。
これは正直、かなりキツイ…
だから、スタディサプリを使ってサクッと身につけてしまいましょう。
上で紹介した特殊算を１から丁寧に解説、そして演習問題で理解を深めることができます。
中学受験を乗り切るため、特殊算を身につけたいならスタディサプリが利用してみましょう！
これからは聴いて学ぶ時代！？
Audibleで世界が変わった！これからは音声で勉強する時代へ！？
2018.11.10